Xác định Các Hệ Số A B C để Hàm Số Y=ax2 Bx C Có Giá Trị Nhỏ Nhất ...

Học liệu Hỏi đáp Đăng nhập Đăng ký

• Học bài
• Hỏi bài
• Kiểm tra
• ĐGNL
• Thi đấu
• Thư viện số
• Bài viết Cuộc thi Tin tức Blog học tập
• Trợ giúp
• Về OLM

(Từ ngày 12/12) Lớp live ôn thi cuối kỳ I hoàn toàn miễn phí - Tham gia ngay!!!

 Mở bộ đề mới - nhận quà VIP liền tay

• Mẫu giáo
• Lớp 1
• Lớp 2
• Lớp 3
• Lớp 4
• Lớp 5
• Lớp 6
• Lớp 7
• Lớp 8
• Lớp 9
• Lớp 10
• Lớp 11
• Lớp 12
• ĐH - CĐ

K Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác nhận câu hỏi phù hợp

×

Chọn môn học Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên Mua vip

• Tất cả
• Mới nhất
• Câu hỏi hay
• Chưa trả lời
• Câu hỏi vip

L lyletrung 6 tháng 10 2016 - olm

Xác định các hệ số a b c để hàm số y=ax2+bx+c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng 1 khi x =1

#Hỏi cộng đồng OLM #Toán lớp 9 1 L lyletrung 6 tháng 10 2016

Giúp với ạ gắp lắm :(

Đúng(0) PT Pham Trong Bach 14 tháng 9 2017 Xác định parabol (P) ; y= ax2+bx+ c biết: Hàm số y= ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng  khi x=1. A. y= x2+ x+1. B. y=- x2-x+1. C. y= -x2-x-1. D. y= x2-x+1...Đọc tiếp

Xác định parabol (P) ; y= ax2+bx+ c biết: Hàm số y= ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng  khi x=1.

A. y= x2+ x+1.

B. y=- x2-x+1.

C. y= -x2-x-1.

D. y= x2-x+1

#Hỏi cộng đồng OLM #Toán lớp 10 1 CM Cao Minh Tâm 14 tháng 9 2017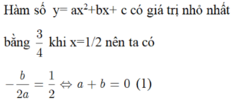

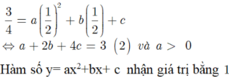
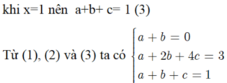
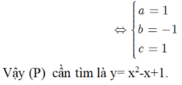
Chọn D.

Đúng(1) PT Pham Trong Bach 24 tháng 3 2019 Xác định parabol (P): y = a x 2 + bx + c, a ≠ 0 biết hàm số có giá trị nhỏ nhất bằng  3 4  khi x= 1 2   và nhận giá trị bằng 1 khi x = 1. A. y = − x 2 + x + 1 B. y =  x 2 + x – 1  C. y = x ...Đọc tiếp

Xác định parabol (P): y = a x 2 + bx + c, a ≠ 0 biết hàm số có giá trị nhỏ nhất bằng  3 4  khi x= 1 2   và nhận giá trị bằng 1 khi x = 1.

A. y = − x 2 + x + 1

B. y =  x 2 + x – 1 

C. y = x 2   - x + 2 

D. y = x 2 - x + 1 

#Hỏi cộng đồng OLM #Toán lớp 10 1 CM Cao Minh Tâm 24 tháng 3 2019

Đáp án D

Đúng(0) PT Pham Trong Bach 1 tháng 7 2017 Tìm a, b, c sao cho hàm số y = x 3 + a x 2 + b x + c có giá trị bằng 0 khi x = 1 và đạt cực trị khi bằng 0 khi x = -1 . A. a   =   - 1 ;   b   =   1 ;   c   =   ...Đọc tiếp

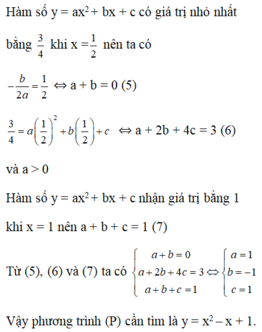
Tìm a, b, c sao cho hàm số y = x 3 + a x 2 + b x + c có giá trị bằng 0 khi x = 1 và đạt cực trị khi bằng 0 khi x = -1 .

A. a   =   - 1 ;   b   =   1 ;   c   =   1

B.  a   =   - 1 2 ;   b   =   - 1 ;   c   =   - 1 2

C.  a   =   1 ;   b   =   - 1 ;   c   = - 1

D.  a   =   1 2 ;   b   =   - 1 ;   c   =   1 2

#Hỏi cộng đồng OLM #Toán lớp 12 1 CM Cao Minh Tâm 1 tháng 7 2017

Sử dụng giả thiết và điều kiện cần của cực trị ta có

y(1) = 0; y'(-1) = 0; y(-1) = 0

Trong đó ,  y ' = 3 x 2 + 2 a x + b

Từ đó suy ra:

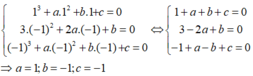
Với a = 1; b = -1; c = -1 thì hàm số đã cho trở thành  y = x 3 + x 2 - x - 1

Ta có y ' = 3 x 2 + 2 x - 1 , y ' ' = 6 x + 2 . V ì y ' ' = ( - 1 ) = - 4 < 0  nên hàm số đạt cực đại tại x = -1 . Vậy a = 1; b = -1; c = -1 là các giá trị cần tìm.

Chọn đáp án C.

Đúng(0) DH Đỗ hải 31 tháng 12 2020 Xác định hàm số a b c để hs y=ax^+bx+c =0 có giá trị nhỏ nhất -4/3 khi x= 1/3 và đồ thị hs đi qua điểm A(2;7) #Hỏi cộng đồng OLM #Toán lớp 10 1 NN Nguyễn Ngọc Lộc 31 tháng 12 2020

- Từ các giả thiết của đề bài ta có hệ phương trình :

\(\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\-\dfrac{b}{2a}=\dfrac{1}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\2a+3b=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-2\\c=-1\end{matrix}\right.\)

Vậy hàm số trên có dạng : \(3x^2-2x-1=0\)

Đúng(1) DA Đức Anh Trần 22 tháng 12 2021

Tính a2 + b2 + c2 biết hàm số y = ax2 + bx +c  (a khác 0) đạt giá trị nhỏ nhất bằng -1/4 khi x = 5/2 và đồ thị cắt trục Ox tại hai điểm sao cho tích hai hoành độ bằng 6

#Hỏi cộng đồng OLM #Toán lớp 10 0 QT Quoc Tran Anh Le CTVVIP 24 tháng 9 2023

Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)

a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)

b) Xác định tập giá trị và khoảng biến thiên của hàm số.

#Hỏi cộng đồng OLM #Toán lớp 10 1 KS Kiều Sơn Tùng 24 tháng 9 2023

Tham khảo:

a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)

Lại có:

 \(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)

\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)

Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))

Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)

b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)

Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)

Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)

Hay \(S\left( {0;1} \right).\)

Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)

Đúng(0) BN bảo nguyễn 11 tháng 3 2023 xác định hàm số bậc 2 có đồ thị là parabol (p) biết : a, (P) : y= ax^2 + bx + c có giá trị lớn nhất bằng 1 khi x = 2, đồng thời (P) qua M( 4; -3) #Hỏi cộng đồng OLM #Toán lớp 10 1 NV Nguyễn Việt Lâm 11 tháng 3 2023

Với \(a\ne0\) từ đề bài ta có:

\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a+b=0\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\)

\(\Rightarrow a=-1;b=4;c=-3\)

Vậy (P): \(y=-x^2+4x-3\)

Đúng(2) PT Pham Trong Bach 12 tháng 7 2018 a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)Tính tọa độ giao điểm A và B của (C1) và (C2).c. Tính các hệ số a, b, c để hàm số y = ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và...Đọc tiếp

a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)

b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)

Tính tọa độ giao điểm A và B của (C1) và (C2).

c. Tính các hệ số a, b, c để hàm số y = ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.

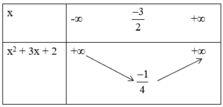
#Hỏi cộng đồng OLM #Toán lớp 10 1 CM Cao Minh Tâm 12 tháng 7 2018

a) f(x) = 2x.(x+2) - (x+2)(x+1) = 2x2 + 4x - (x2 + 3x + 2) = x2 + x - 2

Tam thức x2 + x – 2 có hai nghiệm x1 = -2 và x2 = 1, hệ số a = 1 > 0.

Vậy:

+ f(x) > 0 nếu x > x2 = 1 hoặc x < x1 = -2, hay x ∈ (-∞; -2) ∪ (1; + ∞)

+ f(x) < 0 nếu x1 < x < x2 hay x ∈ (-2; 1)

+ f(x) = 0 nếu x = -2 hoặc x = 1.

b)

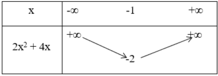
* Hàm số y = 2x(x+2) = 2x2 + 4x có đồ thị (C1) là parabol có:

+ Tập xác định: D = R

+ Đỉnh I1( -1; -2)

+ Trục đối xứng: x = -1

+ Giao điểm với trục tung tại gốc tọa độ.

+ Giao điểm với trục hoành tại O(0; 0) và M(-2; 0).

+ Bảng biến thiên:

* Hàm số y = (x + 2)(x+1) = x2 + 3x + 2 có đồ thị (C2) là parabol có:

+ Tập xác định D = R.

+ Đỉnh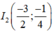 

+ Trục đối xứng: x = -3/2

+ Giao với trục tung tại D(0; 2)

+ Giao với trục hoành tại M(-2; 0) và E(-1; 0)

+ Bảng biến thiên

* Đồ thị:

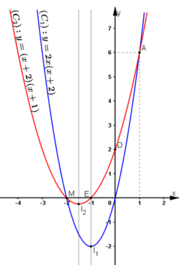
* Tìm tọa độ giao điểm:

Cách 1: Dựa vào đồ thị hàm số:

Nhìn vào đồ thị thấy (C1) cắt (C2) tại A(1; 6) và B ≡ M(-2; 0)

Cách 2: Tính:

Hoành độ giao điểm của (C1) và (C2) là nghiệm của phương trình:

2x(x + 2) = (x + 2)(x + 1)

⇔ (x + 2).2x – (x + 2)(x + 1) = 0

⇔ (x + 2).(2x – x – 1) = 0

⇔ (x + 2).(x – 1) = 0

⇔ x = -2 hoặc x = 1.

+ x = -2 ⇒ y = 0. Ta có giao điểm B(-2; 0)

+ x = 1 ⇒ y = 6. Ta có giao điểm A(1; 6).

c)

+ Đồ thị hàm số y = ax2 + bx + c đi qua điểm A(1; 6) và B(-2; 0)

⇔ tọa độ A và B thỏa mãn phương trình y = ax2 + bx + c

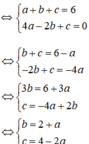
+ Ta có bảng biến thiên của hàm số y = ax2 + bx + c:

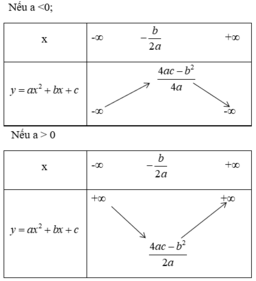
Nhận thấy y đạt giá trị lớn nhất bằng 8

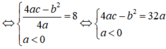
Thay b = 2 + a và c = 4 – 2a vào biểu thức 4ac – b2 = 32a ta được:

4.a.(4 – 2a) – (2 + a)2 = 32a

⇔ 16a – 8a2 – (a2 + 4a + 4) = 32a

⇔ 16a– 8a2 – a2 – 4a - 4 – 32a = 0

⇔ -9a2 - 20a - 4 = 0

⇔ a = -2 hoặc a = -2/9.

Nếu a = -2 ⇒ b = 0, c = 8, hàm số y = -2x2 + 8

Nếu a = -2/9 ⇒ b = 16/9, c = 40/9, hàm số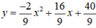 

Đúng(1) NT Nguyễn Thị Phương 1 tháng 11 2021 - olm

Xác định Parabol (P) : y = ax^2 + bx + c ( a khác 0 ) biết (P) đi qua :

a, điểm E (0; 6) và hàm số y = ax^2 - bx + c đạt giá trị nhỏ nhất là 4 khi x = -2

b, điểm F (1; 16) và cắt Ox tại các điểm có hoành độ là -1 và 5.

#Hỏi cộng đồng OLM #Toán lớp 10 0 Xếp hạng Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên

• Tuần
• Tháng
• Năm

• E ✦𝘉é✿𝘤𝘩í𝘱✦ 4 GP
• E ElmSunn 4 GP
• 0D 𓃱⋆⭒˚.⋆🪐ºҩº☞†®üñɕ-đẹρ-†®åî⋆⭒˚.⋆ VIP 4 GP
• NT Nguyễn Trọng Đạt VIP 4 GP
• TL Truong Lan VIP 4 GP
• D Đ𝙖̆𝙣𝙜 𝙈𝙞𝙣𝙝 (𝙈𝙚𝙤𝙠𝙤𝙣𝙝𝙤𝙣𝙜𝙪𝙤𝙣𝙜𝙩𝙝𝙪𝙤𝙘) 4 GP
• NV ✫⊰ Ngô Vũ ༒ Công Vinh ⊱✫ VIP 4 GP
• NB Nguyễn Bá Hiếu 4 GP
• KV Kiều Vũ Linh 2 GP
• SV Sinh Viên NEU 2 GP

Học liệu Hỏi đáp Link rút gọn Link rút gọn Để sau Đăng ký

Các khóa học có thể bạn quan tâm

× Mua khóa học Tổng thanh toán: 0đ (Tiết kiệm: 0đ) Tới giỏ hàng Đóng ×

Yêu cầu VIP

×

Học liệu này đang bị hạn chế, chỉ dành cho tài khoản VIP cá nhân, vui lòng nhấn vào đây để nâng cấp tài khoản.