Xác định Hàm Số Bậc Hai Y = Ax2 Bx C Có đồ Thị Là Parabol (P ... - Hoc24
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
 Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay trần trang 3 tháng 12 2019 lúc 19:01
trần trang 3 tháng 12 2019 lúc 19:01 Xác định hàm số bậc hai y = ax2 + bx + c có đồ thị là parabol (P) nhận đường thẳng x = 2 làm trục đối xứng và đi qua các điểm M(1;0) và N(4;-3)
Lớp 10 Toán Ôn tập chương II Những câu hỏi liên quan
- Pham Trong Bach
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Đi qua hai điểm A(3; -4) và có trục đối xứng là x = -3/2
Xem chi tiết Lớp 10 Toán 1 1 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  14 tháng 5 2017 lúc 9:38
14 tháng 5 2017 lúc 9:38 + Parabol y = ax2 + bx + 2 có trục đối xứng x = –3/2
⇒ –b/2a = –3/2 ⇒ b = 3a (1)
+ Parabol y = ax2 + bx + 2 đi qua điểm A(3; –4)
⇒ –4 = a.32 + b.3 + 2 ⇒ 9a + 3b = –6 (2).
Thay b = 3a ở (1) vào biểu thức (2) ta được:
9a + 3.3a = –6 ⇒ 18a = –6 ⇒ a = –1/3 ⇒ b = –1.
Vậy parabol cần tìm là y = –1/3x2 – x + 2.
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Nguyễn Huyền
 Gửi Hủy
Gửi Hủy 
- dũng nguyễn tiến
xác định hàm số bậc hai ax2+bx+c biết rằng đồ thị hàm số là parabol đi qua điểm B<0,4> và có đỉnh I <1,5>
Xem chi tiết Lớp 10 Toán §3. Hàm số bậc hai 1 0
 Gửi Hủy
Gửi Hủy  Nguyễn Lê Phước Thịnh CTV
Nguyễn Lê Phước Thịnh CTV  18 tháng 12 2021 lúc 21:06
18 tháng 12 2021 lúc 21:06 Theo đề, ta có: c=4
Theo đề, ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=1\\-\dfrac{b^2}{16a}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2+80a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-20\\b=40\end{matrix}\right.\)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Bài 6.31
-
Xác định parabol \(\left( P \right):y = a{x^2} + bx + 3\) trong mỗi trường hợp sau:
a) \(\left( P \right)\) đi qua hai điểm \(A(1;1)\) và \(B( - 1;0)\).
b) \(\left( P \right)\) đi qua điểm \(M(1;2)\) và nhận đường thẳng \(x = 1\) làm trục đối xứng.
c) \(\left( P \right)\) có đỉnh là \(I(1;4).\)
Xem chi tiết Lớp 10 Toán Bài tập cuối chương VI 1 0 Gửi Hủy
Gửi Hủy  Hà Quang Minh Giáo viên CTVVIP
Hà Quang Minh Giáo viên CTVVIP  30 tháng 9 2023 lúc 23:42
30 tháng 9 2023 lúc 23:42 a) Theo giả thiết, hai điểm \(A(1;1)\) và \(B( - 1;0)\) thuộc parabol \(\left( P \right):y = a{x^2} + bx + 3\) nên ta có: \(\left\{ {\begin{array}{*{20}{c}}{a + b + 3 = 1}\\{a - b + 3 = 0}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = \frac{{ - 5}}{2}}\\{b = \frac{1}{2}}\end{array}} \right.} \right.\)
Vậy hàm số cần tìm là: \(y = - \frac{5}{2}{x^2} + \frac{1}{2}x + 3.\)
b) Parabol nhận \(x = 1\) làm trục đối xứng nên \( - \frac{b}{{2a}} = 1\,\, \Leftrightarrow \,\,b = - 2a.\)
Điểm \(M(1;2)\) thuộc parabol nên \(a + b + 3 = 2\,\, \Leftrightarrow \,\,a + b = - 1.\)
Do đó, ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{b = - 2a}\\{a + b = - 1}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = - 2}\end{array}} \right.} \right.\)
Vậy hàm số cần tìm là: \(y = {x^2} - 2x + 3\)
c) Parabol có đỉnh \(I(1;4)\) nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{ - \frac{b}{{2a}} = 1}\\{a + b + 3 = 4}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{b = - 2a}\\{a + b = 1}\end{array}\,\, \Leftrightarrow \,\,} \right.} \right.\left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = 2}\end{array}} \right.\)
Vậy hàm số cần tìm là: \(y = - {x^2} + 2x + 3.\)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Xác định Parabol (P): y = ax 2 + b x − 5 biết rằng Parabol đi qua điểm A (3; -4)và có trục đối xứng x = - 3 2
A. y = 1 18 x 2 + 1 6 x − 5
B. y = 1 18 x 2 + 1 6 x + 5
C. y = 3 x 2 + 9 x − 9
D. y = − 1 18 x 2 + 1 6 x − 5
Xem chi tiết Lớp 10 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  7 tháng 3 2017 lúc 18:00
7 tháng 3 2017 lúc 18:00 Đáp án A

 Gửi Hủy
Gửi Hủy 
- Trần Như Đức Thiên
Xác định parabol y = 3x^2+bx+c, biết rằng parabol đó đi qua A(2;19) và nhận đường thẳng x = -2/3 làm trục đối xứng.
Xem chi tiết Lớp 10 Toán 2 0 Gửi Hủy
Gửi Hủy  Akai Haruma Giáo viên 5 tháng 1 2022 lúc 21:10
Akai Haruma Giáo viên 5 tháng 1 2022 lúc 21:10 Lời giải:Parabol đi qua $A(2;19)$ nên $y_A=3x_A^2+bx_A+c$ hay $19=12+2b+c$
$\Rightarrow 2b+c=7(1)$
$x=\frac{-2}{3}$ là trục đối xứng
$\Leftrightarrow \frac{-b}{2.3}=\frac{-2}{3}$
$\Rightarrow b=4(2)$
Từ $(1); (2)\Rightarrow c=-1$
Vậy parabol có pt $y=3x^2+4x-1$
Đúng 3 Bình luận (0) Gửi Hủy
Gửi Hủy  Nguyễn Lê Phước Thịnh CTV
Nguyễn Lê Phước Thịnh CTV  5 tháng 1 2022 lúc 21:07
5 tháng 1 2022 lúc 21:07 Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{-b}{6}=\dfrac{-2}{3}\\12+2b+c=19\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\c=-1\end{matrix}\right.\)
Đúng 1 Bình luận (0) Gửi Hủy
Gửi Hủy 
- MRBEAST??
cho (P): y =2x +bx +c. Tìm các số b,c để đồ thị là một parabol thỏa:a) Đỉnh A(-1;-2)b) Đi qua hai điểm M(0;-1) và N(4;0).c) Đi qua M(1;-2) và có hoành độ đỉnh là 2.đ) Đi qua A(0;4) và có trục đối xứng là đường thẳng x = 1.
Xem chi tiết Lớp 10 Toán Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI 1 0 Gửi Hủy
Gửi Hủy  Nguyễn Lê Phước Thịnh CTV
Nguyễn Lê Phước Thịnh CTV  16 tháng 11 2023 lúc 19:16
16 tháng 11 2023 lúc 19:16 


 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Xác định parabol (P) ; y= ax2+bx+ c biết: c là số nguyên tố chẵn và (P) đi qua B( 3; -4) và có trục đối xứng là x = - 3 2
A. ![]()
B. ![]()
C. ![]()
D. ![]()
 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  3 tháng 1 2018 lúc 3:38
3 tháng 1 2018 lúc 3:38 Ta có c là số nguyên tố chẵn nên c= 2
Do (P) đi qua B(3; -4) nên -4=9a+3b+2 (1)
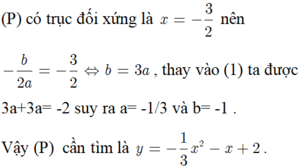
Chọn A.
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Nguyễn Mỹ Linh
xác định parabol y= a^2+bx+2 biết rằng p đi qua điểm m (1;5) và có trục đối xứng là đường thẳng x= -1/4
Xem chi tiết Lớp 10 Toán §3. Hàm số bậc hai 1 0 Gửi Hủy
Gửi Hủy  Phía sau một cô gái
Phía sau một cô gái  6 tháng 3 2023 lúc 20:21
6 tháng 3 2023 lúc 20:21 \(\left(P\right):y=ax^2+bx+2\)
Vì (P) đi qua điểm \(M\left(1;5\right)\) nên ta có: \(a.1^2+b.1+2=5\Leftrightarrow a+b=3\) (1)
Mà (P) có trục đối xứng là \(x=\dfrac{-1}{4}\) nên: \(\dfrac{-b}{2a}=\dfrac{-1}{4}\)
\(\Leftrightarrow-2a=-4b\Leftrightarrow-2a+4b=0\) (2)
Từ (1) và (2) ta có:
\(\left\{{}\begin{matrix}a+b=3\\-2a+4b=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
Vậy parabol cần tìm có dạng: \(y=2x^2=x+2\)
Đúng 4 Bình luận (2)
 Gửi Hủy
Gửi Hủy Khoá học trên OLM (olm.vn)
- Toán lớp 10 (Kết nối tri thức với cuộc sống)
- Toán lớp 10 (Cánh Diều)
- Toán lớp 10 (Chân trời sáng tạo)
- Ngữ văn lớp 10 (Kết nối tri thức với cuộc sống)
- Ngữ văn lớp 10 (Cánh Diều)
- Ngữ văn lớp 10 (Chân trời sáng tạo)
- Tiếng Anh lớp 10 (i-Learn Smart World)
- Tiếng Anh lớp 10 (Global Success)
- Vật lý lớp 10 (Kết nối tri thức với cuộc sống)
- Vật lý lớp 10 (Cánh diều)
- Hoá học lớp 10 (Kết nối tri thức với cuộc sống)
- Hoá học lớp 10 (Cánh diều)
- Sinh học lớp 10 (Kết nối tri thức với cuộc sống)
- Sinh học lớp 10 (Cánh diều)
- Lịch sử lớp 10 (Kết nối tri thức với cuộc sống)
- Lịch sử lớp 10 (Cánh diều)
- Địa lý lớp 10 (Kết nối tri thức với cuộc sống)
- Địa lý lớp 10 (Cánh diều)
- Giáo dục kinh tế và pháp luật lớp 10 (Kết nối tri thức với cuộc sống)
- Giáo dục kinh tế và pháp luật lớp 10 (Cánh diều)
- Lập trình Python cơ bản
Từ khóa » Trục đối Xứng Y=ax^2+bx+c
-
Xác định Parabol Y=ax^2+bx+c Có Trục đối X=5/6 - Nguyễn Lê Tín
-
Xác định Parabol (P): Y=x^2+bx+c Có Trục đối Xứng Là X
-
Cách Tìm Trục đối Xứng Của Hàm Số Bậc Hai - Tin Tức 2022
-
Tìm A,b,c Của Parabol Ax2 Bx C = Y Có Trục đối Xứng X = 1,và điểm A(2;3)
-
4) Và Nhận đường Thẳng X = 1 Làm Trục đối Xứng - Toán Học Lớp 10
-
Xác định Parabol (P) Biết (P): Y = Ax^2 + Bx + 2 đi Qua điểm A (1
-
Y=ax^2+bx+5 Biết (P) đi Qua A (3; -4) Và Có Trục đối Xứng X
-
Xác định Tọa độ đỉnh, Phương Trình Của Trục đối Xứng Của Parabol...
-
Parabol Y=ax2+bx+c đi Qua M(2;−7) Và N(−5;0) Và Có Trục đối Xứng X
-
Xác định Tọa độ đỉnh, Phương Trình Của Trục đối Xứng Của Parabol Y ...
-
Phương Trình Parabol (P) : Y = Ax^2 + Bx + 2 đi Qua điểm M( 1
-
Biết Parabol Nhận Trục Tung Làm Trục đối Xứng Và Cắt đường Thẳng Y=x2
-
Vẽ Thành Thạo Các Parabol Y Ax = 2+ +bx C Bằng Cách Xác định đỉnh ...
-
Tìm A,b để đồ Thị Hàm Số Y=ax2+bx+2 đi Qua điểm A(3,5) Và Có ...
