Xét Tính đơn điệu (đồng Biến, Nghịch Biến) Của Hàm Số

Xét tính đơn điệu (đồng biến, nghịch biến) của hàm số Chuyên đề môn Toán lớp 10 Bài trước Bài sau Lớp: Lớp 10 Môn: Toán Dạng tài liệu: Chuyên đề Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Chuyên đề Toán học lớp 10: Xét tính đơn điệu (đồng biến, nghịch biến) của hàm số được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.

Chuyên đề: Xét tính đơn điệu (đồng biến, nghịch biến) của hàm số

• 1. Phương pháp giải.
• 2. Các ví dụ minh họa.

1. Phương pháp giải.

C1: Cho hàm số y = f(x) xác định trên K. Lấy x1; x2 ∈ K;x1 < x2, đặt T = f(x1 )-f(x2 )

+ Hàm số đồng biến trên K ⇔ T > 0.

+ Hàm số nghịch biến trên K ⇔ T < 0.

C2: Cho hàm số y = f(x) xác định trên K. Lấy x1; x2 ∈ K;x1 ≠ x2, đặt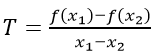

+ Hàm số đồng biến trên K ⇔ T > 0.

+ Hàm số nghịch biến trên K ⇔ T < 0.

2. Các ví dụ minh họa.

Ví dụ 1: Xét sự biến thiên của hàm số sau trên khoảng (1; + ∞)

a) y = 3/(x-1)

b) y = x + 1/x

Hướng dẫn:

a) Với mọi x1; x2 ∈ (1; + ∞); x1 ≠ x2 ta có:

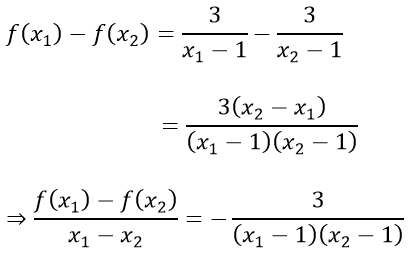
Vì x1 > 1; x2 > 1 nên

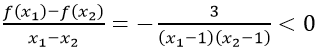
Do đó hàm số y = 3/(x-1) nghịch biến trên khoảng (1; + ∞).

b) Với mọi x1; x2 ∈ (1; + ∞); x1 ≠ x2 ta có:

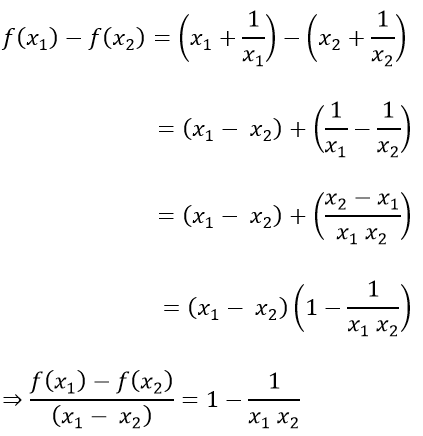
Vì x1 > 1; x2 > 1

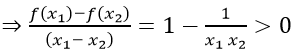nên hàm số y = x + 1/x đồng biến trên khoảng (1; + ∞).

Ví dụ 2: Cho hàm số y = f(x) = x2 - 4

a) Xét chiều biến thiên cuả hàm số trên (- ∞;0) và trên (0;+ ∞)

b) Lập bảng biến thiên của hàm số trên [-1;3] từ đó xác định giá trị lớn nhất, nhỏ nhất của hàm số trên[-1;3].

Hướng dẫn:

TXĐ: D = R.

a) ∀ x1; x2 ∈ R; x1 < x2 ⇒ x2 - x1 > 0

Ta có T = f(x2 ) - f(x1 )=(x22 - 4) - (x12 - 4) = (x2 - x1 )(x2 + x1 )

Nếu x1; x2 ∈ (- ∞;0) thì T < 0. Vậy hàm số y=f(x) nghịch biến trên (- ∞;0).

Nếu x1; x2 ∈ (0; + ∞) thì T > 0. Vậy hàm số y = f(x) đồng biến trên (0; + ∞).

b) Bảng biến thiên của hàm số y = f(x) = x2 - 4 trên [-1; 3]

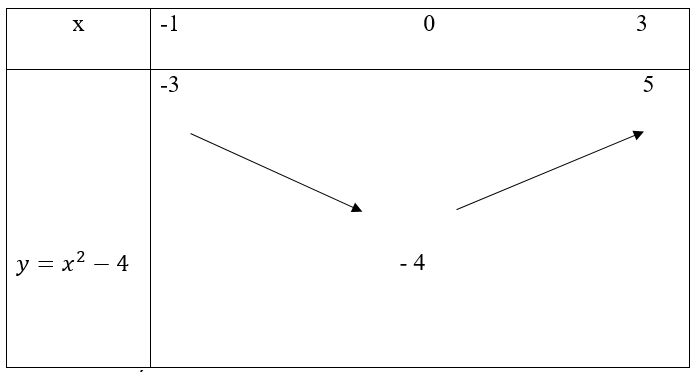
Dựa vào bảng biến thiên ta có:

Giá trị lớn nhất của hàm số trên [-1; 3] là 5, đạt được khi x = 3.

Giá trị nhỏ nhất của hàm số trên [-1; 3] là – 4, đạt được khi x = 0.

Ví dụ 3: Xét sự biến thiên của hàm sốtrên tập xác định của nó.

Áp dụng tìm số nghiệm của các phương trình sau:

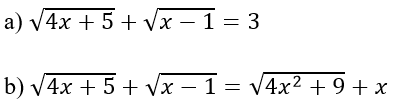
Hướng dẫn:

ĐKXĐ: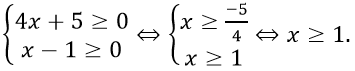

Suy ra TXĐ: D = [1; + ∞)

Với mọi x1; x2 ∈ [1; + ∞), x1 ≠ x2, ta có:

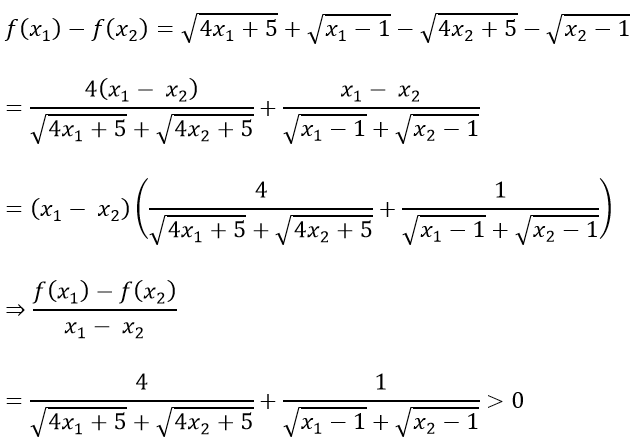
Nên hàm sốđồng biến trên khoảng [1; + ∞).

a) Vì hàm số đã cho đồng biến trên [1; + ∞) nên

Nếu x > 1 ⇒ f(x) > f(1) hay

Suy ra phương trìnhkhông có nghiệm x > 1.

Với x = 1 dễ thấy nó là nghiệm của phương trình đã cho

Vậy phương trình có nghiệm duy nhất x = 1.

b)

ĐKXĐ: x ≥ 1

Đặt x2 + 1 = t, t ≥ 1 ⇒ x2 = t - 1

Do x ≥ 1 nên x = √(t-1). Khi đó phương trình trở thành:

⇔ f(x)=f(t)

Nếu x > t ⇒ f(x) > f(t) hay

Suy ra phương trình đã cho không có nghiệm thỏa mãn x > t.

Nếu x < t ⇒ f(x)< f(t) hay

Suy ra phương trình đã cho không có nghiệm thỏa mãn x < t.

Vậy f(x) = f(t) ⇔ x = t hay x2 + 1 = x ⇔ x2 - x + 1 = 0 (vô nghiệm)

Vậy phương trình đã cho vô nghiệm.

Nhận xét:

Hàm số y = f(x) đồng biến (hoặc nghịch biến) trên toàn bộ tập xác định thì phương trình f(x)=0 có tối đa một nghiệm.

Nếu hàm số y = f(x) đồng biến (nghịch biến) trên D thì f(x) > f(y) ⇔ x > y (x < y) và f(x) = f(y) ⇔ x = y ∀ x,y ∈ D. Tính chất này được sử dụng nhiều trong các bài toán đại số như giải phương trình , bất phương trình , hệ phương trình và các bài toán cực trị.

Với nội dung bài Xét tính đơn điệu (đồng biến, nghịch biến) của hàm số trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững phương pháp giải, cách tính đồng biến hay nghịch biến của một hàm số....

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Xét tính đơn điệu (đồng biến, nghịch biến) của hàm số. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc