4.2: Graphs Of Exponential Functions - Mathematics LibreTexts

Example \(\PageIndex{5}\)

Sketch the graphs of \( g(x) = -2 \cdot 3^{x-5}+6 \) and \( f(x) = 3 \cdot 2^{-x+1}-4 \) and the corresponding original parent function. State the domain, range, and horizontal asymptote of the transformation.

Solution

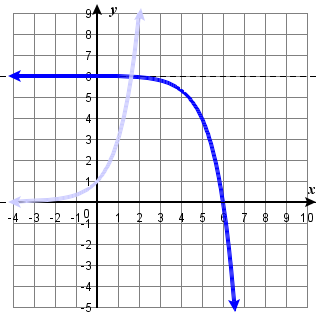The basic parent function for \( g(x) = -2 \cdot 3^{x-5}+6 \) is \( y = 3^x\).

The transformations needed to obtain the graph of \(g(x)\) from the graph of \(y\) are:

1. Shift right 5 units ( \( x \rightarrow x+5 \) )
2. Reflect over the \(x\)-axis ( \( y \rightarrow -y \) )
3. Vertically stretch by a factor of 2 ( \( y \rightarrow 2y \) )
4. Shift up \(6\) units ( \( y \rightarrow y-4 \) )

The graph of \(g(x)\) and its parent function is on the right.

The domain is \((−\infty,\infty)\); the range is \((-\infty, 6)\); the horizontal asymptote is \(y=6\).

If tables are used to graph the function, coordinate points for the parent function appear in the table below

\( \begin{array}{|r|c|c|c|c| c |} \hline \text{Parent function: }x & \text{HA} & -1 & 0 & 1 & 2 \\ \hline y = 3^x & 0 & \frac{1}{3} & 1 & 3 & 9 \\[2pt] \hline \end{array} \)

Corresponding coordinate points for the transformation \( g(x) = -2 \cdot 3^{x-5}+6 \) would be

\( \begin{array}{|r|c|c|c|c| c |} \hline \text{New }x \text{ is: } \:\;\quad x+5 & \text{HA} & 4 & 5 & 6 & 7 \\ \hline \text{New } y \text{ is: } -2y+6 & 6 & 5\frac{1}{3} & 4 & 0 & -12 \\[2pt] \hline \end{array} \)

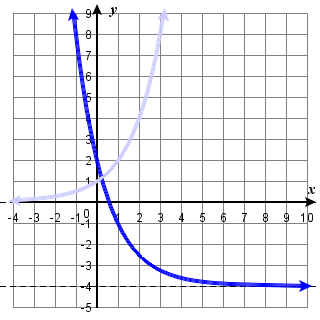The basic parent function for \( f(x) = 3 \cdot 2^{-x+1}-4 \) is \( y = 2^x\).

The transformations needed to obtain the graph of \(f(x)\) from the graph of \(y\) are:

1. Shift left 1 unit ( \( x \rightarrow x-1 \) )
2. Reflect over the \(y\)-axis ( \( x \rightarrow -x \) )
3. Vertically stretch by a factor of 3 ( \( y \rightarrow 3y \) )
4. Shift down \(4\) units ( \( y \rightarrow y-4 \) )

If instead we re-wrote the function in the form: \( f(x) = 3 \cdot 2^{-(x-1)}-4 \), the transformations would be

1. Reflect over the \(y\)-axis ( \( x \rightarrow -x \) )
2. Shift right 1 unit ( \( x \rightarrow x+1 \) )
3. Vertically stretch by a factor of 3 ( \( y \rightarrow 3y \) )
4. Shift down \(4\) units ( \( y \rightarrow y-4 \) )

The graph of \(f(x)\) and its parent function is on the right.

The domain is \((−\infty,\infty)\); the range is \((\infty, -4)\); the horizontal asymptote is \(y=-4\).

If tables are used to graph the function, coordinate points for the parent function appear in the table below

\( \begin{array}{|r|c|c|c|c| c |} \hline \text{Parent function: }x & \text{HA} & -1 & 0 & 1 & 2 \\ \hline y = 2^x & 0 & \frac{1}{2} & 1 & 2 & 4 \\[2pt] \hline \end{array} \)

Corresponding coordinate points for the transformation \( f(x) = 3 \cdot 2^{-x+1}-4 \) would be

\( \begin{array}{|r|c|c|c|c| c |} \hline \text{New } x \text{ is: } -x+1 & \text{HA} & 2 & 1 & 0 & -1 \\ \hline \text{New } y \text{ is: } 3y-4 & -4 & -2\frac{1}{2} & -1 & 2 & 8 \\[2pt] \hline \end{array} \)