5.3: Graphs Of Exponential Functions - Mathematics LibreTexts

Graphing Exponential Functions

Before we begin graphing, it is helpful to review the behavior of exponential growth. Recall the table of values for a function of the form \(f(x)=b^x\) whose base is greater than one. We’ll use the function \(f(x)=2^x\). Observe how the output values in Table \(\PageIndex{1}\) change as the input increases by \(1\).

Table \(\PageIndex{1}\)

\(x\)	\(−3\)	\(−2\)	\(−1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(f(x)=2^x\)	\(\dfrac{1}{8}\)	\(\dfrac{1}{4}\)	\(\dfrac{1}{2}\)	\(1\)	\(2\)	\(4\)	\(8\)

Each output value is the product of the previous output and the base, \(2\). We call the base \(2\) the growth factor. In fact, for any exponential function with the form \(f(x)=ab^x\), \(b\) is the growth factor of the function. This means that as the input increases by \(1\), the output value will be the product of the base and the previous output, regardless of the value of \(a\).

Notice from the table that

• the output values are positive for all values of \(x\);
• as \(x\) increases, the output values increase without bound; and
• as \(x\) decreases, the output values grow smaller, approaching zero.

Figure \(\PageIndex{1}\) shows the exponential growth function \(f(x)=2^x\).

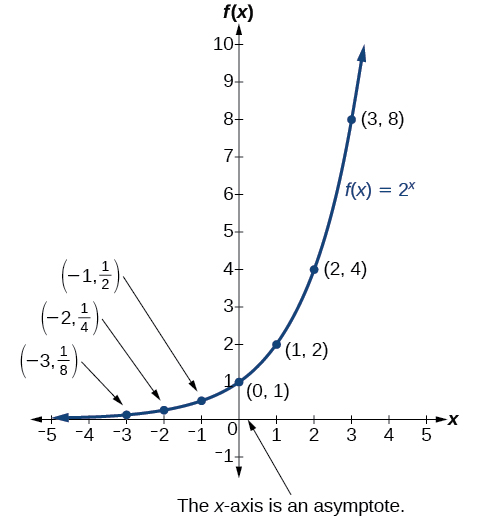
Figure \(\PageIndex{1}\): Notice that the graph gets close to the \(x\)-axis, but never touches it.

The domain of \(f(x)=2^x\) is all real numbers, the range is \((0,\infty)\), and the horizontal asymptote is \(y=0\). Note that, unlike a horizontal asymptote for a rational function (see Section 4.8), the graph approaches \(y=0\) only at one end.

To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form \(f(x)=b^x\) whose base is between zero and one. We’ll use the function \(g(x)={\left(\dfrac{1}{2}\right)}^x\). Observe how the output values in Table \(\PageIndex{2}\) change as the input increases by \(1\).

Table \(\PageIndex{2}\)

\(x\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(g(x)={\left(\dfrac{1}{2}\right)}^x\)	\(8\)	\(4\)	\(2\)	\(1\)	\(\dfrac{1}{2}\)	\(\dfrac{1}{4}\)	\(\dfrac{1}{8}\)

Again, because the input is increasing by \(1\), each output value is the product of the previous output and the base, or growth factor \(\dfrac{1}{2}\). Since we are multiplying by a factor that is less than 1, we have "negative growth," or decay.

Notice from the table that

• the output values are positive for all values of \(x\);
• as \(x\) increases, the output values grow smaller, approaching zero; and
• as \(x\) decreases, the output values grow without bound.

Figure \(\PageIndex{2}\) shows the exponential decay function, \(g(x)={\left(\dfrac{1}{2}\right)}^x\).

Figure \(\PageIndex{2}\)

The domain of \(g(x)=\left(\frac{1}{2}\right)^x\) is all real numbers, the range is \((0,\infty)\), and the horizontal asymptote is \(y=0\).

CHARACTERISTICS OF THE GRAPH OF THE TOOLKIT FUNCTION \(f(x) = b^x\)

An exponential function with the form \(f(x)=b^x\), \(b>0\), \(b≠1\), has these characteristics:

• one-to-one function
• horizontal asymptote: \(y=0\)
• domain: \((–\infty, \infty)\)
• range: \((0,\infty)\)
• \(x\)-intercept: none
• \(y\)-intercept: \((0,1)\) 
• increasing if \(b>1\)
• decreasing if \(b<1\)

Figure \(\PageIndex{3}\) compares the graphs of exponential growth and decay functions.

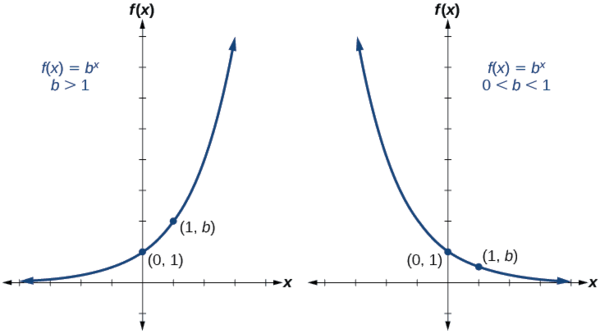
Figure \(\PageIndex{3}\)

Given an exponential function of the form \(f(x)=b^x\), graph the function

1. Plot at least \(3\) points of the graph by finding 3 input-output pairs, including the \(y\)-intercept \((0,1)\).
2. Draw a smooth curve through the points.
3. State the domain, \((−\infty,\infty)\), the range, \((0,\infty)\), and the horizontal asymptote,  \(y=0\).

Example \(\PageIndex{1}\): Sketch the Graph of an Exponential Function of the Form \(f(x) = b^x\)

Sketch a graph of \(f(x)=(0.25)^x\). State the domain, range, and asymptote.

Solution

Since \(b=0.25\)  is between zero and one, we know the function is decreasing. The end behavior of the graph is as follows: as \(x \rightarrow -\infty\), \(y \rightarrow \infty\), and as \(x \rightarrow \infty\), \(y \rightarrow 0\), so the graph has an asymptote \(y=0\).

• The \(y\)-intercept is \((0,1)\).
• Find two other points.
• Plot the \(y\)-intercept, along with the two other points. We will use \((−1,4)\) and \((1,0.25)\).

Draw a smooth curve connecting the points as in Figure \(\PageIndex{4}\).

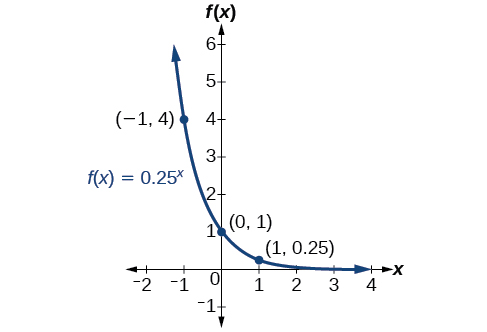
Figure \(\PageIndex{4}\)

The domain is \((−\infty,\infty)\); the range is \((0,\infty)\); the horizontal asymptote is \(y=0\).

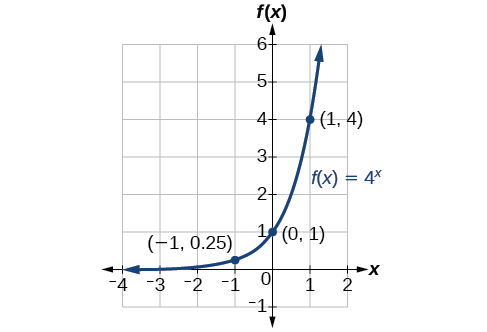
\(\PageIndex{1}\) Sketch the graph of \(f(x)=4^x\). State the domain, range, and asymptote.

Answer

The domain is \((−\infty,\infty)\); the range is \((0,\infty)\); the horizontal asymptote is \(y=0\).