Graphs Of Exponential Functions | College Algebra - Lumen Learning

Learning Outcomes

• Determine whether an exponential function and its associated graph represents growth or decay.
• Sketch a graph of an exponential function.
• Graph exponential functions shifted horizontally or vertically and write the associated equation.
• Graph a stretched or compressed exponential function.
• Graph a reflected exponential function.
• Write the equation of an exponential function that has been transformed.

As we discussed in the previous section, exponential functions are used for many real-world applications such as finance, forensics, computer science, and most of the life sciences. Working with an equation that describes a real-world situation gives us a method for making predictions. Most of the time, however, the equation itself is not enough. We learn a lot about things by seeing their visual representations, and that is exactly why graphing exponential equations is a powerful tool. It gives us another layer of insight for predicting future events.

Characteristics of Graphs of Exponential Functions

Before we begin graphing, it is helpful to review the behavior of exponential growth. Recall the table of values for a function of the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is greater than one. We’ll use the function [latex]f\left(x\right)={2}^{x}[/latex]. Observe how the output values in the table below change as the input increases by 1.

x	–3	–2	–1	0	1	2	3
[latex]f\left(x\right)={2}^{x}[/latex]	[latex]\frac{1}{8}[/latex]	[latex]\frac{1}{4}[/latex]	[latex]\frac{1}{2}[/latex]	1	2	4	8

Each output value is the product of the previous output and the base, 2. We call the base 2 the constant ratio. In fact, for any exponential function with the form [latex]f\left(x\right)=a{b}^{x}[/latex], b is the constant ratio of the function. This means that as the input increases by 1, the output value will be the product of the base and the previous output, regardless of the value of a.

Notice from the table that:

• the output values are positive for all values of x
• as x increases, the output values increase without bound
• as x decreases, the output values grow smaller, approaching zero

The graph below shows the exponential growth function [latex]f\left(x\right)={2}^{x}[/latex].

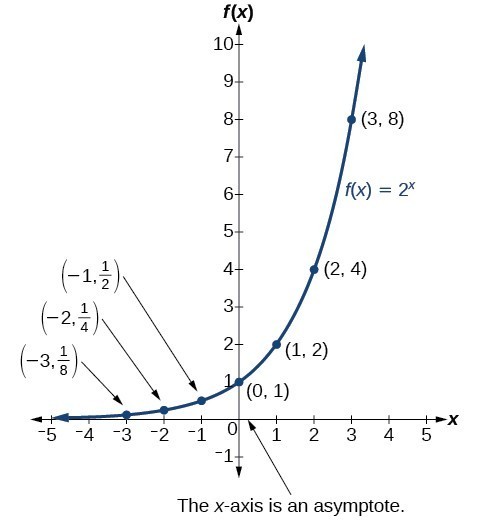
Notice that the graph gets close to the x-axis but never touches it.

The domain of [latex]f\left(x\right)={2}^{x}[/latex] is all real numbers, the range is [latex]\left(0,\infty \right)[/latex], and the horizontal asymptote is [latex]y=0[/latex].

To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is between zero and one. We’ll use the function [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex]. Observe how the output values in the table below change as the input increases by 1.

x	–3	–2	–1	0	1	2	3
[latex]g\left(x\right)=\left(\frac{1}{2}\right)^{x}[/latex]	8	4	2	1	[latex]\frac{1}{2}[/latex]	[latex]\frac{1}{4}[/latex]	[latex]\frac{1}{8}[/latex]

Again, because the input is increasing by 1, each output value is the product of the previous output and the base or constant ratio [latex]\frac{1}{2}[/latex].

Notice from the table that:

• the output values are positive for all values of x
• as x increases, the output values grow smaller, approaching zero
• as x decreases, the output values grow without bound

The graph below shows the exponential decay function, [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex].

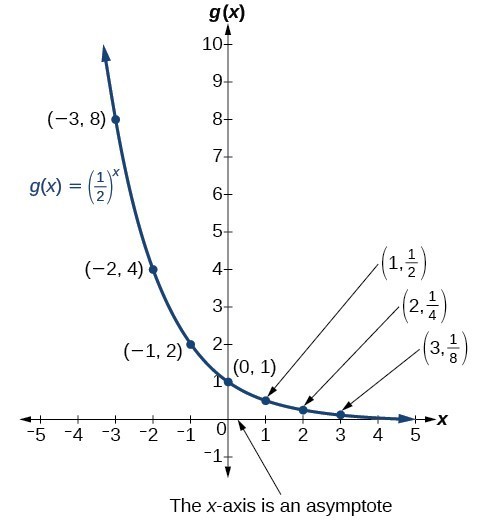
The domain of [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex] is all real numbers, the range is [latex]\left(0,\infty \right)[/latex], and the horizontal asymptote is [latex]y=0[/latex].

A General Note: Characteristics of the Graph of the Parent Function [latex]f\left(x\right)={b}^{x}[/latex]

An exponential function with the form [latex]f\left(x\right)={b}^{x}[/latex], [latex]b>0[/latex], [latex]b\ne 1[/latex], has these characteristics:

• one-to-one function
• horizontal asymptote: [latex]y=0[/latex]
• domain: [latex]\left(-\infty , \infty \right)[/latex]
• range: [latex]\left(0,\infty \right)[/latex]
• x-intercept: none
• y-intercept: [latex]\left(0,1\right)[/latex]
• increasing if [latex]b>1[/latex]
• decreasing if [latex]b0[/latex]. For example, if we begin by graphing the parent function [latex]f\left(x\right)={2}^{x}[/latex], we can then graph the stretch, using [latex]a=3[/latex], to get [latex]g\left(x\right)=3{\left(2\right)}^{x}[/latex] and the compression, using [latex]a=\frac{1}{3}[/latex], to get [latex]h\left(x\right)=\frac{1}{3}{\left(2\right)}^{x}[/latex].
  

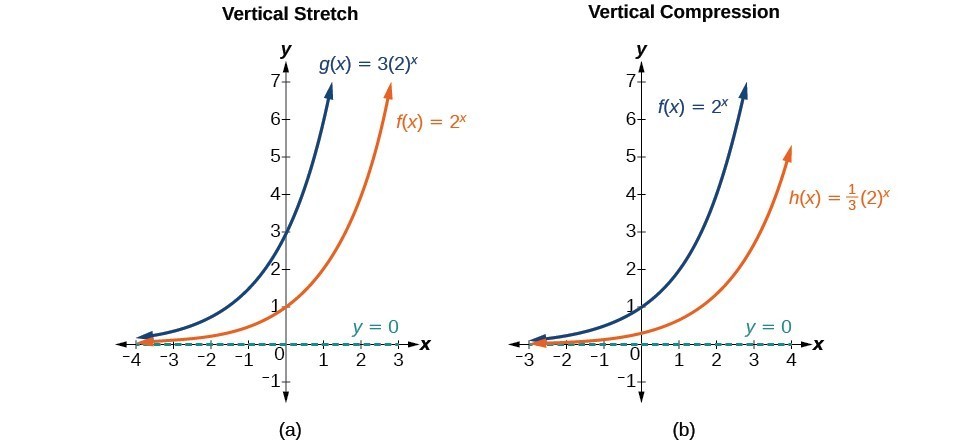
  (a) [latex]g\left(x\right)=3{\left(2\right)}^{x}[/latex] stretches the graph of [latex]f\left(x\right)={2}^{x}[/latex] vertically by a factor of 3. (b) [latex]h\left(x\right)=\frac{1}{3}{\left(2\right)}^{x}[/latex] compresses the graph of [latex]f\left(x\right)={2}^{x}[/latex] vertically by a factor of [latex]\frac{1}{3}[/latex].

  A General Note: Stretches and Compressions of the Parent Function [latex]f\left(x\right)={b}^{x}[/latex]

  The function [latex]f\left(x\right)=a{b}^{x}[/latex]

  • is stretched vertically by a factor of a if [latex]|a|>1[/latex].
  • is compressed vertically by a factor of a if [latex]|a|1[/latex], is
    • shifted horizontally c units to the left.
    • stretched vertically by a factor of [latex]|a|[/latex] if [latex]|a| > 1[/latex].
    • compressed vertically by a factor of [latex]|a|[/latex] if [latex]0 < |a| < 1[/latex].
    • shifted vertically d units.
    • reflected about the x-axis when a < 0.

    Note the order of the shifts, transformations, and reflections follow the order of operations.

    Example: Writing a Function from a Description

    Write the equation for the function described below. Give the horizontal asymptote, domain, and range.

    • [latex]f\left(x\right)={e}^{x}[/latex] is vertically stretched by a factor of 2, reflected across the y-axis, and then shifted up 4 units.
    Show Solution

    We want to find an equation of the general form [latex]f\left(x\right)=a{b}^{x+c}+d[/latex]. We use the description provided to find a, b, c, and d.

    • We are given the parent function [latex]f\left(x\right)={e}^{x}[/latex], so b = e.
    • The function is stretched by a factor of 2, so a = 2.
    • The function is reflected about the y-axis. We replace x with –x to get: [latex]{e}^{-x}[/latex].
    • The graph is shifted vertically 4 units, so d = 4.

    Substituting in the general form, we get:

    [latex]\begin{array}{llll}f\left(x\right)\hfill & =a{b}^{x+c}+d\hfill \\ \hfill & =2{e}^{-x+0}+4\hfill \\ \hfill & =2{e}^{-x}+4\hfill \end{array}[/latex]

    The domain is [latex]\left(-\infty ,\infty \right)[/latex]; the range is [latex]\left(4,\infty \right)[/latex]; the horizontal asymptote is [latex]y=4[/latex].

    Try It

    Write the equation for the function described below. Give the horizontal asymptote, the domain, and the range.

    • [latex]f\left(x\right)={e}^{x}[/latex] is compressed vertically by a factor of [latex]\frac{1}{3}[/latex], reflected across the x-axis, and then shifted down 2 units.
    Show Solution

    [latex]f\left(x\right)=-\frac{1}{3}{e}^{x}-2[/latex]; the domain is [latex]\left(-\infty ,\infty \right)[/latex]; the range is [latex]\left(-\infty ,2\right)[/latex]; the horizontal asymptote is [latex]y=2[/latex].

    Using a Graph to Approximate a Solution to an Exponential Equation

    Graphing can help you confirm or find the solution to an exponential equation. For example,[latex]42=1.2{\left(5\right)}^{x}+2.8[/latex] can be solved to find the specific value for x that makes it a true statement. Graphing [latex]y=4[/latex] along with [latex]y=2^{x}[/latex] in the same window, the point(s) of intersection if any represent the solutions of the equation.

    To use a calculator to solve this, press [Y=] and enter [latex]1.2(5)x+2.8[/latex] next to Y1=. Then enter 42 next to Y2=. For a window, use the values –3 to 3 for[latex]x[/latex] and –5 to 55 for[latex]y[/latex].Press [GRAPH]. The graphs should intersect somewhere near[latex]x=2[/latex].

    For a better approximation, press [2ND] then [CALC]. Select [5: intersect] and press [ENTER] three times. The x-coordinate of the point of intersection is displayed as 2.1661943. (Your answer may be different if you use a different window or use a different value for Guess?) To the nearest thousandth,x≈2.166.

    Try It

    Solve [latex]4=7.85{\left(1.15\right)}^{x}-2.27[/latex] graphically. Round to the nearest thousandth.

    Show Solution

    [latex]x\approx -1.608[/latex]

    Key Equations

    General Form for the Transformation of the Parent Function [latex]\text{ }f\left(x\right)={b}^{x}[/latex]

    [latex]f\left(x\right)=a{b}^{x+c}+d[/latex]

    Key Concepts

    • The graph of the function [latex]f\left(x\right)={b}^{x}[/latex] has a y-intercept at [latex]\left(0, 1\right)[/latex], domain of [latex]\left(-\infty , \infty \right)[/latex], range of [latex]\left(0, \infty \right)[/latex], and horizontal asymptote of [latex]y=0[/latex].
    • If [latex]b>1[/latex], the function is increasing. The left tail of the graph will approach the asymptote [latex]y=0[/latex], and the right tail will increase without bound.
    • If 0 < b < 1, the function is decreasing. The left tail of the graph will increase without bound, and the right tail will approach the asymptote [latex]y=0[/latex].
    • The equation [latex]f\left(x\right)={b}^{x}+d[/latex] represents a vertical shift of the parent function [latex]f\left(x\right)={b}^{x}[/latex].
    • The equation [latex]f\left(x\right)={b}^{x+c}[/latex] represents a horizontal shift of the parent function [latex]f\left(x\right)={b}^{x}[/latex].
    • The equation [latex]f\left(x\right)=a{b}^{x}[/latex], where [latex]a>0[/latex], represents a vertical stretch if [latex]|a|>1[/latex] or compression if [latex]0