A → = 3 , B → = 5 - , Góc Giữa →a - A → - Và →b - B

× Đăng nhập Facebook Google ×

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 11 Toán

Câu hỏi:

22/07/2024 5,063

Cho a→=3,b→=5, góc giữa a→ và b→ bằng 120o. Chọn khẳng định sai trong các khẳng định sau?

A. a→+b→=19

B. a→-b→=7

C. a→-2b→=139

D. a→+2b→=9

Đáp án chính xác Xem lời giải Xem lý thuyết Câu hỏi trong đề: Trắc nghiệm hình học Hai đường thẳng vuông góc có đáp án Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Câu trả lời này có hữu ích không?

0 0

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho tứ diện ABCD có AB=AC=AD và . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB→ và IJ→?

Xem đáp án » 02/08/2021 20,246

Câu 2:

Cho tứ diện ABCD có AB=CD=a, IJ=a32 (I, J lần lượt là trung điểm của BC và AD). Số đo góc giữa hai đường thẳng AB và CD là

Xem đáp án » 02/08/2021 17,748

Câu 3:

Cho tứ diện ABCD có AB=AC=AD và BAC^=BAD^=600.Hãy xác định góc giữa cặp vectơ AB→ và CD→?

Xem đáp án » 02/08/2021 14,180

Câu 4:

Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos(AB,DM) bằng :

Xem đáp án » 02/08/2021 13,752

Câu 5:

Cho hình lập phương ABCD.A'B'C'D'. Góc giữa AC và DA' là:

Xem đáp án » 02/08/2021 10,593

Câu 6:

Cho hình lập phương ABCD.A1B1C1D1 có cạnh a. Gọi M là trung điểm AD. Giá trị B1M→.BD1→ là:

Xem đáp án » 02/08/2021 7,231

Câu 7:

Cho hình chóp S.ABC có SA=SB=SC và ASB^=BSC^=CSA^.Hãy xác định góc giữa cặp vectơ SC→ và AB→?

Xem đáp án » 02/08/2021 6,868

Câu 8:

Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc (MN,SC)bằng:

Xem đáp án » 02/08/2021 5,069

Câu 9:

Cho hình chóp S.ABC có AB=AC và SAC^=SAB^. Tính số đo của góc giữa hai đường thẳng chéo nhau SA và BC.

Xem đáp án » 02/08/2021 3,821

Câu 10:

Cho tứ diện ABCD có AC=a, BD=3a. Gọi M,N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN.

Xem đáp án » 02/08/2021 2,388

Câu 11:

Cho tứ diện ABCD có AC= 32AD, CD=AD; BAD^= BAC^=  600. Gọi φ là góc giữa AB và CD. Chọn khẳng định đúng?

Xem đáp án » 02/08/2021 2,226

Câu 12:

Trong không gian cho hai hình vuông ABCD và ABC′D′ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O′. Hãy xác định góc giữa cặp vectơ AB→,OO'→?

Xem đáp án » 02/08/2021 2,051

Câu 13:

Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu?

Xem đáp án » 02/08/2021 1,151

Câu 14:

Trong không gian cho hai tam giác đều ABC và ABC′ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AC,CB,BC′ và C′A . Tứ giác MNPQ là hình gì?

Xem đáp án » 02/08/2021 803 Xem thêm các câu hỏi khác »

LÝ THUYẾT

Mục lục nội dung

Xem thêm

I. Tích vô hướng của hai vecto trong không gian.

1. Góc giữa hai vecto trong không gian.

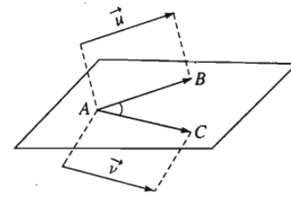
- Định nghĩa. Trong không gian, cho là hai vecto khác vecto- không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao choAB→ = u→ ;  AC→  = v→ . Khi đó, ta gọi góc BAC^  (00  ≤BAC^  ≤1800) là góc giữa hai vecto u→ ;  v→ trong không gian.

Kí hiệu là ( u→ ;  v→).

2. Tích vô hướng của hai vecto trong không gian.

- Định nghĩa:

Trong không gian có hai vecto u→ ;  v→ đều khác vecto- không . Tích vô hướng của hai vecto u→ ;  v→ là một số, kí hiệu là u→ ;  v→, được xác định bởi công thức:

u→ . v→  = u→. v→.cos u→;  v→

Trường hợp u→=  0→ hoặc v→=  0→ ta quy ước: u→ .  v→ = 0.

Ví dụ 1. Cho hình chóp S.ABC có SA= SB= SC và A​SB^  =  BSC^  =  CSA^. Hãy xác định góc giữa cặp vectơ SC→ và AB→?

Lời giải :

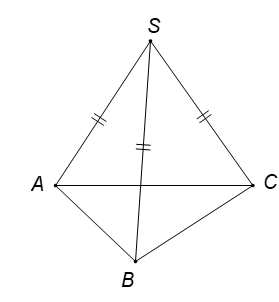
Ta có SC→.AB→=SC→.SB→−SA→=SC→.SB→−SC→.SA→

=SC→.SB→.cosSC→.SB→−SC→.SA→.cosSC→.SA→=SC.SB.cosBSC^−SC.SA.cosASC^

Vì SA= SB= SC và A​SB^  =  BSC^  =  CSA^

⇒SC→.AB→=0

Ta lại có: SC→.SA→=SC→.SA→.cosSC→,SA→

⇒cosSC→,SA→=0

Do đó SC→;  AB→ =900.

II. Vecto chỉ phương của đường thẳng.

1. Định nghĩa.

Nếu a→ khác vecto - không được gọi là vecto chỉ phương của đường thẳng d nếu giá của vecto a→ song song hoặc trùng với đường thẳng d.

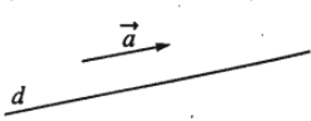
2. Nhận xét.

a) Nếu a→ là vecto chỉ phương của đường thẳng d thì vecto ka→   (k ≠0) cũng là vecto chỉ phương của d.

b) Một đường thẳng d trong không gian hoàn toàn được xác định nếu biết một điểm A thuộc đường thẳng d và một vecto chỉ phương của nó.

c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vecto chỉ phương cùng phương.

III. Góc giữa hai đường thẳng trong không gian.

1. Định nghĩa:

Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.

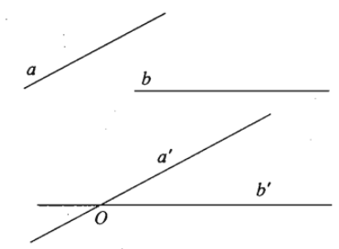
2. Nhận xét.

a) Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.

b) Nếu u→ là vecto chỉ phương của đường thẳng a và v→ là vecto chỉ phương của đường thẳng b và (u→;  v→) =  α thì góc giữa hai đường thẳng a và b bằng α nếu 00≤α≤900 và bằng 1800− α nếu 900< α≤1800 .

Nếu a và b song song hoặc trùng nhau thì góc giữa chúng bằng 0°.

Ví dụ 2. Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa AC và DA’

Lời giải:

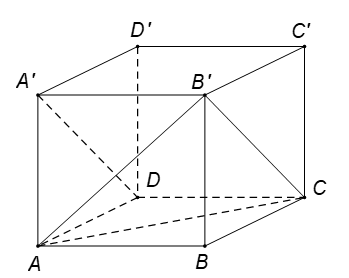
Gọi a là độ dài cạnh hình lập phương.

Khi đó, tam giác AB’C đều (AB’ = B’C= CA = a2)

Do đó B'CA^  =600.

Lại có, DA’ song song CB’ nên

(AC ; DA’) = (AC ; CB’) =B'CA^  =600 .

IV. Hai đường thẳng vuông góc.

1. Định nghĩa.

Hai đường thẳng được gọi là vuông góc nếu góc giữa chúng bằng 90°.

Ta kí hiệu hai đường thẳng a và b vuông góc với nhau là a  ⊥  b.

2. Nhận xét

a) Nếu u→;  v→  lần lượt là các vecto chỉ phương của hai đường thẳng a và b thì a  ⊥  b⇔u→. v→   =0.

b) Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

c) Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.

Ví dụ 3. Cho tứ diện ABCD có AB= AC= AD và BAC^  =  BAD^ =600;  CAD^ =  900. Gọi I và J lần lượt là trung điểm của AB và CD. Chứng minh hai đường thẳng AB và IJ vuông góc với nhau.

Lời giải:

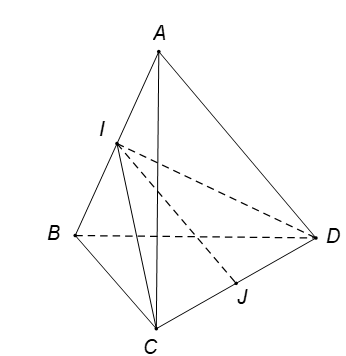
Xét tam giác ICD có J là trung điểm đoạn CD ⇒I​J→=12IC→+ID→.

Tam giác ABC có AB = AC và BAC^ =600nên tam giác ABC đều

⇒CI ⊥AB. (1)

Tương tự, ta có tam giác ABD đều nên DI  ⊥AB. ( 2)

Từ (1) và (2) ta có : IJ→.AB→=12IC→+ID→.AB→=12IC→.AB→+12ID→.AB→=0

⇒IJ→  ⊥AB→ ⇒IJ⊥​AB

Đề thi liên quan

Xem thêm »

• Trắc nghiệm tổng hơp Toán 11 (có đáp án) 76 đề 22949 lượt thi Thi thử
• Trắc nghiệm Đề thi Toán 11 (có đáp án) 17 đề 8267 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án) 12 đề 4836 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 4: Giới hạn (có đáp án) 7 đề 4059 lượt thi Thi thử
• Trắc nghiệm Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (có đáp án) 8 đề 3782 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 5: Đạo hàm (có đáp án) 11 đề 3715 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 2: Tổ hợp - Xác suất (có đáp án) 15 đề 3198 lượt thi Thi thử
• Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác (có đáp án) 6 đề 3132 lượt thi Thi thử
• Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản (có đáp án) 6 đề 3064 lượt thi Thi thử
• Trắc nghiệm Biến cố và xác suất của biến cố có đáp án 4 đề 3042 lượt thi Thi thử

Xem thêm » Hỏi bài

Câu hỏi mới nhất

Xem thêm »

• 

  Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

  \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

  với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

  Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?

  250 18/04/2024 Xem đáp án
• 

  Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

  \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

  với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

  Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?

  138 18/04/2024 Xem đáp án
• 

  Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

  \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

  với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

  Tính chu kì của hàm số h(t)?

  121 18/04/2024 Xem đáp án
• 

  Từ đồ thị hàm số y = sin x, tìm:

  Các khoảng giá trị của x để hàm số y = sin x nhận giá trị dương. 128 18/04/2024 Xem đáp án
• 

  Từ đồ thị hàm số y = sin x, tìm:

  Các giá trị của x để sin x = \(\frac{1}{2}\);

  121 18/04/2024 Xem đáp án
• 

  Từ đồ thị hàm số y = cos x, cho biết:

  Có bao nhiêu giá trị của x trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{3\pi }}{2}} \right)\) để cos x = 0.

  115 18/04/2024 Xem đáp án
• 

  Từ đồ thị hàm số y = cos x, cho biết:

  Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;

  118 18/04/2024 Xem đáp án
• 

  Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

  y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).

  121 18/04/2024 Xem đáp án
• 

  Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

  y = sin x trên khoảng \(\left( { - \frac{{19\pi }}{2};\, - \frac{{17\pi }}{2}} \right),\,\,\left( { - \frac{{13\pi }}{2};\, - \frac{{11\pi }}{2}} \right)\);

  121 18/04/2024 Xem đáp án
• 

  Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:

  \(y = \frac{1}{{4 - \sin x}}\).

  127 18/04/2024 Xem đáp án

Xem thêm »