Bài 3. Ứng Dụng Của Tích Phân Trong Hình Học.

Trang chủ » Giải Toán 12 Trang 121 Bài 5 » Bài 3. Ứng Dụng Của Tích Phân Trong Hình Học.

Có thể bạn quan tâm

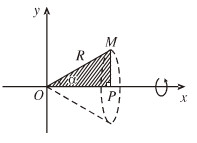
Bài 5. Cho tam giác vuông \(OPM\) có cạnh \(OP\) nằm trên trục \(Ox\). Đặt  \(\widehat {POM} = \alpha \)

và \(OM = R\), \(\left( {0 \le \alpha  \le {\pi  \over 3},R > 0} \right)\)

Gọi 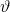  là khối tròn xoay thu được khi quay tam giác đó xung quanh \(Ox\) (H.63).

a) Tính thể tích của 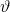 theo \(α\) và \(R\).      

b) Tìm \(α\) sao cho thể tích 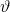 là lớn nhất.  

  

Hướng dẫn giải :

a) Hoành độ điểm \(P\) là : 

Advertisements (Quảng cáo)

\(x_p=  OP = OM. cos α = R.cosα\)

Phương trình đường thẳng \(OM\) là \(y =  tanα.x\). Thể tích \(V\) của khối tròn xoay là:

\(V = \pi \int\limits_0^{R\cos \alpha } {{{\tan }^2}\alpha {{{x^3}} \over 3}\left| {_0^{R\cos \alpha } = {{\pi .{R^3}} \over 3}(\cos \alpha  - {{\cos }^3}} \right.} \alpha )\)

b) Đặt \(t = cosα \Rightarrow t ∈ \left[ {{1 \over 2};1} \right]\). \(\left( \text{ vì }{\alpha  \in \left[ {0;{\pi  \over 3}} \right]} \right)\),  \(α = arccos t\).

Ta có :

\(\eqalign{ & V = {{\pi {R^3}} \over 3}(t - {t^3});V’ = {{\pi {R^3}} \over 3}(1 - 3{t^2}) \cr & V’ = 0 \Leftrightarrow \left[ \matrix{ t = {{\sqrt 3 } \over 3} \hfill \cr t = {{ - \sqrt 3 } \over 3}\text{ (loại)} \hfill \cr} \right. \cr} \)

 Từ đó suy ra \(V\) lớn nhất bằng \({{2\sqrt 3 \pi R^3} \over 27}\) \(\Leftrightarrow t = {{\sqrt 3 } \over 3} \Leftrightarrow \alpha  = \arccos {{\sqrt 3 } \over 3}\)

Từ khóa » Giải Toán 12 Trang 121 Bài 5