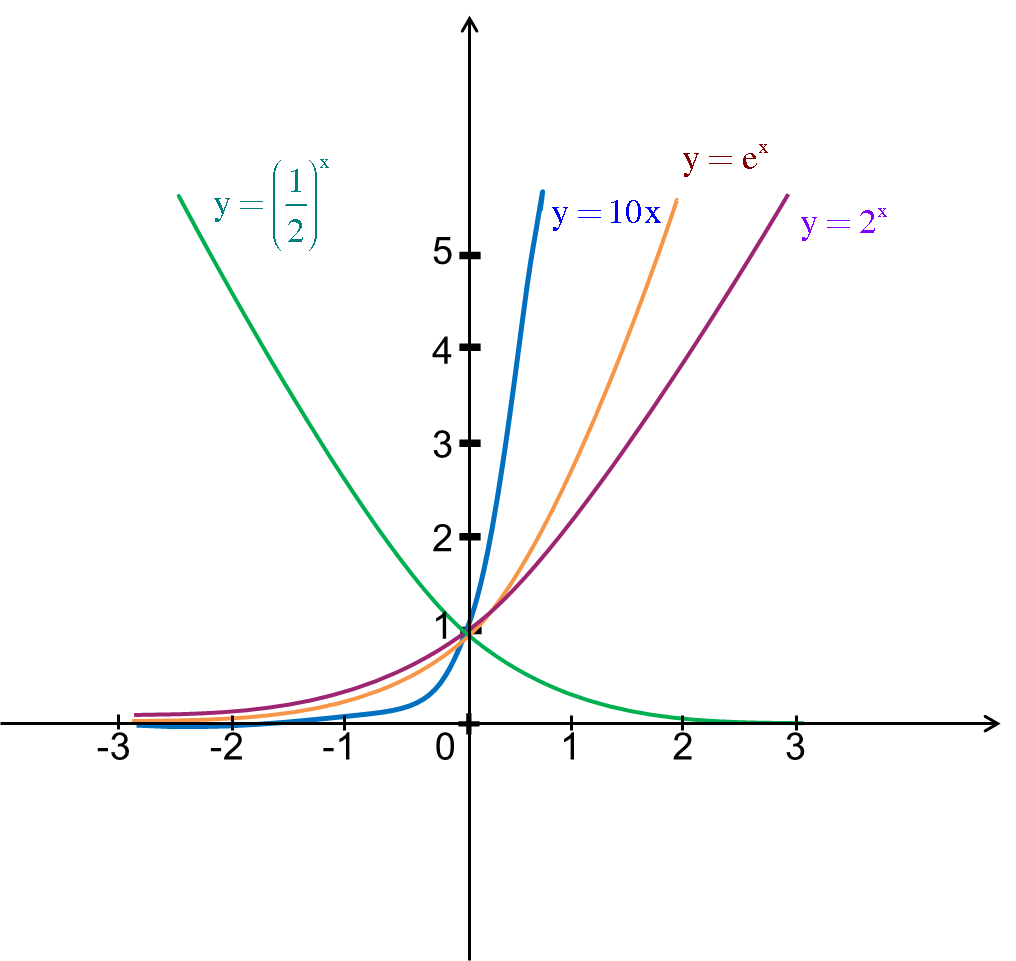
Bài 4. Hàm Số Mũ, Hàm Số Lôgarit - Củng Cố Kiến Thức
Có thể bạn quan tâm
I. Hàm số mũ
Cho số thực dương a khác 1. Hàm số $y = {a^x}$ được gọi là hàm số mũ cơ số a.
* Đạo hàm của hàm số mũ
Định lí 1:
Hàm số $y = {e^x}$ có đạo hàm tại mọi x và $\left( {{e^x}} \right)' = {e^x}$.
Định lí 2:
Hàm số $y = {a^x}\left( {a > 0,a \ne 1} \right)$ có đạo hàm tại mọi x và $\left( {{a^x}} \right)' = {a^x}\ln a$.
* Khảo sát hàm số mũ $y = {a^x}\left( {a > 0,a \ne 1} \right)$
1. $y = {a^x},a > 1$
- Tập xác định: $R$
- Sự biến thiên: $y = {a^x}\ln a > 0,\forall x$
Giới hạn đặc biệt: $\mathop {\lim }\limits_{x \to - \infty } {a^x} = 0,\mathop {\lim }\limits_{x \to + \infty } {a^x} = + \infty $
Tiệm cận:
Trục Ox là tiệm cận ngang.
- Bảng biến thiên: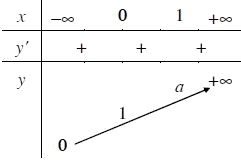
- Đồ thị (Hình 06)
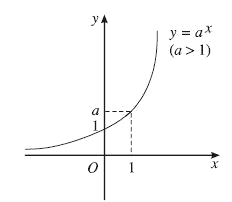
Hình 06
2. $y = {a^x},0 < a < 1$
- Tập xác định: $R$
- Sự biến thiên: $y = {a^x}\ln a < 0,\forall x$
Giới hạn đặc biệt:
$\mathop {\lim }\limits_{x \to - \infty } {a^x} = + \infty ,\mathop {\lim }\limits_{x \to + \infty } {a^x} = 0$
Tiệm cận:
Trục Ox là tiệm cận ngang.
- Bảng biến thiên:

- Đồ thị (Hình 07)
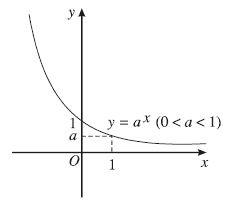
Hình 07
Bảng tóm tắt các tính chất của hàm số mũ $y = {a^x}\left( {a > 0,a \ne 1} \right)$

II. Hàm số lôgarit
Cho số thực dương a khác 1. Hàm số $y = {\log _a}x$ được gọi là hàm số lôgarit cơ số a.
* Đạo hàm của hàm số mũ
Định lí 3:
Hàm số $y = {\log _a}x\left( {a > 0,a \ne 1} \right)$ có đạo hàm tại mọi x>0 và $\left( {{{\log }_a}x} \right)' = \frac{1}{{x\ln a}}$.
Đặc biệt: $\left( {\ln x} \right)' = \frac{1}{x}$
* Khảo sát hàm số mũ $y = {\log _a}x\left( {a > 0,a \ne 1} \right)$
1. $y = {\log _a}x,a > 1$
- Tập xác định: $\left( {0; + \infty } \right)$
- Sự biến thiên: $y' = \frac{1}{{x\ln a}} > 0,\forall x > 0$
Giới hạn đặc biệt: $\mathop {\lim }\limits_{x \to {0^ + }} {\log _a}x = - \infty ,\mathop {\lim }\limits_{x \to + \infty } {\log _a}x = + \infty $
Tiệm cận:
Trục Oy là tiệm cận đứng.
- Bảng biến thiên:

- Đồ thị (Hình 08)
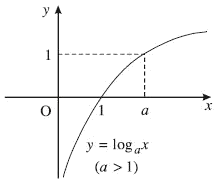
Hình 08
2. $y = {\log _a}x,0 < a < 1$
- Tập xác định: $\left( {0; + \infty } \right)$
- Sự biến thiên: $y' = \frac{1}{{x\ln a}} < 0,\forall x > 0$
Giới hạn đặc biệt: $\mathop {\lim }\limits_{x \to {0^ + }} {\log _a}x = + \infty ,\mathop {\lim }\limits_{x \to + \infty } {\log _a}x = - \infty $
Tiệm cận:
Trục Oy là tiệm cận đứng.
- Bảng biến thiên:
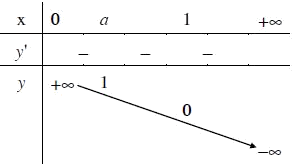
- Đồ thị (Hình 09)
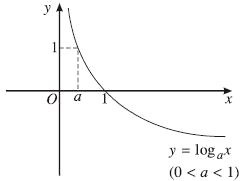
Hình 09
Bảng tóm tắt các tính chất của hàm số $y = {\log _a}x\left( {a > 0,a \ne 1} \right)$
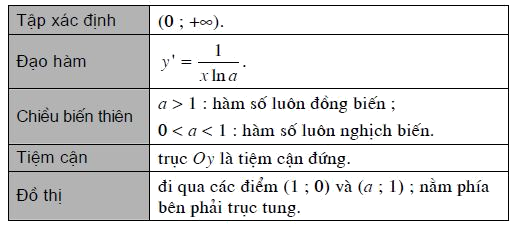
Từ khóa » Hàm Số Logarit Có Tiệm Cận Ngang Không
-
Hàm Số Mũ Và Hàm Số Lôgarit, Trắc Nghiệm Toán Học Lớp 12
-
Bài 4. Hàm Số Mũ Hàm Số Lôgarit
-
Lý Thuyết Hàm Số Mũ, Hàm Số Lôgarit | SGK Toán Lớp 12
-
Tìm Các Đường Tiệm Cận Y=- Logarit Cơ Số 2 Của X+3 | Mathway
-
Tiệm Cận Của đồ Thị Hàm Mũ, Logarit | CPKT THPTQG Môn Toán
-
Hàm Số Mũ Và Hàm Số Logarit: Định Nghĩa, đạo Hàm, Khảo Sát Hàm ...
-
Tiệm Cận đứng Của đồ Thị Hàm Số (y = (log _a)x( (0 < A # 1) ) )
-
Đồ Thị Hàm Số Mũ Và đồ Thị Hàm Số Logarit
-
Đồ Thị Của Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Logarit
-
[PDF] HÀM SỐ LŨY THỪA – HÀM SỐ MŨ – HÀM SỐ LOGARIT | Hoc360.
-
Hàm Số Logarit, Hàm Số Mũ: Lý Thuyết & Bài Tập (Kèm Tài Liệu)
-
Bí Kíp Nhận Dạng đồ Thị Hàm Số Mũ Và Logarit Siêu Nhanh
-
Giải Toán 12: Bài 4. Đường Tiệm Cận Của đồ Thị Hàm Số
-
Bài Giảng Toán 12 - DS_C2_HAM SO LUY THUA-LOGARIT-ml