Bài 4: Hàm Số Mũ Hàm Số Lôgarit - Tìm đáp án, Giải Bài Tập, để Học Tốt
Có thể bạn quan tâm
1. Hàm số mũ
a) Định nghĩa hàm số mũ
Cho số thực dương \(a\) khác 1.
Hàm số \(y=a^x\) được gọi là hàm số mũ cơ số \(a\).
b) Tính chất hàm số mũ
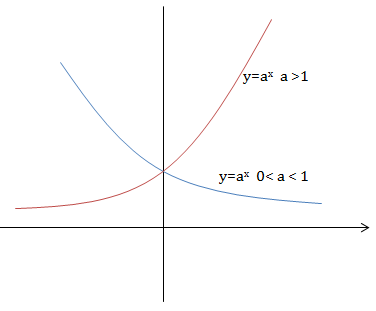
- Tập xác định: \(\mathbb{R}.\)
- Tập giá trị: \((0;+\infty )\)
- Với \(a>1\) hàm số \(y=a^x\) đồng biến trên \(\mathbb{R}.\)
- Với \(0 < a < 1\) hàm số \(y=a^x\) nghịch biến trên \(\mathbb{R}.\)
- Đồ thị hàm số mũ nhận trục \(Ox\) làm tiệm cận ngang.
c) Đạo hàm của hàm số mũ
- Hàm số \(y=e^x\) có đạo hàm với mọi \(x\) và: \(\left ( e^x \right )'=e^x\)
- Hàm số \(y=a^x(a>0,a\ne 1)\) có đạo hàm tại mọi \(x\) và: \(\left( {{a^x}} \right)' = {a^x}{\mathop{\rm lna}\nolimits}\)
- Đối với hàm hợp:
+ \(({e^u})' = u'.{e^u}\)
+ \(({a^u})' = {a^u}.\ln a.u'\)
2. Hàm số Lôgarit
a) Định nghĩa hàm số Lôgarit
Cho số thực dương \(a\) khác 1.
Hàm số \(y=\log_ax\) được gọi là hàm số lôgarit cơ số \(a.\)
b) Tính chất hàm số Lôgarit
- Tập xác định: \(\left( {0; + \infty } \right).\)
- Tập giá trị: \(\mathbb{R}.\)
- Với \(a>1\): \(y=\log_ax\) là hàm số đồng biến trên \(\left( {0; + \infty } \right).\)
- Với \(0 < a < 1\) \(y=\log_ax\) là hàm số nghịch biến trên \(\left( { - \infty ;0} \right)\)
- Với \(x_1>0,x_2>0\): \(\log_ax_1=\log_ax_2\Leftrightarrow x_1=x_2\)
c) Đạo hàm của hàm số logarit
- \(\left( {{{\log }_a}x} \right)' = \frac{1}{{x\ln a}}\)
- \(\left( {{{\log }_a}\left| x \right|} \right)' = \frac{1}{{x\ln a}}\)
- \(\left( {\ln x} \right)' = \frac{1}{x}\)
- Đối với hàm hợp:
+ \(\left( {{{\log }_a}u} \right)' = \frac{{u'}}{{u.\ln a}}\)
+ \(\left( {\ln u} \right)' = \frac{{u'}}{{\ln u}}\)
3. Bài tập minh họa
Ví dụ 1:
Tính đạo hàm các hàm số sau:
a) \(y = \left( {{x^2} - 2x + 2} \right){e^x}\)
b) \(y = {2^{{x^2} - 3x}}\)
c) \(y = \frac{{{2^x} - 1}}{{{5^x}}}\)
d) \(y = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}\)
Lời giải:
a) \(y = \left( {{x^2} - 2x + 2} \right){e^x} \Rightarrow y' = \left( {2x - 2} \right){e^x} + \left( {{x^2} - 2x + 2} \right){e^x} = \left( {{x^2}} \right){e^x}\)
b) \(y = {2^{{x^2} - 3x}} \Rightarrow y' = (2x - 3){.2^{{x^2} - 3x}}.\ln 2\)
c) \(y = \frac{{{2^x} - 1}}{{{5^x}}} = {\left( {\frac{2}{5}} \right)^x} - {\left( {\frac{1}{5}} \right)^x} \Rightarrow y' = {\left( {\frac{2}{5}} \right)^x}.\ln \frac{2}{5} - {\left( {\frac{1}{5}} \right)^x}.\ln \frac{1}{5}\)
d) \(y = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}\)
\(\Rightarrow y' = \frac{{\left( {{e^x} + {e^{ - x}}} \right)\left( {{e^x} + {e^{ - x}}} \right) - \left( {{e^x} - {e^{ - x}}} \right)\left( {{e^x} - {e^{ - x}}} \right)}}{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2}}} = \frac{4}{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2}}}\)
Ví dụ 2:
Tính đạo hàm các hàm số sau:
a) \(y = \ln \left( {{x^2} + 1} \right)\)
b) \(y = \frac{{\ln x}}{x}\)
c) \(y = \left( {1 + \ln x} \right)\ln x\)
d) \(y = {\log _3}(3{x^2} + 2x + 1)\)
Lời giải:
a) \(y = \ln \left( {{x^2} + 1} \right) \Rightarrow y' = \frac{{2x}}{{{x^2} + 1}}\)
b) \(y = \frac{{\ln x}}{x} \Rightarrow y' = \frac{1}{{{x^2}}}\left( {\frac{1}{x}.x - \ln x} \right) = \frac{{1 - \ln x}}{{{x^2}}}\)
c) \(y = \left( {1 + \ln x} \right)\ln x \Rightarrow y' = \frac{{\ln x}}{x} + \frac{{1 + \ln x}}{x} = \frac{{1 + 2\ln x}}{x}\)
d) \(y = {\log _3}(3{x^2} + 2x + 1)\) \(\Rightarrow y' = \frac{{\left( {3{x^2} + 1x + 1} \right)'}}{{(3{x^2} + 2x + 1).\ln 3}} = \frac{{6x + 2}}{{(3{x^2} + 2x + 1).\ln 3}}\)
Ví dụ 3:
Tìm tập xác định của các hàm số sau:
a) \(y = {\log _2}(25 - 4{x^2})\)
b) \(y = {\log _{2x + 1}}(3x + 1) - 2{\log _{3x + 1}}(2x + 1)\)
c) \(y = {\log _{\sqrt {3x + 2} }}(1 - \sqrt {1 - 4{x^2}} )\)
Lời giải:
a) Điều kiện: \(25 - 4{x^2} > 0 \Leftrightarrow - \frac{5}{2} < x < \frac{5}{2}\)
Vậy tập xác định của hàm số là: \(D = \left( { - \frac{5}{2};\frac{5}{2}} \right).\)
b) Điều kiện: \(\left\{ \begin{array}{l} 0 < 2x + 1 \ne 1\\ 0 < 3x + 1 \ne 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - \frac{1}{3}\\ x \ne 0 \end{array} \right.\)
Vậy tập xác định của hàm số là: \(D = \left[ { - \frac{1}{3}; + \infty } \right)\backslash \left\{ 0 \right\}\).
c) Điều kiện: \(\left\{ \begin{array}{l} 0 < 3x + 2 \ne 1\\ 1 - \sqrt {1 - 4{x^2}} > 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x > - \frac{2}{3}\\ x \ne - \frac{1}{3}\\ x \ne 0 \end{array} \right.\)
Vậy tập xác định của hàm số là: \(D = \left( { - \frac{2}{3}; + \infty } \right)\backslash \left\{ { - \frac{1}{3};0} \right\}\).
Ví dụ 4:
Tìm m để hàm số \(y={\log _2}(2{x^2} + 3x + 2m - 1)\) xác định \(\forall x \in \mathbb{R}\).
Lời giải:
Điều kiện: \(2{x^2} + 3x + 2m - 1 > 0,\forall x \in \mathbb{R}\)
Ta có: \(\Delta = {3^2} - 4.2.(2m - 1) = 17 - 16m > 0 \Leftrightarrow m < \frac{{17}}{{16}}.\)
Vậy với \(m<\frac{17}{16}\) hàm số xác định \(\forall x \in \mathbb{R}\).
Từ khóa » Hàm Số Ln
-
Ln (x) - Quy Tắc Logarit Tự Nhiên - RT
-
LN (Hàm LN) - Microsoft Support
-
Bài 4. Hàm Số Mũ, Hàm Số Lôgarit - Củng Cố Kiến Thức
-
[ Mức 1] Tập Xác định Của Hàm Số Y=ln(x−3) Là - Cungthi.online
-
Tập Xác định Của Hàm Số Y = Ln(lnx) Là: | Cungthi.online
-
Tìm M để Hàm Số Y=ln(x^2-2mx+4) Có Tập Xác định D=R - Hoc247
-
Đạo Hàm Ln - Đạo Hàm Hàm Số Mũ
-
Cho Hàm Số F( X ) = Ln X. Tính đạo Hàm Của Hàm Số G( X ) = (log
-
Hàm Số Nào Sau đây Là Một Nguyên Hàm Của Hàm Số Y = Ln X?
-
Cho Hàm Số Y = Ln 7x + 7. Hệ Thức Nào Sau đây Là Hệ Thức đúng?
-
Đạo Hàm Của Hàm Số Y=ln(x^2+2) Là: A...
-
Đạo Hàm Của Hàm Số Y=ln(x^2 +1)/x Tại điểm X=1