Bài Tập Tiệm Cận Của đồ Thị Hàm Số ôn Thi THPT Môn Toán

Trang chủ » Bài Tập Tìm Tiệm Cận đứng Tiệm Cận Ngang » Bài Tập Tiệm Cận Của đồ Thị Hàm Số ôn Thi THPT Môn Toán

Có thể bạn quan tâm

Chuyển đến nội dung Menu

Tài liệu gồm 10 trang, tổng hợp kiến thức cần nhớ, bài tập mẫu, bài tập tương tự và phát triển chủ đề tiệm cận của đồ thị hàm số, có đáp án và lời giải chi tiết, giúp học sinh ôn thi THPT môn Toán.

Các bài toán tiệm cận của đồ thị hàm số được chọn lọc bám sát đề minh họa THPT môn Toán của Bộ Giáo dục và Đào tạo.

1. KIẾN THỨC CẦN NHỚ 1. Đường tiệm cận đứng. Định nghĩa 1. Đường thẳng x = x0 được gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn. 2. Đường tiệm cận ngang. Định nghĩa 2. Đường thẳng y = y0 được gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn. Xét hàm số y = f(x) = P(x)/Q(x) là hàm số phân thức hữu tỷ. – Nếu Q(x) = 0 có nghiệm là x0, và x0 không là nghiệm của P(x) = 0 thì đồ thị có tiệm cận đứng là x = x0. – Nếu bậc P(x) ≤ bậc Q(x) thì đồ thị có tiệm cận ngang. 2. BÀI TẬP MẪU 1. Dạng toán: Đây là dạng tìm tiệm cận của đồ thị hàm số. 2. Hướng giải: Bước 1. Dựa trên giả thiết tính giới hạn của hàm số tại vô cực để tìm tiệm cận ngang. Bước 2. Tính giới hạn dần ra vô cực của hàm số để tìm tiệm cận đứng. 3. BÀI TẬP TƯƠNG TỰ VÀ PHÁT TRIỂN

[ads] TẢI XUỐNG PDF

TÀI LIỆU CÙNG CHUYÊN MỤC

Bài toán VDC đường tiệm cận có chứa tham số Bài tập VDC tiệm cận của đồ thị hàm số có lời giải chi tiết Tài liệu đường tiệm cận của đồ thị hàm số 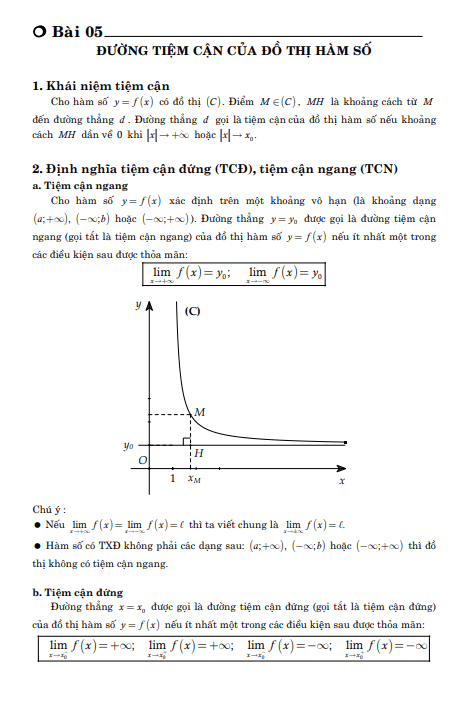55 câu hỏi trắc nghiệm đường tiệm cận của đồ thị hàm số Bài tập toán thực tế sử dụng hàm mũ và lôgarit ôn thi THPT môn Toán Bài tập các phép toán số phức ôn thi THPT môn Toán 111 bài toán vận dụng (8 – 9 – 10) chủ đề toán thực tế Bài toán VDC tìm cực trị của hàm số Đề cương ôn tập HK2 Toán 12 Tài liệu bài toán tối ưu

TÌM KIẾM

Tìm kiếm cho:

GIỚI THIỆU

THI247.com là trang web chia sẻ kiến thức, tài liệu, đề kiểm tra, đề thi học kỳ và đề thi thử các môn thi THPT Quốc gia miễn phí.

BẢN QUYỀN

Các tài liệu trên THI247.com được chúng tôi sưu tầm từ mạng xã hội Facebook và Internet. THI247.com không chịu trách nhiệm về các nội dung có trong tài liệu.

LIÊN HỆ

Địa chỉ: đường Trần Nhân Tông, quận Hai Bà Trưng, thành phố Hà Nội. Email liên hệ: [email protected].

Từ khóa » Bài Tập Tìm Tiệm Cận đứng Tiệm Cận Ngang