Bài Tập Về đường Thẳng Vuông Góc Với Mặt Phẳng - TÀI LIỆU RẺ

Tóm tắt tài liệu

Toggle

• BÀI 2: Cho tứ diện ABCD có 2 mặt ABC và BCD là 2 tam giác cân có chung đáy BC. I là trung điểm của cạnh BC.
• BÀI 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi và có SA = SB =SC = SD
• BÀI 4:Cho tứ diện OABC có 3 cạnh OA, OB, OC đôi một vuông góc.H là chân đường vuông góc hạ từ O tới mp(ABC). C/minh: a) H là trực tâm tam giác ABC.
• Bài 6: Cho hình chóp S.ABCD, có đáy là hình thoi ABCD và có cạnh SA vuông góc với mp(ABCD). Gọi I và K là 2 điểm lấy trên 2 cạnh SB và SD sao cho SI/SB = SD/ SD.
• Bài tập về nhà

Bài tập về đường thẳng vuông góc với mặt phẳng bao gồm một số dạng bài với những phương pháp giải chi tiết, rõ ràng, dễ hiểu. Những bài tập dưới đây mang tính cốt lõi và đặc trưng cho từng dạng, giúp định hướng tư duy cho các em khi gặp các bài tập nâng cao, mang tính phân hóa cao từ đó khi vào trắc nghiệm các em biết cách làm nhanh các câu hỏi liên quan đến chủ đề này.

TẢI XUỐNG↓

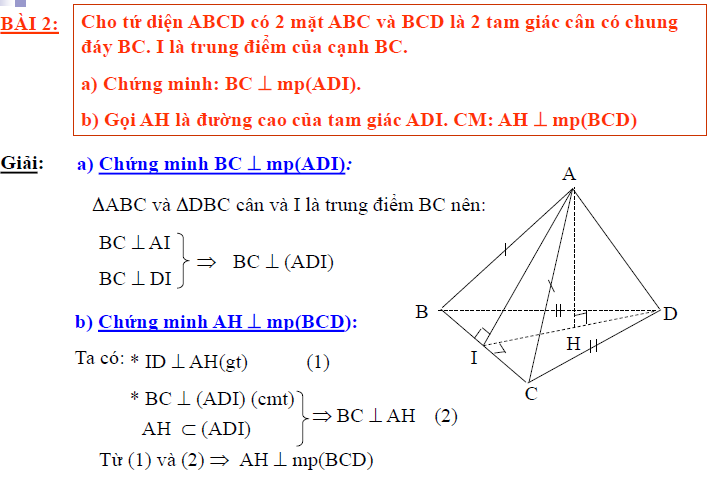
BÀI 2: Cho tứ diện ABCD có 2 mặt ABC và BCD là 2 tam giác cân có chung đáy BC. I là trung điểm của cạnh BC.

a) Chứng minh: BC ⊥mp(ADI). b) Gọi AH là đường cao của tam giác ADI. CM: AH ⊥ mp(BCD)

Giải:

a) Chứng minh BC ⊥ mp(ADI):

ΔABC và ΔDBC cân và I là trung điểm BC nên: BC ⊥ AI BC ⊥ DI

⇒ BC ⊥ (ADI)

b) Chứng minh AH ⊥ mp(BCD): Ta có: * ID ⊥AH(gt) (1) * BC ⊥(ADI) (cmt) ⇒BC ⊥AH và  AH ⊂ (ADI) (2) Từ (1) và (2) ⇒ AH ⊥ mp(BCD)

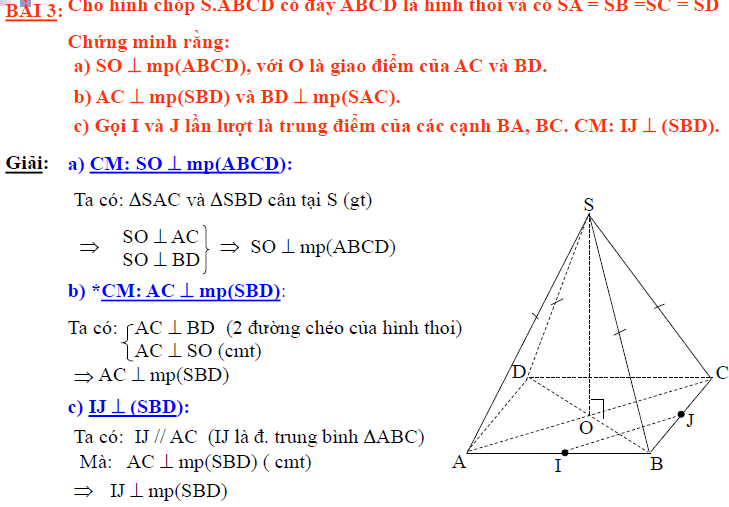
BÀI 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi và có SA = SB =SC = SD

Chứng minh rằng:

a) SO ⊥ mp(ABCD), với O là giao điểm của AC và BD.

b) AC ⊥ mp(SBD) và BD ⊥ mp(SAC).

c) Gọi I và J lần lượt là trung điểm của các cạnh BA, BC. CM: IJ ⊥ (SBD).

Giải

a) CM: SO  mp(ABCD): Ta có: ΔSAC và ΔSBD cân tại S (gt)

⇒SO ⊥ AC và SO ⊥ BD

⇒ SO ⊥ mp(ABCD)

b) *CM: AC ⊥ mp(SBD)

Ta có: AC ⊥ BD (2 đường chéo của hình thoi) và AC ⊥SO (cmt) ⇒AC ⊥ mp(SBD) c) IJ ⊥ (SBD):

Ta có: IJ // AC (IJ là đ. trung bình ΔABC) Mà: AC ⊥ mp(SBD) ( cmt) ⇒ IJ ⊥ mp(SBD)

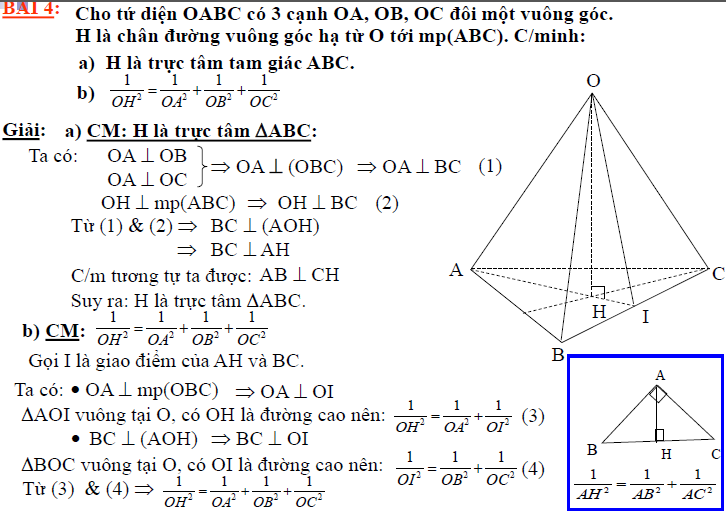
BÀI 4:Cho tứ diện OABC có 3 cạnh OA, OB, OC đôi một vuông góc.H là chân đường vuông góc hạ từ O tới mp(ABC). C/minh: a) H là trực tâm tam giác ABC.

                                    b) 1/ OH² = 1/ OA² + 1/OB² + 1/OC²

Giải:

a) CM: H là trực tâm ΔABC:

Ta có: OA ⊥OB  và OA ⊥ OC ⇒ OA ⊥ (OBC)⇒ OA ⊥ BC   (1)

OH ⊥ mp(ABC) ⇒ OH ⊥ BC (2) Từ (1)& (2) ⇒ BC ⊥ (AOH) ⇒ BC ⊥ AH C/m tương tự ta được: AB ⊥ CH Suy ra: H là trực tâm ΔABC. b) CM: 1/ OH² = 1/ OA² + 1/OB² + 1/OC²

Gọi I là giao điểm của AH và BC. Ta có: ♥ OA ⊥ mp(OBC) ⇒ OA ⊥OI ⇒ΔAOI vuông tại O, có OH là đường cao nên: 1/ OH² = 1/ OA² + 1/ OI² ( 3) ♥  BC ⊥(AOH) ⇒ BC ⊥ OI ⇒ΔBOC vuông tại O, có OI là đường cao nên: 1/ OI² = 1/ OB² + 1/ OC² (4)

Từ 3 & 4 ⇒ 1/ OH² = 1/ OA² + 1/OB² + 1/OC²

Bài 6: Cho hình chóp S.ABCD, có đáy là hình thoi ABCD và có cạnh SA vuông góc với mp(ABCD). Gọi I và K là 2 điểm lấy trên 2 cạnh SB và SD sao cho SI/SB = SD/ SD.

Chứng minh: a) BD ⊥ SC b) IK ⊥ mp(SAC)

Giải :  a) BD ⊥ SC

BD ⊥ AC (2 đường chéo hình thoi) BD ⊥ SA (SA ⊥ (ABCD) ⇒ BD ⊥ (SAC) ⇒ BD ⊥ SC

b) IK ⊥ (SAC):

Ta có: SI/SB = SD/ SD⇒ IK // BD

Mà BD ⊥ (SAC)  ⇒ IK ⊥ (SAC)

Ra thêm 1) Cho tứ diện ABCD. CMR nếu AB ⊥ CD, AC ⊥ BD thì BC ⊥AD.

Giải:

Gọi H là hình chiếu của A trên mặt phẳng (BCD). Suy ra BH và CH lần lượt là hình chiếu của AB và AC trên mp(BCD).

Ta có:*CD ⊥ AB ⇒CD ⊥ BH (Đlí 3 đường vuông góc) *BD ⊥ AC ⇒ BD ⊥ CH (Đlí 3 đường vuông góc) Vậy H là trực tâm tam giác BCD. Suy ra: BC ⊥ DH Mà DH là hình chiếu của AD trên mp(BCD) nên BC⊥AD.

BÀI 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, mặt bên (SAB) là tam giác đều và SC = a√2. Gọi H và K lần lượt là trung điểm của các cạnh AB và AD. a) Chứng minh rằng: SH ⊥ (ABCD). b) Chứng minh: AC ⊥ SK và CK ⊥ SD.

Hướng dẫn:

a) CM: SH ⊥(ABCD): ♦Dùng đl đảo đl Pitago cm: BC ⊥ SB ♦BC ⊥ AB (ABCD là hình vuông) ⇒ BC ⊥ (SAB) ⇒ BC ⊥SH (1) Mặt khác: AB ⊥SH (2) Từ (1) và (2) ⇒ SH ⊥ (ABCD

b) CM AC ⊥ SK và CK ⊥ SD:

♦ CM AC ⊥ SK

Ta có:  HK // DB và  AC⊥  DB⇒ HK ⊥AC (1)

SH ⊥ (ABCD) và  AC ⊂ (ABCD) ⇒SH ⊥AC (2) Từ (1) & (2) ⇒ AC ⊥(SHK) ⇒ AC ⊥SK

♦ CM CK ⊥ SD:

Ta cm được: CK ⊥ DH (1) SH⊥ (ABCD) và  CK ⊥ (ABCD)⇒ CK ⊥ SH (2) Từ (1) & (2) ⇒ CK ⊥ SD.

Bài tập về nhà

Dưới đây là một số bài tập về đường thẳng vuông góc với mặt phẳng, các em có thể làm ở nhà để  có thêm nhiều kiến thức nhé.

Cho hình chóp S.ABCD, đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều; SCD là tam giác vuông cân đỉnh S. Gọi I và J lần lượt là trung điểm của AB và CD. a) Tính các cạnh của tam giác SIJ. b) Chứng minh SI ⊥ (SCD) và SJ ⊥ (SAB). c) Gọi H là hình chiếu vuông góc của S trên IJ. Chứng minh: SH ⊥ AC.

Cảm ơn các em đã xem và tải tài liệu bài tập về đường thẳng vuông góc với mặt phẳng. Chúng tôi mong rằng những bài tập này sẽ hữu ích với các em trong việc tìm hiểu hình học không gian. Ngoài ra các em cần phải làm thật nhiều bài  tập để có thêm kiến thức cũng như tập phản xạ nhé.