Bài Tập Xác Suất Lớp 11 Có đáp án

Bài tập xác suất lớp 11 có đáp ánBài tập Toán lớp 11 có đáp án Tải về Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi. Mua ngay Từ 79.000đ Tìm hiểu thêm

Bài tập xác suất lớp 11 có đáp án

Bài tập xác suất lớp 11 có đáp án là tài liệu hữu ích dành cho các bạn học sinh lớp 11 và các bạn ôn thi đại học củng cố kiến thức về tổ hợp xác xuất. Mời các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây nhé.

Bài toán 1.

Cho một lục giác đều ABCDEF. Viết các chữ cái A, B, C, D, E, F vào 6 thẻ. Lấy ngẫu nhiên hai thẻ. Tìm xác suất sao cho đoạn thẳng mà các đầu mút là các điểm được ghi trên 2 thẻ đó là:

a) Cạnh của lục giác.

b) Đường chéo của lục giác.

c) Đường chéo nối 2 đỉnh đối diện của lục giác.

(Bài 8 – trang 77 sách Đại số và giải tích 11)

Giải:

• Vì lấy 2 điểm nên: C26 = 15 -> n(Ω) = 15.
• Gọi:
• A là biến cố "2 thẻ lấy ra là 2 cạnh của lục giác"
• B là biến cố "2 thẻ lấy ra là đường chéo của lục giác"
• C là biến cố "2 thẻ lấy ra là đường chéo của 2 cạnh đối diện của lục giác"

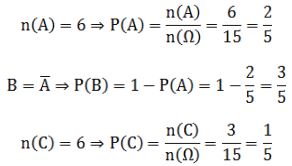
Bài toán 2.

Xếp ngẫu nhiên ba bạn nam và ba bạn nữ ngồi vào sáu ghế kê theo hàng ngang. Tìm xác suất sao cho.

a) Nam nữ ngồi xen kẽ nhau.

b) Ba bạn nam ngồi cạnh nhau.

(Bài 6 – trang 76 sách Đại số và giải tích 11)

Giải:

• Cách xếp 3 bạn nam và 3 bạn nữ vào 6 ghế kê theo hàng ngang 6! = 720 cách.
• Cách xếp 3 bạn nam và 3 bạn nữ vào 6 ghế kê theo hàng ngang, biết rằng nam nữ ngồi xen kẽ nhau 3!.3! + 3!.3! = 72 cách.
• Cách xếp 3 bạn nam và 3 bạn nữ vào 6 ghế kê theo hàng ngang, biết rằng ba bạn nam ngồi cạnh nhau 4.3!.3! = 144 cách.
• Gọi là biến cố "Xếp 3 học sinh nam và 3 học sinh nữ vào 6 ghế kê theo hàng ngang mà nam và nữ xen kẽ nhau"
• Gọi là biến cố "Xếp 3 học sinh nam và 3 học sinh nữ vào 6 ghế kê theo hàng ngang mà 3 bạn nam ngồi cạnh nhau"
• Ta có n(Ω) = 720, n(A) = 72, n(B) = 144
• Suy ra

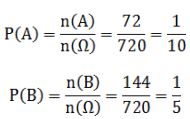
Bài toán 3.

Gieo một con súc xắc, cân đối và đồng nhất. Giả sử con súc xắc suất hiện mặt b chấm. Xét phương trình x2 + bx + 2 = 0. Tính xác suất sao cho phương trình có nghiệm.

(Bài 4 trang 74 sách Đại số và giải tích 11)

Giải

• Ký hiệu "con súc xắc suất hiện mặt b chấm" là b:
• Không gian mẫu: Ω = {1; 2; 3; 4; 5; 6} → n(Ω) = 6
• Gọi A là biến cố: "Phương trình có nghiệm"
• Ta đã biết phương trìnhx2 + bx + 2 = 0 có nghiệm khi Δ = b2 - 8 ≥ 0
• Do đó: A = {b ∈ Ω | b2 - 8 ≥ 0} = {3; 4; 5; 6} → n(A) = 4

Bài toán 4.

Trên một cái vòng hình tròn dùng để quay sổ số có gắn 36 con số từ 01 đến 36. Xác suất để bánh xe sau khi quay dừng ở mỗi số đều như nhau. Tính xác suất để khi quay hai lần liên tiếp bánh xe dừng lại ở giữa số 1 và số 6 ( kể cả 1 và 6) trong lần quay đầu và dừng lại ở giữa số 13 và 36 ( kể cả 13 và 36) trong lần quay thứ 2.

Giải

Phân tích: Rõ ràng là trong bài toán này ta không thể sử dụng phương pháp liệt kê vì số phần tử của biến cố là tương đối lớn. Ở đây ta sẽ biểu diễn tập hợp dưới dạng tính chất đặc trưng để tính toán.

Gọi A là biến cố cần tính xác suất:

Ω = {(i,j) Ι i,j ε {1, 2, ...., 36}} ===> n(Ω) = 36.36 = 1296

A = {(i,j) Ι i ε {1, 2, ...., 6}, j ε {13, 14, ...., 36}}

Có 6 cách chọn i, ứng với mỗi cách chọn i có 25 cách chọn j ( từ13 đến36 có 25 số) do đó theo quy tắc nhân n(A) = 6.24 = 144

P(A) = n(A)/n(Ω) = 144/1296 = 1/9

Bài toán 5

Gieo một đồng tiền cân đối đồng chất liên tiếp cho đến khi lần đầu tiên xuất hiện mặt ngửa hoặc cả 6 lần xuất hiện mặt sấp thì dừng lại.

a) Mô tả không gian mẫu.

b) Tính xác suất:

A: “Số lần gieo không vượt quá ba”

B: “Số lần gieo là năm”

C: “Số lần gieo là sáu”

a) Không gian mẫu Ω = {N, SN, SSN, SSSN, SSSSN, SSSSS}

b) Ta có:

A = {N, SN, SSN}, n(A) = 3 => P(A) = 3/7

B = {SSSSN}, n(B) = 1 => P(B) = 1/7

C = {SSSSSN, SSSSSS} n(C) = 2 => P(C) = 2/7

Bài toán 6

Gieo đồng tiền xu cân đối đồng chất 3 lần. Tính xác suất của các biến cố:

a) Biến cố A: “Trong 3 lần gieo có ít nhất một lần xuất hiện mặt ngửa”.

b) Biến cố B: “Trong 3 lần gieo có cả hai mặt sấp, ngửa”.

Giải+ Không gian mẫu n(Ω) = 2.2.2 = 8

+ Ta có biến cố đối của biến cố A là biến cố:

A: “Không cố lần nào xuất hiện mặt ngửa”

Và ta có A = {SSS} => n(A) = 1 => P(A) = 1/8 => P(A) = 1 - 1/8 = 7/8

Tương tự ta có:

B = {SSS, NNN} => n(B) = 2 => P(B) = 1/4 => P(B) = 3/4

Bài toán 7.

Gieo ngẫu nhiên một con súc sắc cân đối đồng chất hai lần. Tính xác suất của các biến cốsau:

a) Biến cố A: “Trong hai lần gieo ít nhất một lần xuất hiện mặt một chấm”

b) Biến cố B: “Trong hai lần gieo tổng số chấm trong hai lần gieo là một số nhỏ hơn 11”

Bài toán 8.

Gieo đồng thời hai con súc sắc. Tính xác suất sao cho:

a) Hai con súc sắc đều xuất hiện mặt chẵn.

b) Tích số chấm trên 2 con súc sắc là số chẵn.

Bài tập xác suất trắc nghiệm

Câu 1: Gieo đồng tiền 5 lần cân đối và đồng chất. Xác suất để được ít nhất một lần xuất hiện mặt sấp là:

A. 31/32

B. 21/32

C. 11/32

D. 1/32

Câu 2: Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A: “có đúng 2 lần xuất hiện mặt sấp”.

A. P(A)=1/2

B. P(A)=3/8

C. P(A)=7/8

D. P(A)=1/4

Câu 3: Một hộp có 5 viên bi​​ xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng.

A.​​ 313/408.

B.​​ 95/408. 

C.​​ 5/102.

D.​​ 25/136.

Câu 4: Một hộp có 5 viên bi đỏ, 3 viên bi vàng và 4 viên bi xanh. Chọn ngẫu nhiên từ​​ hộp 4 viên bị, tính xác suất để 4 viên bi được chọn có số bi đỏ lớn hơn số bi vàng và nhất thiết phải có mặt bi xanh.

A.​​ 1/12.

B.​​ 1/3.

C.​​ 16/33.

D.​​ 1/2.

Câu 5: Có 3 bó hoa. Bó thứ nhất có 8 hoa hồng, bó thứ hai có 7 bông hoa ly, bó thứ ba có 6 bông hoa huệ. Chọn ngẫu nhiên 7 hoa từ ba bó hoa trên để cắm vào lọ hoa, tính xác suất để trong 7 hoa được chọn có số hoa hồng bằng số hoa ly.

A.​​ 3851/4845

B.​​ 1/71

C.​​ 36/71

D.​​ 994/4845

Mời các bạn tải file đầy đủ về tham khảo!

Trên đây VnDoc.com vừa giới thiệu tới các bạn Bài tập xác suất lớp 11 có đáp án. Bài viết được tổng hợp các bài toán xác suất dạng tự luận và bài toán xác suất dạng trắc nghiệm... Mong rằng qua bài viết này các bạn có thể học tập tốt hơn môn Toán lớp 11. Mời bạn đọc cùng tham khảo thêm mục Trắc nghiệm Toán 11...

• Tài liệu ôn thi THPT Quốc gia môn Toán: Tuyển chọn 50 bài toán Xác suất điển hình
• 20 bộ đề thi học kì 1 môn Toán lớp 11
• Bộ đề kiểm tra giữa học kì 1 môn Toán lớp 11