Bất đẳng Thức Cauchy Schwarz Và Bài Tập ứng Dụng Có Giải
Có thể bạn quan tâm
Tóm tắt tài liệu
- Cách dùng bất đẳng thức cauchy – schwartz (BCS)
- Bất đăng thức cauchy – schwartz dạng engel (dạng phân thức)
- Chứng minh bất đẳng thức Cauchy–Schwarz dạng Engel
- Ứng dụng bất đẳng thức C.S dạng Engel vào các bài toán điển hình
- Bài tập ứng dụng C.S có lời giải
Trong toán học, bất đẳng thức Cauchy Schwarz, còn được gọi là bất đẳng thức Schwarz , bất đẳng thức Cauchy , hoặc bằng cái tên khá dài là bất đẳng thức Cauchy – Bunyakovski – Schwarz. Loại bất đẳng thức này là một bất đẳng thức thường được áp dụng trong nhiều lĩnh vực khác nhau của toán học, chẳng hạn trong đại số tuyến tính dùng cho các vector, trong giải tích dùng cho các chuỗi vô hạn và tích phân của các tích, trong lý thuyết xác suất dùng cho các phương sai và hiệp phương sai. Để tìm hiểu tài liệu này, chúng ta cùng xét một số tiêu điểm sau:
TẢI XUỐNG PDF ↓
TẢI XUỐNG PDF ↓
Cách dùng bất đẳng thức cauchy – schwartz (BCS)
Bất đẳng thức Cauchy Schwarz được dùng khá phổ biến trong các bài toán bất đẳng thức, tài liệu đầu tiên sẽ giúp các em hiểu rõ định lí gốc và một số cách ứng dụng bất đẳng thức này. Dưới đây là 5 dạng áp dụng bất đẳng thức cơ bản nhất, thường gặp nhất mà các bài toán thường nhắm đến, các em hãy cùng tìm hiểu để rút ra được kinh nghiệm cho mình
Xem thêm: Những viên kim cương trong bất đẳng thức toán học [PDF]
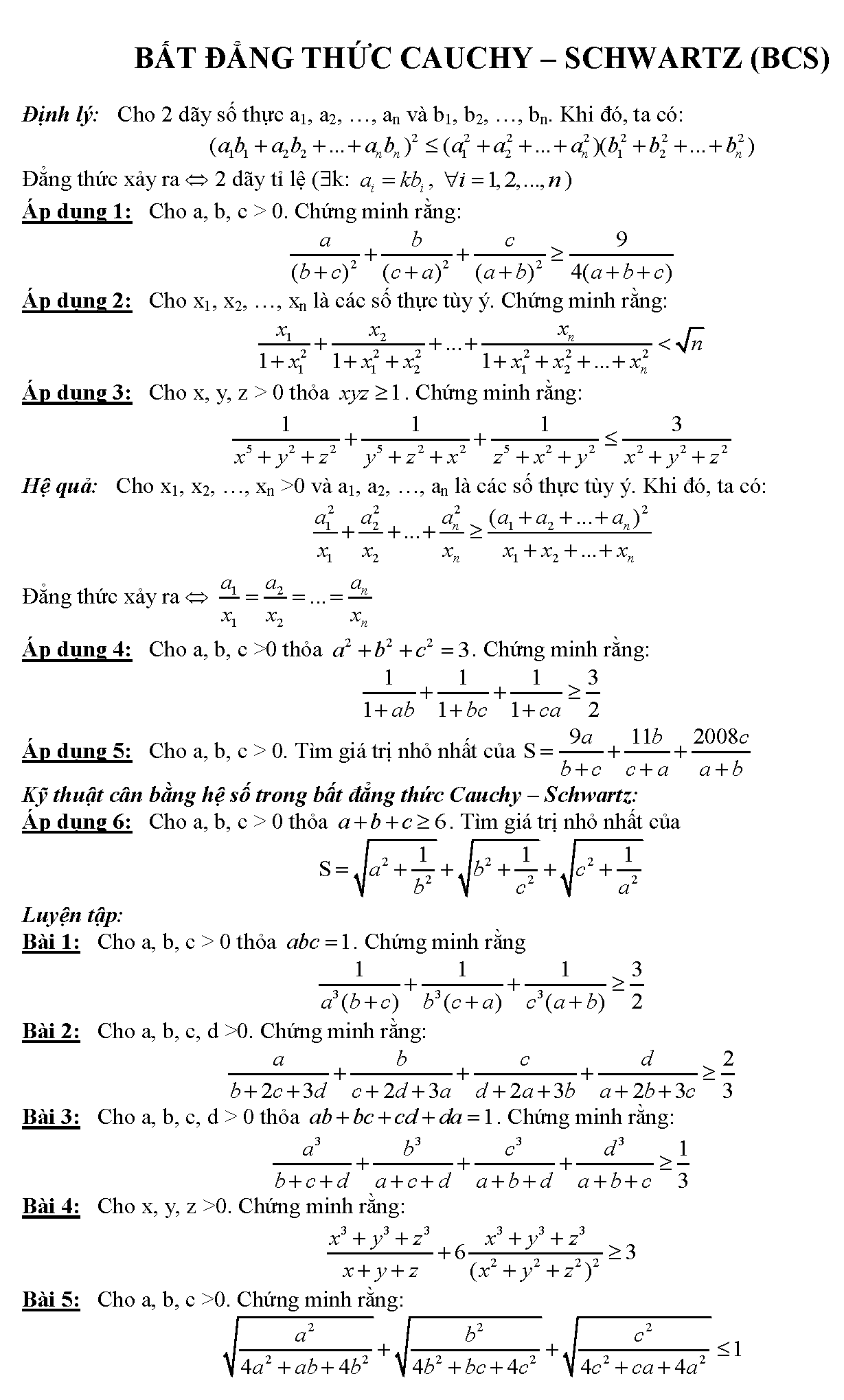
Bất đăng thức cauchy – schwartz dạng engel (dạng phân thức)
Đây là một mãng kiến thức khá hay về bất đẳng thức cauchy schwartz. Dưới dạng phân thức, bất đẳng thức này càng phát triển nhiều khả năng mà các bất đẳng thức khác không có.
Chứng minh bất đẳng thức Cauchy–Schwarz dạng Engel
Phương pháp chứng minh đi từ những bất đẳng thức cơ bản nhất và bằng phương pháp qui nạp toán học. Phải nói rằng đây là phương pháp hay dùng nhất để chứng minh bất kì bất đẳng thức nào. Xem sơ qua phương pháp chứng minh để cho biết chứ không cần ghi nhớ. Cái mà chúng ta phải quan tâm đó chính là kĩ thuật sử dụng, trường hợp áp dụng.
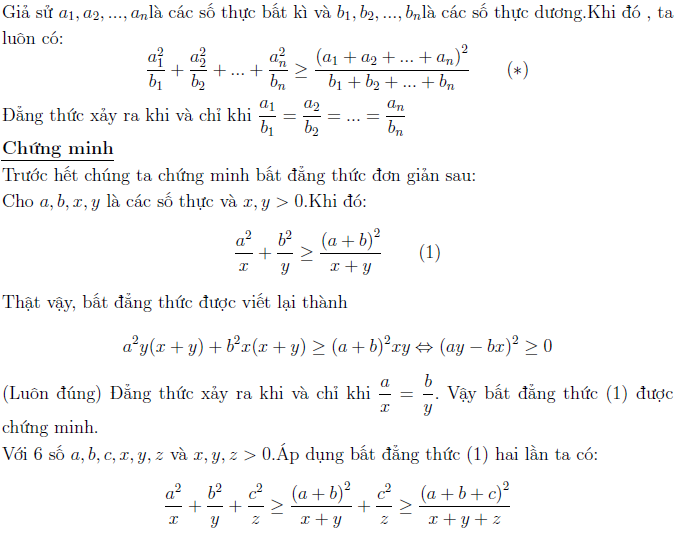
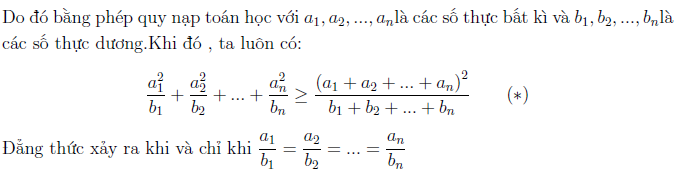
Ứng dụng bất đẳng thức C.S dạng Engel vào các bài toán điển hình
Việc ứng dụng vào các bài toán điển hình giúp rèn luyện tư duy cũng như phản xạ. Các bài toán điển hình thường đi rất sát với các bất đẳng thức. Tức là chỉ dùng bất đẳng thức này thì bài toán mới giải quyết một cách nhanh chóng. Từ đó giúp các học sinh dễ dàng nhận biết được những bài tập nào với dấu hiệu ra sao có thể áp dụng bất đẳng thức đó.


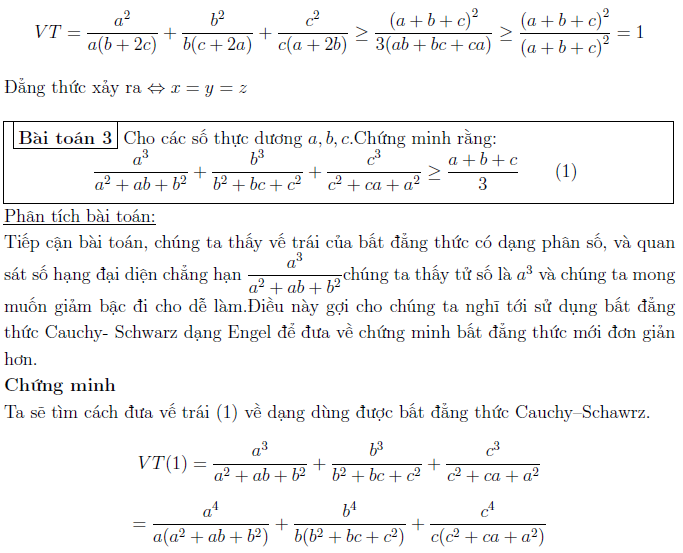
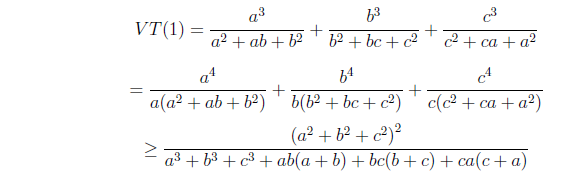

Bài tập ứng dụng C.S có lời giải
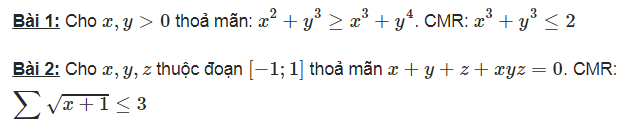
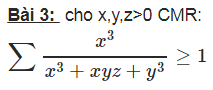
Đáp án Bài 1
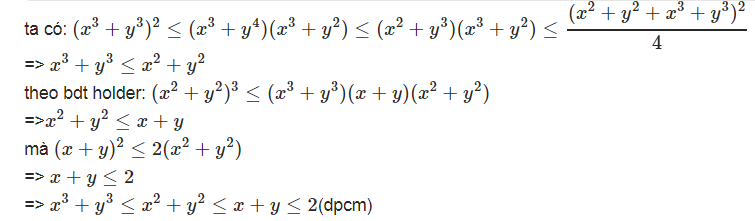
Đáp án bài 3:
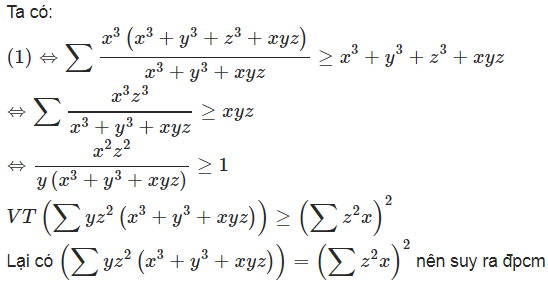
Vậy là chúng ta vừa tìm hiểu xong bất đẳng thức cauchy schwarz. Nếu bạn còn thắc mắc gì về phương pháp giải cũng như các ví dụ trong các tài liệu, có thể để lại bình luận phía dưới. Bất đẳng thức là một chuyên đề khá khó, do đó để đạt được kết quả cao các em cần phải rèn luyện thật nhiều bài tập cũng như luyện tập tư duy sáng tạo, phản xạ.
Xem thêm bất đẳng thức bernoulli
Từ khóa » định Luật Bcs
-
Những Kiến Thức Cơ Bản Về Bất đẳng Thức Bunhiacopxki - VOH
-
Bất đẳng Thức Bunhiacopxki: Công Thức, Cách Chứng Minh Và Bài Tập ...
-
Lý Thuyết BCS – Wikipedia Tiếng Việt
-
Công Thức Bất đẳng Thức Bunhiacopxki - CungHocVui
-
Bất đẳng Thức Bunhiacopxki - Chuyên đề Toán Lớp 9 Luyện Thi Vào ...
-
Ký Hiệu BCS Là đất Gì? Các Quy định Về đất BCS - Homedy
-
Chứng Minh Bất đẳng Thức Bunhiacopxki Kèm Ví Dụ Minh Họa
-
Nhập Khẩu Và Lưu Hành Bao Cao Su - AZLAW
-
Quyết định 2177/QĐ-BYT Chương Trình Tổng Thể Bao Cao Su Tại Việt ...
-
Điều Kiện đăng Ký Mở Cửa Hàng Bán Bao Cao Su - Luật Sư X
-
Bao Cao Su Có Phải Mặt Hàng Thiết Yếu Theo Chỉ Thị Số 16 Không?
-
VIVA Business Consulting | Tư Vấn & Kinh Doanh | Trang Chủ
-
Được Quảng Cáo Bao Cao Su, Băng Vệ Sinh Trong Khung Giờ Vàng