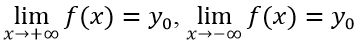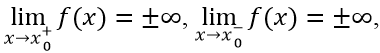Các Bài Toán đường Tiệm Cận Của đồ Thị Hàm Số

Nội dung bài viết

1. Lý thuyết đường tiệm cận
   1. Định nghĩa đường tiệm cận ngang
   2. Định nghĩa đường tiệm cận đứng
   3. Định nghĩa đường tiệm cận xiên
   4. Phương pháp giải các dạng toán tìm tiệm cận của đồ thị hàm số chuẩn nhất
2. Các dạng bài tập tìm tiệm cận của đồ thị hàm số
   1. Dạng 1. Xác định đường tiệm cận thông qua bảng biến thiên
   2. Dạng 2. Xác định đường tiệm cận đồ thị hàm số thông hàm số cho trước
   3. Dạng 3. Định m để đồ thị hàm số có đường tiệm cận thỏa mãn điều kiện cho trước
   4. Dạng 4. Xác định tiệm cận của đồ thị hàm số g[f(x)] khi biết bảng biến thiên hàm số f(x)

Tổng hợp đầy đủ các dạng bài tập, câu hỏi trắc nghiệm về chủ đề tìm tiệm cận của đồ thị hàm số có đáp án và hướng dẫn giải chi tiết nhằm giúp các em học sinh củng cố kiến thức và giải thành thạo dạng toán này.

Lý thuyết đường tiệm cận

Tóm tắt kiến thức cơ bản lý thuyết tìm tiệm cận của đồ thị hàm số trong chương trình trung học phổ thông môn toán:

Định nghĩa đường tiệm cận ngang

Cho hàm số y = f(x) xác định trên một khoảng vô hạn (là khoảng dạng (a; +∞),(-∞; -b) hoặc (-∞; +∞). Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn

 Nhận xét: Như vậy để tìm tiệm cận ngang của đồ thị hàm số ta chỉ cần tính giới hạn của hàm số đó tại vô cực. Những hàm thường gặp là hàm phân thức với bậc của tử không lớn hơn bậc của mẫu.

Định nghĩa đường tiệm cận đứng

Đường thẳng x = x0 được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn

Định nghĩa đường tiệm cận xiên

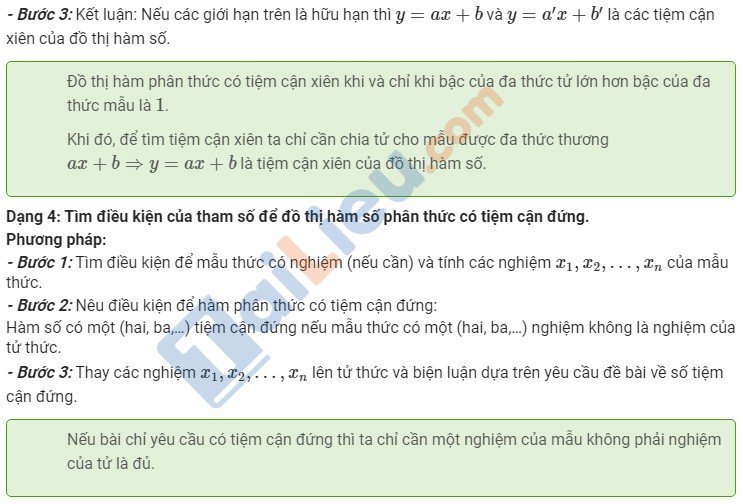
Phương pháp giải các dạng toán tìm tiệm cận của đồ thị hàm số chuẩn nhất

Làm thế nào để xác định tiệm cận đứng tiệm cận ngang trên bảng biến thiên hay cách tìm tiệm cận trên bảng biến thiên đơn giản nhất ra sao? Mời các bạn tham khảo ngay một số phương pháp giải ngắn gọn, nhanh chóng dưới đây:

Các dạng bài tập tìm tiệm cận của đồ thị hàm số

Dưới đây là tuyển chọn 59 câu hỏi trắc nghiệm được chọn lọc từ các đề thi tốt nghiệp THPT các năm và đề thi thử, đề minh họa của các trường cấp 3 các tỉnh thành trên cả nước tổng hợp theo 4 dạng toán tìm tiệm cận của đồ thị hàm số phổ biến nhất.

Trong mỗi dạng bài tập cách tìm tiệm cận qua bảng biến thiên, tìm đường tiệm cận đồ thị hàm số thông hàm số...vv chúng tôi sẽ trích dẫn một vài câu hỏi mẫu, mời các bạn theo dõi toàn bộ nội dung 59 câu hỏi cùng đáp án và lời giải chi tiết tại file tải về miễn phí sau:

Dạng 1. Xác định đường tiệm cận thông qua bảng biến thiên

Dưới đây là các bài toán cách xác định tiệm cận qua bảng biến thiên hay còn gọi là dạng toán cho bảng biến thiên tìm số tiệm cận

Dạng 2. Xác định đường tiệm cận đồ thị hàm số thông hàm số cho trước

Dạng 3. Định m để đồ thị hàm số có đường tiệm cận thỏa mãn điều kiện cho trước

Dạng 4. Xác định tiệm cận của đồ thị hàm số g[f(x)] khi biết bảng biến thiên hàm số f(x)

Trên đây là nội dung tổng hợp lý thuyết về tiệm cận ngang, tiệm cận đứng, tiệm cận xiên và các dạng bài toán tìm tiệm cận của đồ thị hàm số có file download miễn phí giúp các em học sinh ôn luyện thành thạo dạng toán này.

Cùng chia sẻ nội dung hữu ích này cho bạn bè và người thân cùng tham khảo và sử dụng nhé.