Các Dạng Bài Tập Toán Về Mệnh đề Và Phương Pháp Giải - Toán Lớp 10
Có thể bạn quan tâm
Mệnh đề và tập hợp nằm trong chương mở đầu của sách giáo khoa đại số toán 10, để học tốt toán 10 các em cần nắm vững kiến thức ngay từ bài học đầu tiên. Vì vậy trong bài viết này chúng ta cùng ôn lại kiến thức Mệnh đề và áp dụng giải một số bài tập.
» Đừng bỏ lỡ: Các dạng toán về Tập hợp cực hay
I. Lý thuyết về Mệnh đề
1. Mệnh đề là gì?
- Định nghĩa: Mệnh đề là một câu khẳng định ĐÚNG hoặc SAI.
- Một mệnh đề không thể vừa đúng hoặc vừa sai.
2. Mệnh đề phủ định
- Cho mệnh đề  , mệnh đề "không phải
, mệnh đề "không phải  " gọi là mệnh đề phủ định của phủ định của
" gọi là mệnh đề phủ định của phủ định của  , ký hiệu là
, ký hiệu là 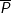 .
.
- Nếu  đúng thì
đúng thì 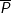 sai, nếu
sai, nếu  sai thì
sai thì 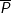 đúng.
đúng.
3. Mệnh đề kéo theo và mệnh đề đảo
- Cho hai mệnh đề  và
và 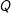 , mệnh đề "nếu
, mệnh đề "nếu  thì
thì 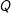 " gọi là mệnh đề kéo theo, ký hiệu là
" gọi là mệnh đề kéo theo, ký hiệu là  ⇒
⇒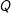 .
.
- Mệnh đề  ⇒Q sai khi
⇒Q sai khi  đúng
đúng 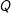 sai.
sai.
- Cho mệnh đề  ⇒
⇒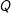 , khi đó mệnh đề
, khi đó mệnh đề 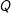 ⇒
⇒ gọi là mệnh đề đảo của
gọi là mệnh đề đảo của  ⇒
⇒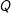 .
.
- Nếu  ⇒Q đúng thì:
⇒Q đúng thì:
◊ P là điều kiện ĐỦ để có Q
◊ Q là điều kiện CẦN để có P
4. Mệnh đề tương đương
- Cho hai mệnh đề  và
và 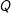 , mệnh đề "
, mệnh đề " nếu và chỉ nếu
nếu và chỉ nếu 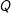 " gọi là mệnh đề tương đương, ký hiệu là
" gọi là mệnh đề tương đương, ký hiệu là  ⇔
⇔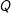 .
.
- Mệnh đề  ⇔
⇔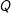 đúng khi cả
đúng khi cả  ⇒
⇒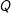 và
và 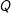 ⇒
⇒ cùng đúng.
cùng đúng.
* Chú ý: "Tương đương" còn được gọi bằng các thuật ngữ khác như "điều kiện cần và đủ", "khi và chỉ khi", "nếu và chỉ nếu".
5. Mệnh đề chứa biến
- Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập X nào đó mà với mỗi giá trị của biến thuộc X ta được một mệnh đề.
6. Các kí hiệu ∀, ∃ và mệnh đề phủ định của mệnh đề có chứa kí hiệu ∀, ∃
- Kí hiệu ∀ : đọc là với mọi; ký hiệu ∃ đọc là tồn tại.
- Phủ định của mệnh đề 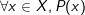 là mệnh đề
là mệnh đề 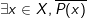 .
.
- Phủ định của mệnh đề 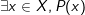 là mệnh đề
là mệnh đề 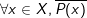 .
.
II. Các dạng bài tập toán về Mệnh đề và phương pháp giải
• Dạng 1: Xác định mệnh đề và tính đúng sai của mệnh đề
* Phương pháp:
- Dựa vào định nghĩa mệnh đề xác định tính đúng sai của mệnh đề đó
- Mệnh đề chứa biến: Tìm tập D của các biến x để p(x) đúng hoặc sai
Ví dụ 1: Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề? Nếu là mệnh đề hãy cho biết mệnh đề đó đúng hay sai.
a) Trời hôm nay đẹp quá!
b) Phương trình x2 - 3x +1 = 0 vô nghiệm.
c) 15 không là số nguyên tố.
d) Hai phương trình x2 - 4x + 3 = 0 và 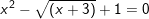 có nghiệm chung.
có nghiệm chung.
e) Số Π có lớn hơn 3 hay không?
f) Italia vô địch Worldcup 2006.
g) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.
h) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.
* Hướng dẫn:
- Câu a) câu e) không là mệnh đề (là câu cảm thán, câu hỏi?)
- Câu c) d) f) h) là mệnh đề đúng
- Câu b) câu g) là mệnh đề sai
Ví dụ 2: Xác định tính đúng sai của các mệnh đề sau
a) 2 là số chẵn
b) 2 là số nguyên tố
c) 2 là số chính phương
* Hướng dẫn:
a) Đúng
b) Đúng (2 chia hết cho 1 và chính nó nên là số nguyên tố)
c) Sai (số chính phương có các chữ số tận cùng là 0, 1, 4, 5, 6, 9)
Ví dụ 3: Điều chính ký hiệu ∀ và ∃ để được mệnh đề đúng
a) ∀x ∈ R: 2x + 5 = 0
b) ∀x ∈ R: x2 - 12 = 0
* Hướng dẫn:
a) ∃x ∈ R: 2x + 5 = 0
b) ∃x ∈ R: x2 - 12 = 0
• Dạng 2: Các phép toán về mệnh đề - phủ định mệnh đề
* Phương pháp: Dựa vào định nghĩa các phép toán
+) 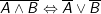
+) 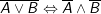
+) 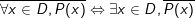
+) 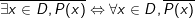
Ví dụ 1: Nêu mệnh đề phủ định của các mệnh đề sau, cho biết mệnh đề này đúng hay sai?
P: "Hình thoi có hai đường chéo vuông góc với nhau".
Q: "66 là số nguyên tố".
R: Tổng hai cạnh của một tam giác lớn hơn cạnh còn lại
S: "3>-2"
K: "Phương trình x4 - 2x2 + 2 = 0 có nghiệm"
H: 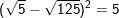
* Hướng dẫn:
- Ta có mệnh đề phủ định là:
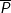 : "Hai đường chéo của hình thoi không vuông góc với nhau"; mệnh đề này SAI
: "Hai đường chéo của hình thoi không vuông góc với nhau"; mệnh đề này SAI
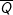 : "66 không phải là số nguyên tố"; mệnh đề này ĐÚNG
: "66 không phải là số nguyên tố"; mệnh đề này ĐÚNG
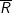 : "Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại", mệnh đề này SAI
: "Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại", mệnh đề này SAI
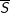 : "3≤-2"; mệnh đề này SAI
: "3≤-2"; mệnh đề này SAI
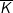 : "Phương trình x4 - 2x2 + 2 = 0 vô nghiệm"; mệnh đề này SAI
: "Phương trình x4 - 2x2 + 2 = 0 vô nghiệm"; mệnh đề này SAI
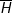 :
: 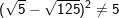 ; mệnh đề này ĐÚNG
; mệnh đề này ĐÚNG
Ví dụ 2: Phủ định của các mệnh đề sau
A: n chia hết cho 2 và chia hết cho 3 thì n chia hết cho 6.
B: ΔABC vuông cân tại A
C: √2 là số thực
* Hướng dẫn:
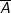 : n không chia hết cho 2 hoặc không chia hết cho 3 thì n không chia hết cho 6.
: n không chia hết cho 2 hoặc không chia hết cho 3 thì n không chia hết cho 6.
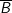 : ΔABC không vuông cân tại A ⇔ ΔABC không vuông hoặc không cân tại A.
: ΔABC không vuông cân tại A ⇔ ΔABC không vuông hoặc không cân tại A.
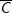 : √2 không là số thực ⇔
: √2 không là số thực ⇔ 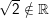
Ví dụ 3: Phủ định của các mệnh đề sau và cho biết tính đúng sai.
P: ∀x ∈ R: x2 + 2 > 0
Q: ∃x ∈ R: x3 + x2 + x + 2 ≠ 0
R: ∀A, ∀B: A∩B⊂A
* Hướng dẫn:
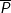 : ∃x ∈ R: x2 + 2 ≤ 0 ; mệnh đề này SAI
: ∃x ∈ R: x2 + 2 ≤ 0 ; mệnh đề này SAI
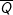 : ∀x ∈ R: x3 + x2 + x + 2 = 0 ; mệnh đề này SAI
: ∀x ∈ R: x3 + x2 + x + 2 = 0 ; mệnh đề này SAI
R: ∀A, ∀B: A∩B⊂A ⇔ ∀x∈A∩B ⇒x∈A
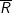 : ∃x∈A∩B⇒x∉A ; mệnh đề này SAI
: ∃x∈A∩B⇒x∉A ; mệnh đề này SAI
• Dạng 3: Các phép toán về mệnh đề - mệnh đề kéo theo, tương đương
* Phương pháp: Dựa vào định nghĩa các phép toán
+) 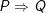 ; chỉ SAI khi
; chỉ SAI khi  đúng
đúng 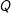 sai
sai
+) 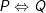 ; chỉ ĐÚNG nếu A và B cùng đúng hoặc cùng sai
; chỉ ĐÚNG nếu A và B cùng đúng hoặc cùng sai
Ví dụ 1: Phát biểu mệnh đề P ⇒ Q và phát biểu mệnh đề đảo, xét tính đúng sai của nó.
a) P:" Tứ giác ABCD là hình thoi" và Q: "Tứ giác ABCD có AC và BD cắt nhau tại trung điểm của mỗi đường".
b) P:"2>9" và Q: "4<3"
c) P:"Tam giác ABC vuông cân tại A" và Q: "Tam giác ABC có 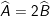 ".
".
* Hướng dẫn:
a) Mệnh đề: P ⇒ Q; P:"Tứ giác ABCD là hình thoi thì AC và BD cắt nhau tại trung điểm của mỗi đường". Là mệnh đề ĐÚNG
- Mệnh đề Đảo Q ⇒ P: "Tứ giác ABCD có AC và BD cắt nhau tại trung điểm của mỗi đường thì ABCD là hình thoi". Là mệnh đề SAI
b) Mệnh đề: P ⇒ Q: "Nếu 2>9 thì 4<3"; Là mệnh đề ĐÚNG
- Mệnh đề Đảo Q ⇒ P: "Nếu 4<3 thì 2>9 "; Là mệnh đề ĐÚNG
c) Mệnh đề: P ⇒ Q: "Nếu tam giác ABC vuông cân tại A thì 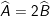 "
"
- - Mệnh đề Đảo Q ⇒ P: "Nếu tam giác ABC có 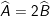 thì ABC là tam giác vuông cân tại A"; Là mệnh đề SAI.
thì ABC là tam giác vuông cân tại A"; Là mệnh đề SAI.
Ví dụ 2: Phát biểu mệnh đề P ⇔ Q và xét tính đúng sai.
a) P: "Tứ giác ABCD là hình thoi" và Q: "Tứ giác ABCD là hình bình hành có 2 đường chéo vuông góc với nhau"
b) P: "Bất phương trình 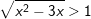 có nghiệm" và Q: "
có nghiệm" và Q: "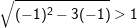 "
"
* Hướng dẫn:
a) P ⇔ Q: "Tứ giác ABCD là hình thoi khi và chỉ khi Tứ giác ABCD là hình bình hành và 2 đường chéo vuông góc với nhau". Là mệnh đề ĐÚNG vì P⇒Q đúng và Q⇒P đúng
b) P ⇔ Q: "Bất phương trình 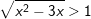 khi và chỉ khi
khi và chỉ khi 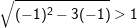 ". Là mệnh đề ĐÚNG vì P⇒Q đúng và Q⇒P đúng
". Là mệnh đề ĐÚNG vì P⇒Q đúng và Q⇒P đúng
• Dạng 4: Phương pháp chứng minh bằng phản chứng
* Phương pháp: Để chứng minh mệnh đề A đúng ta giả thiết 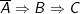 nếu C sai thì dừng phép chứng minh và kết luận A đúng.
nếu C sai thì dừng phép chứng minh và kết luận A đúng.
Ví dụ 1: Chứng minh "n2 chẵn ⇒ n chẵn"
* Hướng dẫn:
- Mệnh đề A: n chẵn
- 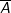 : n lẻ: ⇒ n = 2p + 1 (
: n lẻ: ⇒ n = 2p + 1 (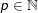 ) ⇒ n2 = (2p+1)2 = 4p2 + 4p + 1
) ⇒ n2 = (2p+1)2 = 4p2 + 4p + 1
⇒ n2 = 2(2p2 + 2p) + 1 ⇒ n2 = 2k + 1 (k = 2p2 + 2p)
⇒ n2 lẻ (trái giả thiết).
⇒ Vậy n chẵn.
Ví dụ 2: Chứng minh rằng: 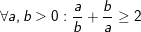
* Hướng dẫn:
- Giả sử: 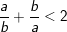 ⇒ a2 + b2 < 2ab ⇒ a2 + b2 - 2ab < 0 ⇒ (a-b)2<0 (Sai).
⇒ a2 + b2 < 2ab ⇒ a2 + b2 - 2ab < 0 ⇒ (a-b)2<0 (Sai).
- Vậy 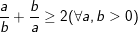
III. Bài tập về Mệnh đề
Bài 1 trang 9 sgk đại số 10: Trong các câu sau, câu nào là mệnh đề, câu nào là mệnh đề chứa biến?
a) 3 + 2 = 7 ; b) 4 + x = 3;
c) x + y > 1 ; d) 2 - √5 < 0
* Lời giải bài 1 trang 9 sgk đại số 10:
a) 3 + 2 = 7 là mệnh đề và là mệnh đề sai: Vì 3 + 2 = 5 ≠ 7
b) 4 + x = 3 là mệnh đề chứa biến: Vì với mỗi giá trị của x ta được một mệnh đề.
Ví dụ : với x = 1 ta có mệnh đề « 4 + 1 = 3 ».
với x = –1 ta có mệnh đề « 4 + (–1) = 3 ».
với x = 0 ta có mệnh đề 4 + 0 = 3.
c) x + y > 1 là mệnh đề chứa biến: Vì với mỗi cặp giá trị của x, y ta được một mệnh đề.
Ví dụ : x = 0 ; y = 1 ta có mệnh đề « 0 + 1 > 1 »
x = 1 ; y = 3 ta có mệnh đề « 1 + 3 > 1 ».
d) 2 – √5 < 0 là mệnh đề và là mệnh đề đúng: Vì 2 = √4 và √4 < √5.
Bài 2 trang 9 sgk đại số 10: Xét tính đúng sai của mỗi mệnh đề sau và phát biểu mệnh đề phủ định của nó:
a) 1794 chia hết cho 3 ;
b) √2 là một số hữu tỉ
c) π < 3, 15 ; d) |-125| ≤ 0;
* Lời giải bài 2 trang 9 sgk đại số 10:
a) Mệnh đề "1794 chia hết cho 3" Đúng vì 1794:3 = 598
- Mệnh đề phủ định: "1794 không chia hết cho 3"
b) Mệnh đề "√2 là số hữu tỉ’" Sai vì √2 là số vô tỉ
- Mệnh đề phủ định: "√2 không phải là một số hữu tỉ"
c) Mệnh đề π < 3, 15 Đúng vì π = 3,141592654...
- Mệnh đề phủ định: "π ≥ 3, 15"
d) Mệnh đề "|–125| ≤ 0" sai vì |–125| = 125 > 0
- Mệnh đề phủ định: "|–125| > 0"
Bài 3 trang 9 SGK Đại số 10: Cho các mệnh đề kéo theo:
Nếu a và b cùng chia hết cho c thì a + b chia hết cho c (a, b, c là những số nguyên).
Các số nguyên tố có tận cùng bằng 0 đều chia hết cho 5.
Một tam giác cân có hai đường trung tuyến bằng nhau.
Hai tam giác bằng nhau có diện tích bằng nhau.
a) Hãy phát biểu mệnh đề đảo của mỗi mệnh đề trên.
b) Hãy phát biểu mỗi mệnh đề trên, bằng cách sử dụng khái niệm "điều kiện đủ".
c) Phát biểu mỗi mệnh đề trên, bằng cách sử dụng khái niệm "điều kiện cần".
* Lời giải Bài 3 trang 9 SGK Đại số 10:
| Mệnh đề | Mệnh đề đảo | Phát biểu bằng khái niệm "điều kiện đủ" | Phát biểu bằng khái niệm "điều kiện cần" |
| Nếu a và b cùng chia hết cho c thì a+b chia hết cho c. | Nếu a+b chia hết cho c thì cả a và b đều chia hết cho c. | a và b chia hết cho c là điều kiện đủ để a+b chia hết cho c. | a+b chia hết cho c là điều kiện cần để a và b chia hết cho c. |
| Các số nguyên có tận cùng bằng 0 đều chia hết cho 5. | Các số nguyên chia hết cho 5 thì có tận cùng bằng 0. | Một số nguyên tận cùng bằng 0 là điều kiện đủ để số đó chia hết cho 5. | Các số nguyên chia hết cho 5 là điều kiện cần để số đó có tận cùng bằng 0. |
| Tam giác cân có hai đường trung tuyến bằng nhau | Tam giác có hai đường trung tuyến bằng nhau là tam giác cân. | Tam giác cân là điều kiện đủ để tam giác đó có hai đường trung tuyến bằng nhau. | Hai trung tuyến của một tam giác bằng nhau là điều kiện cần để tam giác đó cân. |
| Hai tam giác bằng nhau có diện tích bằng nhau | Hai tam giác có diện tích bằng nhau là hai tam giác bằng nhau. | Hai tam giác bằng nhau là điều kiện đủ để hai tam giác đó có diện tích bằng nhau. | Hai tam giác có diện tích bằng nhau là điều kiện cần để hai tam giác đó bằng nhau. |
Bài 4 trang 9 SGK Đại số 10: Phát biểu mỗi mệnh đề sau, bằng cách sử dụng khái niệm "điều kiện cần và đủ".
a) Một số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và ngược lại.
b) Một hình bình hành có các đường chéo vuông góc là một hình thoi và ngược lại.
c) Phương trình bậc hai có hai nghiệm phân biệt khi và chỉ khi biệt thức của nó dương.
* Lời giải bài 4 trang 9 SGK Đại số 10
a) Điều kiện cần và đủ để một số chia hết cho 9 là tổng các chữ số của nó chia hết cho 9.
b) Một hình bình hành có các đường chéo vuông góc là điều kiện cần và đủ để nó là một hình thoi.
c) Để phương trình bậc hai có hai nghiệm phân biệt, điều kiện cần và đủ là biệt thức của nó dương.
Bài 5 trang 10 SGK Đại số 10: Dùng kí hiệu ∀, ∃ để viết các mệnh đề sau:
a) Mọi số nhân với 1 đều bằng chính nó.
b) Có một số cộng với chính nó bằng 0.
c) Mọi số cộng với số đối của nó đều bằng 0.
* Lời giải bài 5 trang 10 SGK Đại số 10:
a) ∀ x ∈ R: x.1 = x
b) ∃ a ∈ R: a + a = 0
c) ∀ x ∈ R: x + (-x) = 0
Bài 6 trang 10 SGK Đại số 10: Phát biểu thành lời mỗi mệnh đề sau và xét tính đúng sai của nó.
a) ∀ x∈R : x2 > 0 ;
b) ∃ n∈N : n2 = n
c) ∀ n∈N; n ≤ 2n
d) ∃ x∈R : x < 1/x.
* Lời giải bài 6 trang 10 SGK Đại số 10:
a) Bình phương của mọi số thực đều dương.
- Mệnh đề này sai vì khi x = 0 thì x2 = 0.
- Sửa cho đúng: ∀x∈R : x2 ≥ 0.
b) Tồn tại số tự nhiên mà bình phương của nó bằng chính nó.
- Mệnh đề này đúng. Vì có: n = 0; n = 1.
c) Mọi số tự nhiên đều nhỏ hơn hoặc bằng hai lần của nó.
- Mệnh đề này đúng.
d) Tồn tại số thực nhỏ hơn nghịch đảo của chính nó.
- Mệnh đề này đúng. Vì có: 0,5 < 1/0,5.
Bài 7 trang 10 SGK Đại số 10: Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó:
a) ∀ n ∈ N: n chia hết cho n ;
b) ∃ x ∈ Q : x2 = 2
c) ∀ x ∈ R : x < x + 1;
d) ∃ x ∈ R: 3x = x2 + 1
* Lời giải bài 7 trang 10 SGK Đại số 10:
a) A: "∀ n ∈ N: n chia hết cho n"
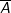 : "∃ n ∈ N: n không chia hết cho n".
: "∃ n ∈ N: n không chia hết cho n".
⇒ 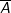 đúng vì với n = 0 thì n không chia hết cho n.
đúng vì với n = 0 thì n không chia hết cho n.
b) B: "∃ x ∈ Q: x2 = 2".
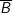 : "∀ x ∈ Q: x2 ≠ 2".
: "∀ x ∈ Q: x2 ≠ 2". 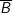 : Đúng
: Đúng
c) C: "∀ x ∈ R : x < x + 1".
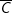 : “∃ x ∈ R: x ≥ x + 1”.
: “∃ x ∈ R: x ≥ x + 1”.
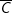 : Sai vì x + 1 luôn lớn hơn x.
: Sai vì x + 1 luôn lớn hơn x.
d) D: "∃ x ∈ R: 3x = x2 + 1".
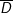 : "∀ x ∈ R: 3x ≠ x2 + 1".
: "∀ x ∈ R: 3x ≠ x2 + 1". 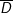 Sai.
Sai.
Từ khóa » Các Bài Toán Về Mệnh đề Lớp 10
-
Bài Tập Mệnh đề Lớp 10 Chọn Lọc, Có Lời Giải
-
Bài Tập Mệnh đề Toán Học Lớp 10
-
Các Dạng Bài Tập Toán Về Mệnh đề Và Tập Hợp - Lớp 10
-
Các Dạng Bài Tập Mệnh đề - Tập Hợp
-
Các Dạng Bài Tập Mệnh đề, Tập Hợp Chọn Lọc Có Lời Giải - Toán Lớp 10
-
Các Bài Toán Liên Quan đến Mệnh đề Phủ định Và Cách Giải - Haylamdo
-
Các Dạng Bài Tập Về Mệnh đề Toán Lớp 10 - Deha Law
-
Các Bài Toán Về Mệnh đề - Lớp 10 - Thầy Nguyễn Mạnh Cường
-
Lý Thuyết Và Bài Tập Mệnh đề - Toán Lớp 10 - Trường Quốc Học
-
Các Dạng Bài Tập Mệnh đề - Tập Hợp | Toán Lớp 10
-
Bài Tập Chuyên đề Mệnh đề -tập Hợp Lớp 10 Chọn Lọc
-
Tổng Hợp Các Dạng Toán Về Mệnh đề Và Các Phép Toán Tập Hợp
-
Bài Tập Tự Luận Môn Toán Lớp 10 Về Mệnh đề
-
Lý Thuyết Về Mệnh đề | SGK Toán Lớp 10