Cách Tìm Cực Trị Của Hàm Số Bậc 3 (tìm Cực đại, Cực Tiểu ... - HayHocHoi
Có thể bạn quan tâm
Vậy cách tìm cực trị của hàm số bậc 3 (tìm cực đại, cực tiểu của hàm số bậc 3) như thế nào? Chúng ta hãy cùng tìm hiểu qua bài viết dưới đây. Đồng thời, qua bài viết này các em dễ dàng trả lời được các câu hỏi như: Hàm số bậc 3 có bao nhiêu cực trị? Điều kiện để hàm số bậc 3 có cực trị là gì? Hàm số bậc 3 có 2 cực trị khi nào?...
° Cách tìm cực trị của hàm số bậc 3 (tìm cực đại, cực tiểu của hàm số bậc 3)
* Xét hàm số bậc hai: y = f(x) = ax3 + bx3 + cx + d (a≠0)
Cách 1:
- Bước 1: TXĐ: D = R
- Bước 2: Tính y' = 3ax2 + 2bx + c, cho y'=0 (hoặc y' không xác định)
- Bước 3: Lập bảng biến thiên
- Bước 4: Từ bảng biến thiên suy ra các điểm cực trị
* Lưu ý: Khi y'=0 ta tính Δ' = b2 – 3ac, nếu:
Δ' ≤ 0 : y’ không đổi dấu ⇒ hàm số không có cực trị
Δ' > 0 : y’ đổi dấu 2 lần ⇒ hàm số có hai cực trị (1 cực đại và 1 cực tiểu)
Cách 2:
- Bước 1: Tìm tập xác định
- Bước 2: Tính f'(x), giải phương trình f'(x)=0 và ký hiệu xi (i=1;2;...) là nghiệm
- Bước 3: Tính f''(x) và f''(xi)
- Bước 4: Dựa vào dấu của f''(xi) suy ra tính chất cực trị của điểm xi.
* Ví dụ 1: Tìm điểm cực trị của hàm số bậc 3 sau: f(x) = x3 - 3x
* Lời giải:
Cách 1:
- TXĐ: D = R.
Ta có: f(x) = x3 – 3x
Khi đó: f’(x) = (x3 – 3x)' = 3x2 – 3
- Cho f’(x) = 0 ⇔ 3x2 – 3 = 0
⇔ x2 – 1 = 0 ⇔ x = -1 hoặc x = 1
- Ta có bảng biến thiên như sau: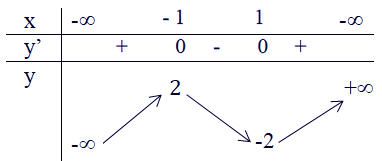
- Từ bảng biến thiên, ta thấy:
Hàm số đạt cực đại tại x = -1 và giá trị cực đại là 2 điểm cực đại là (-1; 2).
Hàm số đạt cực tiểu tại x = 1 và giá trị cực tiểu là -2 điểm cự tiểu là (1; -2)
Cách 2:
- TXĐ: D = R
Ta có: f(x) = x3 – 3x
Khi đó: f’(x) = (x3 – 3x)' = 3x2 – 3
- Cho f’(x) = 0 ⇔ 3x2 – 3 = 0
⇔ x2 – 1 = 0 ⇔ x1 = -1 và x2 = 1
- Lại có: f''(x) = (3x2 - 3)' = 6x;
Nên có:
f''(x1) = f''(-1) = -6<0 ⇒ x1 là điểm cực đại
f''(x2) = f''(1) = 6>0 ⇒ x2 là điểm cực tiểu
* Ví dụ 2: Hãy tìm các điểm cực trị của các hàm số bậc 3 sau: y = 2x3 + 3x2 - 36x - 10;
* Lời giải:
Cách 1:
- TXĐ: D = R
- Ta có: y' = 6x2 + 6x - 36
y' = 0 ⇔ 6x2 + 6x - 36 = 0
⇔ x = 2 hoặc x = -3
- Bảng biến thiên:
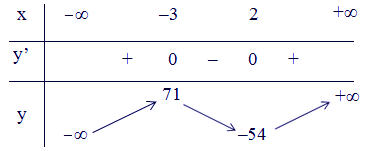
- Từ bảng biến thiên ta thấy:
Hàm số đạt cực đại tại x = -3 ; yCĐ = 71
Hàm số đạt cực tiểu tại x = 2; yCT = -54.
Cách 2:
- TXĐ: D = R
- Ta có: y' = 6x2 + 6x - 36
y' = 0 ⇔ 6x2 + 6x - 36 = 0
⇔ x1 = -3 và x2 = 2
- Lại có: y'' = 12x + 6, nên có:
y''(x1) = y''(-3) = 12.(-3) + 6 = -30<0 ⇒ x1 = -3 là điểm cực đại, yCĐ = 71.
y''(x2) = y''(2) = 12.2 + 6 = 30>0 ⇒ x2 = 2 là điểm cực tiểu, yCT = -54.
Từ khóa » Tính Chất Cực Trị Hàm Bậc 3
-
Chuyên đề Cực Trị Hàm Số Bậc 3 Và Công Thức Tính Nhanh Cực Trị
-
Cực Trị Hàm Số Bậc 3 ? Công Thức, điều Kiện, Bài Tập để Tìm Cực Trị ...
-
Cực Trị Hàm Số Bậc 3 (có Lời Giải Chi Tiết)
-
Công Thức Tính Nhanh Cực Trị Hàm Bậc 3 - TopLoigiai
-
I. CỰC TRỊ CỦA HÀM SỐ BẬC BA LÀ GÌ
-
Ứng Dụng Đồ Thị Hàm Số Bậc 3 Vào Giải Toán - Kiến Guru
-
Công Thức Giải Nhanh Cực Trị Hàm Bậc 3 Của Hàm Số - Bierelarue
-
Chuyên đề Cực Trị Của Hàm Số Bậc 3 Phần 1 Luyện Thi đại Học-đặng ...
-
LÝ THUYẾT CỰC TRỊ HÀM SỐ BẬC 3 | PDF - Scribd
-
Công Thức Giải Nhanh Bài Toán Cực Trị Của Hàm Số Trùng Phương
-
Cực Trị Hàm Số Bậc 3 - Cổng Thông Tin Đại Học, Cao Đẳng Lớn ...
-
Cách Tìm Cực Trị Của Hàm Bậc Ba Cực Hay, Có Lời Giải - Toán Lớp 12
-
Tìm điều Kiện để Hàm Số Bậc Ba đạt Cực Trị (hoặc đạt ... - Tự Học 365
-
Tổng Hợp Lý Thuyết Tìm điều Kiện để Hàm Số Bậc Ba đạt Cực Trị (hoặc ...