Cực Trị Hàm Số Bậc 3 ? Công Thức, điều Kiện, Bài Tập để Tìm Cực Trị ...

Home » Toán Học » Cực trị hàm số bậc 3 ? Công thức, điều kiện, bài tập để tìm cực trị hàm bậc 3 ? Toán Học Cực trị hàm số bậc 3 ? Công thức, điều kiện, bài tập để tìm cực trị hàm bậc 3 ? admin.ta 17 Tháng Chín, 2021 1023 Views 0 SaveSavedRemoved 0

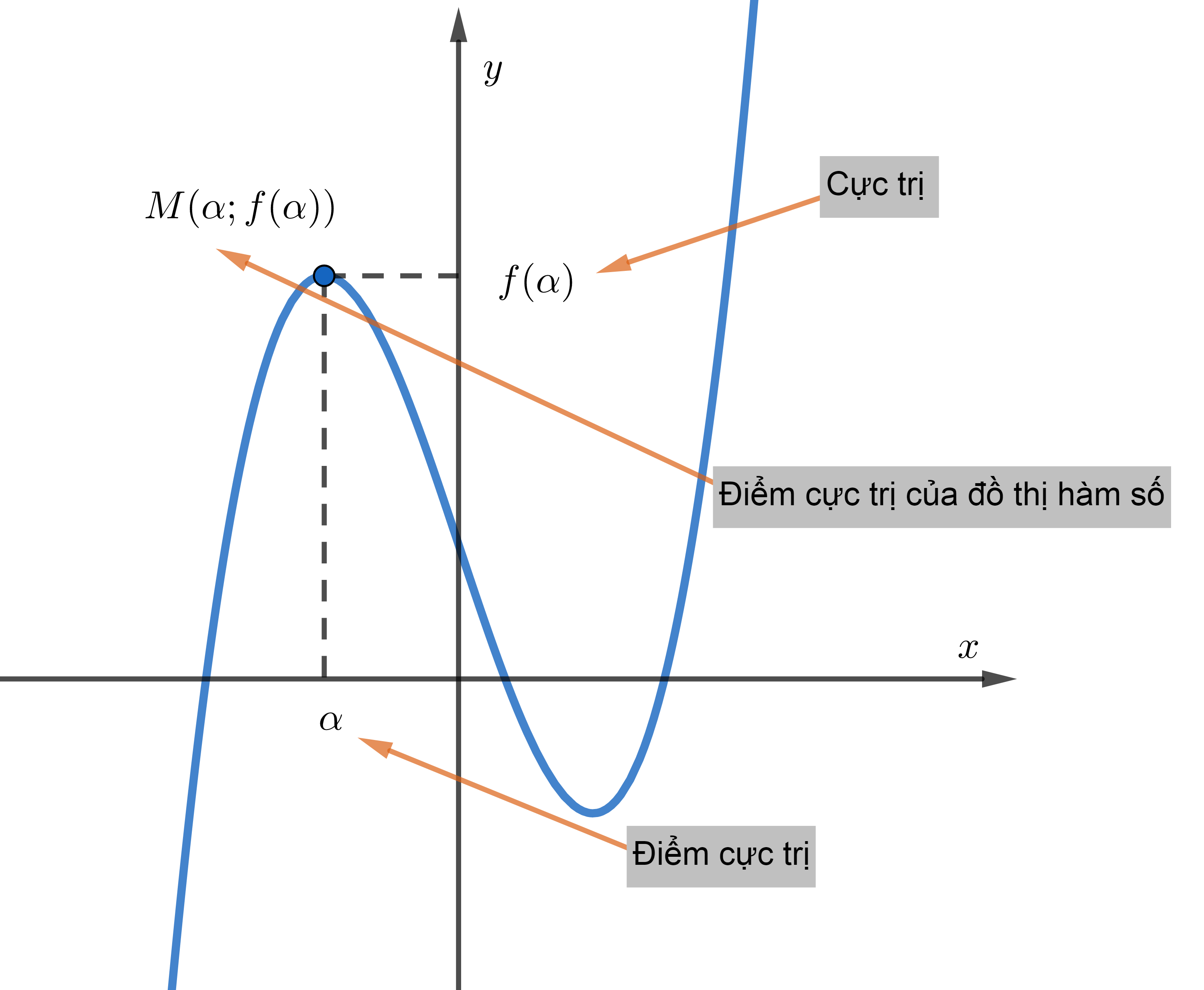
Cực trị hàm số bậc 3 cũng là một nội dung khá quan trọng trong hệ thống kiến thức toán học chuẩn bị cho kỳ thi quan trọng. Hãy cùng chúng tôi theo dõi những nội dung dưới bài viết này để hiểu hơn về dạng toán này nhé !

Tham khảo bài viết khác: 

• Cực trị hàm số bậc 4 trùng phương
• Diện tích tam giác vuông cân khi biết cạnh huyền hoặc biết 1 cạnh

     Cực trị hàm số bậc 3 là gì ?

Tóm tắt nội dung

• 1      Cực trị hàm số bậc 3 là gì ?
• 2     Hướng dẫn phương pháp cách tìm cực trị của hàm số bậc 3
• 3     Một số điều kiện tìm cực trị của hàm số bậc 3
• 4      Bài tập tìm cực trị của hàm số bậc 3

Cho hàm số bậc 3 y = f(x)= ax^3 + bx^2 + cx + d

+) Đạo hàm y′ = f′(x)=3ax^2 + 2bx + c

+) Hàm số f(x) có cực trị ⇔f(x) có cực đại và cực tiểu

• ⇔ f′(x)=0 có hai nghiệm phân biệt ⇔ Δ‘ = b^2 − 3ac > 0
• ⇔ Hàm số f(x) không có cực trị ⇔ Δ‘= b^2 − 3ac ≤ 0

    Hướng dẫn phương pháp cách tìm cực trị của hàm số bậc 3

– Bước 1:

+) Tính đạo hàm của hàm số y’ = 3ax^2 + 2bx + c

+) Cho y’ = 0 ⇔ 3ax^2 + 2bx + c = 0 (1)

+) Để hàm số đã cho có cực đại và cực tiểu ⇔ y’ = 0 phải có hai nghiệm phân biệt ⇔ (1) phải có hai nghiệm phân biệt

+) Ta có a ≠ 0 và ∆ (∆’) ≠ 0 ⇔ Giá trị tham số cần tìm thuộc 1 miền D nào đó (*)

– Bước 2:

+) Từ điều kiện bài toán cho trước ta có 1 phương trình hoặc 1 bất phương trình theo tham số cần tìm

+) Giải phương trình này ta sẽ tìm được tham số rồi sau đó đối chiếu với điều kiện (*) của tham số và kết luận.

Tham khảo thêm Tuổi Mão nên mua xe màu gì ? Màu xe thu hút tài lộc, may mắn

    Một số điều kiện tìm cực trị của hàm số bậc 3

– Để hàm số y = f(x) đã cho có 2 cực trị <=> a ≠ 0 và ∆y′  (∆’) > 0

– Để hàm số y = f(x) đã cho có 2 cực trị nằm về hai phía đối nhau của trục hoành <=> yCD . yCT < 0

– Để hàm số y = f(x) đã cho có 2 cực trị nằm về hai phía đối nhau của trục tung <=> yCD . yCT < 0

– Để hàm số y = f(x) đã cho có 2 cực trị cùng nằm phía trên của trục hoành <=>

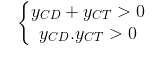
– Để hàm số y = f(x) đã cho có 2 cực trị cùng nằm phía dưới của trục hoành <=>

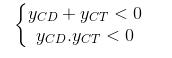
– Để hàm số y = f(x) đã cho có cực trị nằm tiếp xúc với trục hoành <=> yCD . yCT = 0

– Đồ thị hàm số có 2 điểm cực trị khác nằm phía đối với đường thẳng d có dạng: Ax + By + C = 0

Gọi M1 (x1; y1) và M2( x2; y2) là điểm cực đại và điểm cực tiểu của hàm số y = f(x)

Ta có t1 và t2 là giá trị của các điểm cực trị M1, M2 khi ta thay vào đường thẳng d.

t1 = Ax1 + By1 + C t2 = Ax2 + By2+ C

==> có 2 nghiệm phân biệt x1, x2

     Bài tập tìm cực trị của hàm số bậc 3

Ví dụ 1: Tìm m đề hàm số f(x) = y = 2x^3 + 3(m−1)x^2 + 6(m−2)x – 1 có hai điểm cực trị

– Hướng dẫn giải:

Xét y = 2x^3 + 3(m−1)x^2 + 6(m−2)x – 1 có tập xác định D=R

Ta có :

y′ = 6x^2 + 6(m−1)x + 6(m−2)

Để hàm số có hai cực trị thì y′=0 có hai nghiệm phân biệt

⇔x^2 + (m−1)x + (m−2) = 0 có hai nghiệm phân biệt

⇔Δ = (m−1)^2 − 4(m−2) > 0

⇔ m^2 − 6m + 9 = (m−3)^2 > 0

⇔ m≠3

Cám ơn bạn đã theo dõi bài viết này của chúng tôi, hy vọng với những thông tin mà chúng tôi chia sẻ đến bạn sẽ giúp bạn giải quyết được những bài toán của mình nhé !

Người xem: 1.445