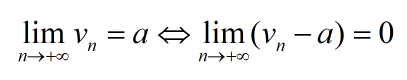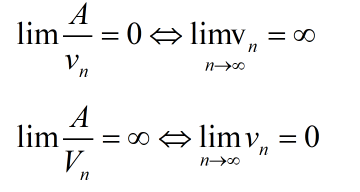Cách Tính Lim Bằng Tay Của Hàm Số, Bằng Phương Pháp Thủ Công ...

Home » Toán Học » Cách tính lim bằng tay của hàm số, bằng phương pháp thủ công đơn giản nhất Toán Học Cách tính lim bằng tay của hàm số, bằng phương pháp thủ công đơn giản nhất admin.ta 20 Tháng Chín, 2021 82 Views 0 SaveSavedRemoved 0

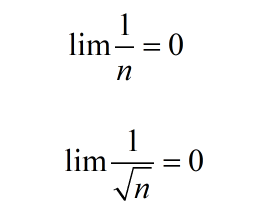
Cách tính lim bằng tay của hàm số trong bài viết này của chúng tôi sẽ giúp bạn nhanh chóng giải được những bài toán giới hạn tính lim bằng phương pháp thủ công

Hãy đọc kỹ bài viết này và bỏ túi những cách giải lim nhanh chóng, đơn giản trong bài viết này của chúng tôi nhé !

Tham khảo bài viết khác:

• Giới hạn hàm số lượng giác
• Giới hạn của hàm số

     Cách giải Lim bằng tay đơn giản

Tóm tắt nội dung

• 1      Cách giải Lim bằng tay đơn giản
  • 1.1   1. Dạng 0/0 đối với giới hạn tại một điểm
  • 1.2     2.
  • 1.3      3. Dạng ∞; – ∞  : Ta sẽ nhân lượng liên hợp
  • 1.4     4. Dạng 0.∞: Ta biến đổi về dạng ∞/∞ hoặc 0/0
• 2        Một số cách tính Lim thủ công khác
  • 2.1   1.  Sử dụng định nghĩa tìm giới hạn 0 của dãy số
  • 2.2   2. Tìm giới hạn của dãy số bằng công thức
  • 2.3    3. Sử dụng định nghĩa tìm giới hạn hữu hạn
  • 2.4    4. Sử dụng các giới hạn đặc biệt cùng với định lý để giải quyết các bài toán tìm giới hạn dãy số

  1. Dạng 0/0 đối với giới hạn tại một điểm

Ví dụ 1: 

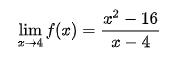
+) Bước 1: Ta thế 4 vào phương trình f(x) thì sẽ được dạng 0/0 nên khẳng định đây là dạng 0/0

+) Bước 2: Biến đổi:

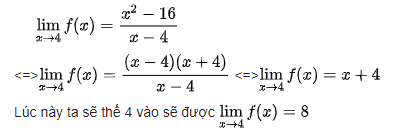
    2.

+) Ví dụ 1: Dạng đã biến đổi

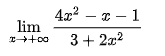
Lúc này ta thấy số mũ lớn nhất của tử và mẫu là x^2, vì vậy ta sẽ chia cả tử và mẫu cho x^2

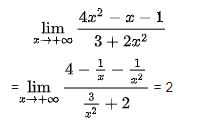
 +) Ví dụ 2: Dạng chưa biến đổi

     3. Dạng ∞; – ∞  : Ta sẽ nhân lượng liên hợp

Ví dụ 1: 

Tham khảo thêm Tuổi Mão nên mua xe màu gì ? Màu xe thu hút tài lộc, may mắn

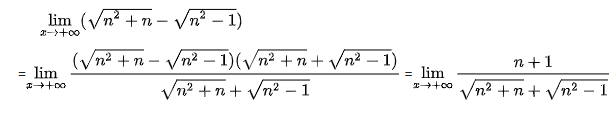
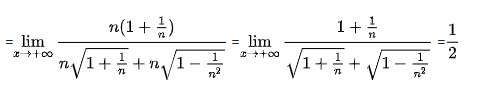
    4. Dạng 0.∞: Ta biến đổi về dạng ∞/∞ hoặc 0/0

– Ví dụ minh họa:

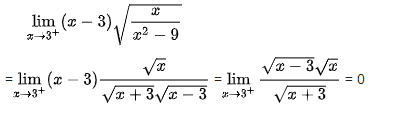
       Một số cách tính Lim thủ công khác

  1.  Sử dụng định nghĩa tìm giới hạn 0 của dãy số

  2. Tìm giới hạn của dãy số bằng công thức

– Một số công thức ta thường gặp khi tính giới hạn hàm số như sau:

==> Công thức trên có thể biến tấu thành các dạng khác tuy nhiên về bản chất thì không thay đổi.

   3. Sử dụng định nghĩa tìm giới hạn hữu hạn

   4. Sử dụng các giới hạn đặc biệt cùng với định lý để giải quyết các bài toán tìm giới hạn dãy số

+) Ta thường sử dụng các dạng giới hạn:

+) Nếu biểu thức có dạng phân thức tử số và mẫu số chứa lũy thừa của n thì ta tiến hành chia cả tử và mẫu cho n^k với k là mũ cao nhất ở bậc mẫu.

+) Nếu biểu thức chứa căn thức cần nhân một lượng liên hợp để đưa về dạng cơ bản thì ta có một số lượng liên hợp cần thiết

Cám ơn bạn đã theo dõi bài viết này của chúng tôi, chúc bạn thành công và may mắn !

Người xem: 590