Cách Viết Phương Trình Tiếp Tuyến TẠI 1 điểm Của đường Tròn

KhoiA.Vn sẽ giới thiệu với các em cách viết phương trình tiếp tuyến tại 1 điểm của đường tròn một cách gắn gọn, đầy đủ và dễ hiểu để các em dễ dàng vận dụng cho các bài tập tương tự.

I. Cách viết phương trình tiếp tuyến TẠI 1 điểm của đường tròn

Giả sử đường tròn (C) có tâm I(a; b); bán kính R và điểm M(x0; y0):

Lập phương trình tiếp tuyến (d) của (C) tại điểm M: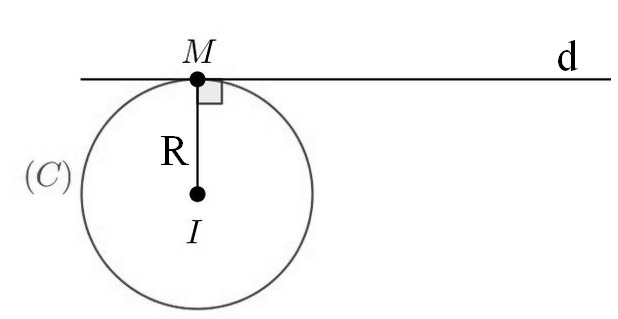Để viết phương trình tiếp tuyến tại 1 điểm của đường tròn ta thực hiện như sau:

Do (d) là tiếp tuyến của đường tròn tại M nên d vuông góc IM

⇒ Đường thẳng (d) :  

⇒ Phương trình đường thẳng (d) có dạng:

 (x0 - a)(x - x0) + (y0 - b)(y - y0) = 0

II. Bài tập viết phương trình tiếp tuyến TẠI 1 điểm của đường tròn

* Bài tập 1: Cho đường tròn (C): (x - 3)2 + (y - 1)2 = 10.

Viết phương trình tiếp tuyến của (C) tại điểm M(2; 4).

> Lời giải:

- Đường tròn (C) có tâm I(3; 1). Gọi (d) là tiếp tuyến của đường tròn (C) tại điểm M(2; 4) (M ∈ (C)); khi đó (d) và IM vuông góc với nhau, , hay (d) có véctơ pháp tuyến là :

 là vectơ pháp tuyến của d.

Vậy phương trình tiếp tuyến (d) có dạng: (-1).(x - xM) + 3(y - yM) = 0

⇔ (-1).(x - 2) + 3(y - 4) = 0

⇔ -x + 3y - 10 = 0

⇔ x - 3y + 10 = 0.

Vậy phương trình tiếp tuyến (d) của (C) tại điểm M(2;4) là: x - 3y + 10 = 0.

* Bài tập 2: Viết Phương trình tiếp tuyến d của đường tròn (C):

(x - 2)2 + (y - 2)2 = 25 tại điểm M(-2; 5).

> Lời giải:

- Đường tròn (C) có tâm I(2; 2) bán kính R = 5.

-  Do đường thẳng (d) tiếp xúc với đường tròn tại điểm M(-2; 5) nên hai đường thẳng (d) và IM vuông góc với nhau, hay (d) có véctơ pháp tuyến là 

 

Vậy phương trình tiếp tuyến (d) có dạng: (-4).(x - xM ) + 3(y - yM) = 0

⇔ (-4).(x + 2) + 3(y - 5) = 0

⇔ -4x + 3y - 23 = 0

⇔ 4x - 3y + 23 = 0.

Vậy phương trình tiếp tuyến (d) của (C) tại điểm M(-2;5) là: x - 3y + 10 = 0.