Cho A3 B3=2 . Chứng Minh Rằng A B - Hoc24
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
Trịnh Xuân Minh 3 tháng 4 2016 lúc 21:55 Cho a3+b3=2 . Chứng minh rằng a+b<=2
Lớp 8 Toán Những câu hỏi liên quan
- chuche
-
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|
Câu 9.
a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
Câu 10. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Câu 11. Tìm các giá trị của x sao cho:
a) |2x – 3| = |1 – x|
b) x2 – 4x ≤ 5
c) 2x(2x – 1) ≤ 2x – 1.
Câu 12. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 13. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Xem chi tiết Lớp 1 Toán 8 0
Gửi Hủy 
Nguyễn Hoàng Minh 
31 tháng 10 2021 lúc 18:12 Câu 9:
\(a,\left(a+1\right)^2\ge4a\\ \Leftrightarrow a^2+2a+1\ge4a\\ \Leftrightarrow a^2-2a+1\ge0\\ \Leftrightarrow\left(a-1\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=1\)
\(b,\) Áp dụng BĐT cosi: \(\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge2\sqrt{a}\cdot2\sqrt{b}\cdot2\sqrt{c}=8\sqrt{abc}=8\)
Dấu \("="\Leftrightarrow a=b=c=1\)
Câu 10:
\(a,\left(a+b\right)^2\le2\left(a^2+b^2\right)\\ \Leftrightarrow a^2+2ab+b^2\le2a^2+2b^2\\ \Leftrightarrow a^2-2ab+b^2\ge0\\ \Leftrightarrow\left(a-b\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b\)
\(b,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\le3a^2+3b^2+3c^2\\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
Câu 13:
\(M=\left(a^2+ab+\dfrac{1}{4}b^2\right)-3\left(a+\dfrac{1}{2}b\right)+\dfrac{3}{4}b^2-\dfrac{3}{2}b+2021\\ M=\left[\left(a+\dfrac{1}{2}b\right)^2-2\cdot\dfrac{3}{2}\left(a+\dfrac{1}{2}b\right)+\dfrac{9}{4}\right]+\dfrac{3}{4}\left(b^2-2b+1\right)+2018\\ M=\left(a+\dfrac{1}{2}b-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\left(b-1\right)^2+2018\ge2018\\ M_{min}=2018\Leftrightarrow\left\{{}\begin{matrix}a+\dfrac{1}{2}b=\dfrac{3}{2}\\b=1\end{matrix}\right.\Leftrightarrow a=b=1\)
Đúng 3 Bình luận (0) Gửi Hủy 
Akai Haruma Giáo viên 31 tháng 10 2021 lúc 20:30 Câu 6:
$2=(a+b)(a^2-ab+b^2)>0$
$\Rightarrow a+b>0$
$4(a^3+b^3)-N^3=4(a^3+b^3)-(a+b)^3$
$=3(a^3+b^3)-3ab(a+b)=(a+b)(a-b)^2\geq 0$$\Rightarrow N^3\leq 4(a^3+b^3)=8$
$\Rightarrow N\leq 2$
Vậy $N_{\max}=2$
Đúng 5 Bình luận (0) Gửi Hủy Akai Haruma Giáo viên 31 tháng 10 2021 lúc 20:32 Câu 7:
BĐT $\Leftrightarrow a^3+b^3\geq ab(a+b)$
$\Leftrightarrow a^3+b^3-ab(a+b)\geq 0$
$\Leftrightarrow (a-b)^2(a+b)\geq 0$ (luôn đúng với mọi $a,b,c>0$)
Vậy ta có đpcm
Dấu "=" xảy ra khi $a=b>0$, $c$ dương bất kỳ.
Đúng 5 Bình luận (0) Gửi Hủy Xem thêm câu trả lời 
- Phạm Thanh Lâm
Cho a, b, c > 0 . Chứng minh rằng a3 +b3 +c3 >=3abc.
Xem chi tiết Lớp 8 Toán 4 0 Gửi Hủy 
Nguyễn Lê Phước Thịnh CTV 
3 tháng 1 2022 lúc 20:58 \(\Leftrightarrow a^3+b^3+c^3-3abc>=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc>=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)>=0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac>=0\)(vì a+b+c>0)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2>=0\)(luôn đúng)
Đúng 1 Bình luận (0) Gửi Hủy Nguyễn Hoàng Minh 3 tháng 1 2022 lúc 20:58 \(a^3+b^3+c^3\ge3abc\\ \Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc\ge0\\ \Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\ge0\\ \Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\ge0\)
Vì \(a,b,c>0\Leftrightarrow a+b+c>0\)
Lại có \(a^2+b^2+c^2-ab-bc-ca=\dfrac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)
Nhân vế theo vế ta được đpcm
Dấu \("="\Leftrightarrow a=b=c\)
Đúng 0 Bình luận (0) Gửi Hủy 
duong thu 3 tháng 1 2022 lúc 21:00 ⇔a3+b3+c3−3abc>=0⇔a3+b3+c3−3abc>=0
⇔(a+b)3+c3−3ab(a+b)−3abc>=0⇔(a+b)3+c3−3ab(a+b)−3abc>=0
⇔(a+b+c)(a2+b2+c2−ab−bc−ac)>=0⇔(a+b+c)(a2+b2+c2−ab−bc−ac)>=0
⇔2a2+2b2+2c2−2ab−2bc−2ac>=0⇔2a2+2b2+2c2−2ab−2bc−2ac>=0(vì a+b+c>0)
⇔(a−b)2+(a−c)2+(b−c)2>=0⇔(a−b)2+(a−c)2+(b−c)2>=0(luôn đúng)
Đúng 1 Bình luận (0) Gửi Hủy Xem thêm câu trả lời 
- Pham Trong Bach
Cho a + b + c = 0. Chứng minh rằng a 3 + b 3 + c 3 = 3abc.
Xem chi tiết Lớp 8 Toán 2 0 Gửi Hủy 
Cao Minh Tâm 
22 tháng 5 2019 lúc 13:47 
Gửi Hủy 
Võ Tài Hưng 21 tháng 12 2021 lúc 15:05 a3+b3+c3= (a+b)3-3ab(a+b)+c3Thay a+b=-c vào, ta được: a3 + b3 +c3 = (-c)3 -3ab(-c) +c3 = 3abc (đpcm)
Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy 
- Nguyen hoan
Xét a,b là các số thực thỏa mãn:
1. a3 + a = 3 và b3 + b = 3. Chứng minh rằng a=b.
2. a3+ 3a2+ 4a - 2 =0 và b3- 3b2 + 4b - 7 =0. Tính a + b ?
10:59 Xem chi tiết Lớp 7 Toán Câu hỏi của OLM 1 0 Gửi Hủy 
ngô thái dương 24 tháng 10 2023 lúc 16:50 1. b3+b= 3
(b3+b)=3
b.(3+1)=3
b. 4= 3
b=\(\dfrac{3}{4}\)
a3+a= 3 b3
(a3+a)=3
a.(3+1)=3
a. 4= 3
a=\(\dfrac{3}{4}\)
2
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Chứng minh rằng: a3 – b3 = (a – b)3 + 3ab(a – b)
Xem chi tiết Lớp 8 Toán 1 0 Gửi Hủy Cao Minh Tâm 8 tháng 3 2017 lúc 3:50 Biến đổi vế phải ta được:
(a – b)3 + 3ab(a – b)
= a3 – 3a2b + 3ab2 – b3 + 3a2b – 3ab2
= a3 – b3
Vậy a3 – b3 = (a – b)3 + 3ab(a – b)
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Chứng minh rằng: a3 + b3 = (a + b)3 – 3ab(a + b)
Xem chi tiết Lớp 8 Toán 1 0 Gửi Hủy Cao Minh Tâm 19 tháng 7 2018 lúc 3:11 Biến đổi vế phải ta được:
(a + b)3 – 3ab(a + b)
= a3 + 3a2b + 3ab2 + b3 – 3a2b – 3ab2
= a3 + b3
Vậy a3 + b3 = (a + b)3 – 3ab(a + b)
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Chứng minh rằng: a 3 + b 3 = (a + b)[ a - b 2 + ab]
Xem chi tiết Lớp 8 Toán 1 0 Gửi Hủy Cao Minh Tâm 8 tháng 2 2019 lúc 16:49 Biến đổi vế trái ta có:
VT = a 3 + b 3 =(a+b)( a 2 -ab+ b 2 )
=(a+b)( a 2 -2ab+ b 2 +ab)
=(a + b)[ a - b 2 + ab] = VP
Vế phải bằng vế trái nên đẳng thức được chứng minh.
Đúng 0 Bình luận (0) Gửi Hủy 
- NGUYỄN ĐÌNH ANH
Cho a, b là các số thực dương mà a3 +b3 = a−b. Chứng minh rằng a2 +4b2 < 1.
Xem chi tiết Lớp 8 Toán 0 0 Gửi Hủy 
- Phạm Mỹ Hạnh
-
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].
Câu 32. Tìm giá trị lớn nhất của biểu thức: 
Câu 33. Tìm giá trị nhỏ nhất của: 
với x, y, z > 0.
Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:
a) ab và a/b là số vô tỉ.
b) a + b và a/b là số hữu tỉ (a + b ≠ 0)
c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)
Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 38. Cho a, b, c, d > 0. Chứng minh:
Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1
Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa:
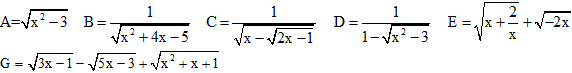Mn giúp em với ;-;
Gửi Hủy 
- SANS:))$$^
-
5. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3. 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức : N = a + b. 7. Cho a, b, c là các số dương. Chứng minh : a3 + b3 + abc ≥ ab(a + b + c) 8. Tìm liên hệ giữa các số a và b biết rằng : |a+b|>|a-b| 9. a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a b) Cho a, b, c > 0 và abc = 1. Chứng minh : (a + 1)(b + 1)(c + 1) ≥ 8 10. Chứng minh các bất đẳng thức: a) (a + b)2 ≤ 2(a2 + b2) b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Xem chi tiết Lớp 9 Toán Câu hỏi của OLM 2 0 Gửi Hủy 
Khổng Nguyễn Ngân Dương 25 tháng 2 2022 lúc 18:40 ấn vào ô báo cáo
Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy 
Phan Tuấn Anh 25 tháng 2 2022 lúc 22:31 Tối quá, ko thấy bài đâu
HT
Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy Khoá học trên OLM (olm.vn)
- Toán lớp 8 (Kết nối tri thức với cuộc sống)
- Toán lớp 8 (Cánh Diều)
- Toán lớp 8 (Chân trời sáng tạo)
- Ngữ văn lớp 8 (Kết nối tri thức với cuộc sống)
- Ngữ văn lớp 8 (Cánh Diều)
- Ngữ văn lớp 8 (Chân trời sáng tạo)
- Tiếng Anh lớp 8 (i-Learn Smart World)
- Tiếng Anh lớp 8 (Global Success)
- Khoa học tự nhiên lớp 8 (Kết nối tri thức với cuộc sống)
- Khoa học tự nhiên lớp 8 (Cánh diều)
- Khoa học tự nhiên lớp 8 (Chân trời sáng tạo)
- Lịch sử và địa lý lớp 8 (Kết nối tri thức với cuộc sống)
- Lịch sử và địa lý lớp 8 (Cánh diều)
- Lịch sử và địa lý lớp 8 (Chân trời sáng tạo)
- Giáo dục công dân lớp 8 (Kết nối tri thức với cuộc sống)
- Giáo dục công dân lớp 8 (Cánh diều)
- Giáo dục công dân lớp 8 (Chân trời sáng tạo)
- Công nghệ lớp 8 (Kết nối tri thức với cuộc sống)
Từ khóa » Cho A3 + B3 = 2. Chứng Minh Rằng A + B ≤ 2
-
Cho A^3 + B^3 = 2. Chứng Minh Rằng A + B ≤ 2 - Toán Học Lớp 9
-
Cho A3 + B3 = 2. Chứng Minh Rằng A + B ≤ 2 - Olm
-
Cho A3 + B3 = 2. Chứng Minh Rằng A + B ≤ 2. Câu Hỏi 894473
-
Cho A3 + B3 = 2. Chứng Minh Rằng A + B ≤ 2. - MTrend
-
Cho A3+b3=2 . Chứng Minh Rằng A+b - Hoc24
-
Cho A3 +b3 =2 Tìm Giá Trị Lớn Nhất Của Biểu Thức A = A +b
-
1) Cho \(a^3+b^3=2\) Chứng Minh Rằng \(a+b\le2\)( Gợi ý
-
Bài Tập ôn Thi Học Sinh Giỏi Môn Toán Lớp 9 - Thư Viện Đề Thi
-
Các Phương Pháp Giải Toán Lớp 9 - Tài Liệu Text - 123doc
-
(DOC) CHUYÊN ĐỀ BỒI DƯỠNG HỌC SINH GIỎI
-
[PDF] CHUYÊN ĐỀ: BẤT ĐẲNG THỨC
-
Bài Tập Bất đẳng Thức Và Bất đẳng Thức Cauchy