Cho đường Tròn (O;R) Và đường Thẳng D, độ Dài đường Vuông Góc ...

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng

• Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn

Đóng Đăng nhập Đăng ký

Lớp học

• Lớp 12
• Lớp 11
• Lớp 10
• Lớp 9
• Lớp 8
• Lớp 7
• Lớp 6
• Lớp 5
• Lớp 4
• Lớp 3
• Lớp 2
• Lớp 1

Môn học

• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Đạo đức
• Tự nhiên và xã hội
• Khoa học
• Lịch sử và Địa lý
• Tiếng việt
• Khoa học tự nhiên
• Hoạt động trải nghiệm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng

• Tất cả
• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Hãy tham gia nhóm Học sinh Hoc24OLM Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Câu hỏi

Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay thủy bùi 17 tháng 11 2018 lúc 23:28 Cho đường tròn (O;R) và đường thẳng d, độ dài đường vuông góc OH từ O đến đường thẳng d bằng 2R. Gọi M là một điểm bất kì nằm trên đường thẳng d, kẻ các tiếp tuyến MA, MB với đường tròn (O), A và B là các tiếp điểm. Đoạn thẳng AB cắt OM, OH theo thứ tự C và D. a) Chứng minh: tam giác OCD và OHM đồng dạng b) OM cắt (O) tại I. chứng minh: OC.OMOI2 c) khi điểm M di động trên đường thẳng d thì điểm C di động trên đường thẳng nào? vì saoĐọc tiếp

Cho đường tròn (O;R) và đường thẳng d, độ dài đường vuông góc OH từ O đến đường thẳng d bằng 2R. Gọi M là một điểm bất kì nằm trên đường thẳng d, kẻ các tiếp tuyến MA, MB với đường tròn (O), A và B là các tiếp điểm. Đoạn thẳng AB cắt OM, OH theo thứ tự C và D.

a) Chứng minh: tam giác OCD và OHM đồng dạng

b) OM cắt (O) tại I. chứng minh: OC.OM=OI2

c) khi điểm M di động trên đường thẳng d thì điểm C di động trên đường thẳng nào? vì sao

Lớp 9 Toán Ôn tập Đường tròn Những câu hỏi liên quan

• Bình Phạm

27 tháng 10 2021 lúc 15:15

Cho đường tròn(o,r) từ một điểm A trên (o). trên đường thẳng d lấy điểm M bất kì (M khác A ) kẻ các tuyến MNP và gọi K Là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). kẻ AC vuông góc với MB ,BP vuông góc với MA gọi H là giao điểm của AC và AB ,I là giao điểm của OM và AB ,I là giao điểm của OM và AB

Xem chi tiết Lớp 9 Toán 0 0 Gửi Hủy

• Nguyễn Thị Hương
• 

19 tháng 3 2022 lúc 11:49 Cho đường tròn (O,R) và đường thẳng d cố định, d không có điểm chung với đường tròn. Gọi M là điểm thuộc đường thẳng d. Qua M kẻ hai tiếp tuyến MA,MB với đường tròn (A,B là các tiếp điểm). Từ O kẻ OH vuông góc với đường thẳng d (H thuộc d). Nối A với B, AB cắt OH tại K và cắt OM taị I. Gọi E là tâm đường tròn nội tiếp Δ MAB. Giả sử R 6 cm và góc AMB 60 độ. Tính bán kính đường tròn nội tiếp Δ MABĐọc tiếp

Cho đường tròn (O,R) và đường thẳng d cố định, d không có điểm chung với đường tròn. Gọi M là điểm thuộc đường thẳng d. Qua M kẻ hai tiếp tuyến MA,MB với đường tròn (A,B là các tiếp điểm). Từ O kẻ OH vuông góc với đường thẳng d (H thuộc d). Nối A với B, AB cắt OH tại K và cắt OM taị I. Gọi E là tâm đường tròn nội tiếp Δ MAB. Giả sử R = 6 cm và góc AMB = 60 độ. Tính bán kính đường tròn nội tiếp Δ MAB

Xem chi tiết Lớp 9 Toán Chương II - Đường tròn 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 12 tháng 1 2024 lúc 22:25

Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MO là phân giác của góc AMB và MA=MB

MO là phân giác của góc AMB

=>\(\widehat{AMO}=\dfrac{\widehat{AMB}}{2}=\dfrac{60^0}{2}=30^0\)

Xét ΔOAM vuông tại A có \(tanAMO=\dfrac{OA}{AM}\)

=>\(\dfrac{6}{AM}=tan30=\dfrac{\sqrt{3}}{3}\)

=>\(AM=6\cdot\dfrac{3}{\sqrt{3}}=6\sqrt{3}\left(cm\right)\)

Xét ΔMAB có MA=MB và \(\widehat{AMB}=60^0\)

nên ΔMAB đều

=>\(\widehat{MBA}=60^0\)

Gọi bán kính đường tròn nội tiếp ΔMAB là d

Diện tích tam giác MBA là:

\(S_{MBA}=\dfrac{1}{2}\cdot MA\cdot MB\cdot sinAMB\)

\(=\dfrac{1}{2}\cdot6\sqrt{3}\cdot6\sqrt{3}\cdot sin60=27\sqrt{3}\left(cm^2\right)\)

Nửa chu vi tam giác MBA là:

\(p=\dfrac{6\sqrt{3}+6\sqrt{3}+6\sqrt{3}}{2}=3\sqrt{3}\left(cm\right)\)

Xét ΔMBA có \(S_{MBA}=p\cdot d\)

=>\(d=\dfrac{27\sqrt{3}}{3\sqrt{3}}=9\left(cm\right)\)

Đúng 0 Bình luận (0) Gửi Hủy

• Le Xuan Mai

2 tháng 12 2023 lúc 22:11 cho đường tròn (O;R) từ một điểm A trên (O) kẻ tiếp tuyến d với(o).Trên đường thẳng (d)lấy điểm M bất kì (M khác A)kẻ cát tuyến MNP và gọi K là trung điểm của NP,kẻ tiếp tuyến MB(B là tiếp điểm).Kẻ AC vuông góc NB,BD vuông góc MA ,gọi H là giao điểm của AC và BD ,I là giao điểm của OM và AB.A. chứng minh năm điểm O,K,A,M,B cùng nằm trên một đường trònb.chứng minh OI.OMR2;OI.IMIA2C.chứng minh OAHB là hình thoid.chứng minh ba điểm 0,H,M thẳng hàngĐọc tiếp

cho đường tròn (O;R) từ một điểm A trên (O) kẻ tiếp tuyến d với(o).Trên đường thẳng (d)lấy điểm M bất kì (M khác A)kẻ cát tuyến MNP và gọi K là trung điểm của NP,kẻ tiếp tuyến MB(B là tiếp điểm).Kẻ AC vuông góc NB,BD vuông góc MA ,gọi H là giao điểm của AC và BD ,I là giao điểm của OM và AB.

A. chứng minh năm điểm O,K,A,M,B cùng nằm trên một đường tròn

b.chứng minh OI.OM=R2;OI.IM=IA2

C.chứng minh OAHB là hình thoi

d.chứng minh ba điểm 0,H,M thẳng hàng

Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 2 tháng 12 2023 lúc 22:26

a: ΔONP cân tại O

mà OK là đường trung tuyến

nên OK\(\perp\)NP tại K

Ta có: \(\widehat{OAM}=\widehat{OBM}=\widehat{OKM}=90^0\)

=>O,A,M,B,K cùng thuộc đường tròn đường kính OM

b: Xét (O) có

MA,MB là tiếp tuyến

Do đó: MA=MB

=>M nằm trên đường trung trực của BA(1)

OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1) và (2) suy ra MO là đường trung trực của AB

=>MO\(\perp\)AB tại H và H là trung điểm của AB

Xét ΔOAM vuông tại A có AI là đường cao

nên \(OI\cdot OM=OA^2=R^2\)

Xét ΔOAM vuông tại A có AI là đường cao

nên \(OI\cdot IM=IA^2\)

c: AC\(\perp\)BM

OB\(\perp\)BM

Do đó: OB//AC

=>OB//AH

BD\(\perp\)MA

OA\(\perp\)MA

Do đó: BD//OA

=>BH//OA

Xét tứ giác OBHA có

OB//HA

OA//HB

Do đó: OBHA là hình bình hành

Hình bình hành OBHA có OB=OA

nên OBHA là hình thoi

d: OBHA là hình thoi

=>OH là đường trung trực của BA

mà M nằm trên đường trung trực của BA(cmt)

nên O,H,M thẳng hàng

Đúng 1 Bình luận (0) Gửi Hủy

• Hà Việt Hùng

24 tháng 1 2021 lúc 19:25 Bài 14: Cho đường tròn (O;R) Lấy M cách O một khoảng cách 2R. Từ M kẻ các tiếp tuyến MA và MB với đường tròn (A và B là các tiếp điểm). Đoạn thẳng OM cắt đường tròn (O) tại C. Đường Thẳng qua O và vuông góc với OB cắt OA tại D. Đường thẳng DC cắt MB tại điểm E.a) Chứng minh Tam giác MAB là Tam giác đềub) Chứng minh rằng Tam giác DMO cân tại Dc) Chứng minh rằng DE là tiếp tuyến của đường tròn (O)  Đọc tiếp

Bài 14: Cho đường tròn (O;R) Lấy M cách O một khoảng cách = 2R. Từ M kẻ các tiếp tuyến MA và MB với đường tròn (A và B là các tiếp điểm). Đoạn thẳng OM cắt đường tròn (O) tại C. Đường Thẳng qua O và vuông góc với OB cắt OA tại D. Đường thẳng DC cắt MB tại điểm E.

a) Chứng minh Tam giác MAB là Tam giác đều

b) Chứng minh rằng Tam giác DMO cân tại D

c) Chứng minh rằng DE là tiếp tuyến của đường tròn (O)

 

 

Xem chi tiết Lớp 9 Toán Ôn tập Đường tròn 1 1 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 24 tháng 1 2021 lúc 20:04

a) Xét (O) có

MA là tiếp tuyến có A là tiếp điểm(gt)

MB là tiếp tuyến có B là tiếp điểm(gt)

Do đó: MA=MB(Tính chất hai tiếp tuyến cắt nhau)

Xét (O) có

MA là tiếp tuyến có A là tiếp điểm(gt)

MB là tiếp tuyến có B là tiếp điểm(gt)

Do đó: MO là tia phân giác của \(\widehat{AMB}\)(Tính chất hai tiếp tuyến cắt nhau)

nên \(\widehat{AMB}=2\cdot\widehat{AMO}\)(1)

Xét ΔOAM vuông tại A có 

\(\sin\widehat{AMO}=\dfrac{OA}{OM}=\dfrac{R}{2\cdot R}=\dfrac{1}{2}\)

hay \(\widehat{AMO}=30^0\)(2)

Thay (2) vào (1), ta được: \(\widehat{AMB}=60^0\)

Xét ΔAMB có MA=MB(cmt)

nên ΔAMB cân tại M(Định nghĩa tam giác cân)

Xét ΔAMB cân tại M có \(\widehat{AMB}=60^0\)(cmt)

nên ΔAMB đều(Dấu hiệu nhận biết tam giác đều)

 

Đúng 1 Bình luận (0) Gửi Hủy

• hoàng tử gió 2k7

1 tháng 2 2022 lúc 21:19 cho đường tròn tâm O bán kinh R và một đường thẳng (d) cố định, (d) và đường tròn (O;R) không giao nhau. gọi H là chân đường vuông góc kẻ từ (O)  đến đường thẳng (d), M là một điểm ko thay đổi trên (d)(M ko trùng với H). từ M kẻ hai tiếp tuyến MA, MB với đường tròn (A,B là tiếp điểm). Dây cung AB cắt OH tại I. a.cm O,A,B,H,M cung nằm trên một đường trònb.cm khi M thay đổi trên (d) thì AB luôn đi qua một điểm cố địnhĐọc tiếp

cho đường tròn tâm O bán kinh R và một đường thẳng (d) cố định, (d) và đường tròn (O;R) không giao nhau. gọi H là chân đường vuông góc kẻ từ (O)  đến đường thẳng (d), M là một điểm ko thay đổi trên (d)(M ko trùng với H). từ M kẻ hai tiếp tuyến MA, MB với đường tròn (A,B là tiếp điểm). Dây cung AB cắt OH tại I. 

a.cm O,A,B,H,M cung nằm trên một đường tròn

b.cm khi M thay đổi trên (d) thì AB luôn đi qua một điểm cố định

Xem chi tiết Lớp 9 Toán Violympic toán 9 1 0 Gửi Hủy Nguyễn Huy Tú 1 tháng 2 2022 lúc 21:26

a, Vì MA ; MB là tiếp tuyến đường tròn (O) với A;B là tiếp điểm 

=> ^OAM = ^OBM = 900

Xét tứ giác AMBO có : 

^OAM + ^OBM = 1800

mà 2 góc này đối 

Vậy tứ giác AMBO là tứ giác nt 1 đường tròn (1) 

Xét tứ giác OHMB có : 

^OHM + ^MBO = 1800 

mà 2 góc này đối 

Vậy tứ giác OHMB là tứ giác nt 1 đường tròn (2) 

mà 2 tứ giác cùng chứa tam giác OBM (3) 

Từ (1) ; (2) ; (3) vậy O;A;B;H;M cùng nằm trên 1 đường tròn 

 

Đúng 1 Bình luận (5) Gửi Hủy

• hoàng tử gió 2k7

6 tháng 2 2022 lúc 20:49

cho đường tròn tâm O bán kinh R và một đường thẳng (d) cố định, (d) và đường tròn (O;R) không giao nhau. gọi H là chân đường vuông góc kẻ từ (O)  đến đường thẳng (d), M là một điểm ko thay đổi trên (d)(M ko trùng với H). từ M kẻ hai tiếp tuyến MA, MB với đường tròn (A,B là tiếp điểm). Dây cung AB cắt OH tại I. 

cm khi M thay đổi trên (d) thì AB luôn đi qua một điểm cố định

Xem chi tiết Lớp 9 Toán Violympic toán 9 0 0 Gửi Hủy

• Big City Boy

20 tháng 5 2022 lúc 12:09

Cho (O;R) và điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm). Kẻ đường kính AD của đường tròn (O;R), gọi K là hình chiếu vuông góc của B trên đường thẳng AD. Gọi I là trung điểm của đoạn thẳng BK. Chứng minh: ba điểm M, I, D thẳng hàng

Xem chi tiết Lớp 9 Toán Violympic toán 9 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 14 tháng 6 2023 lúc 18:37

    

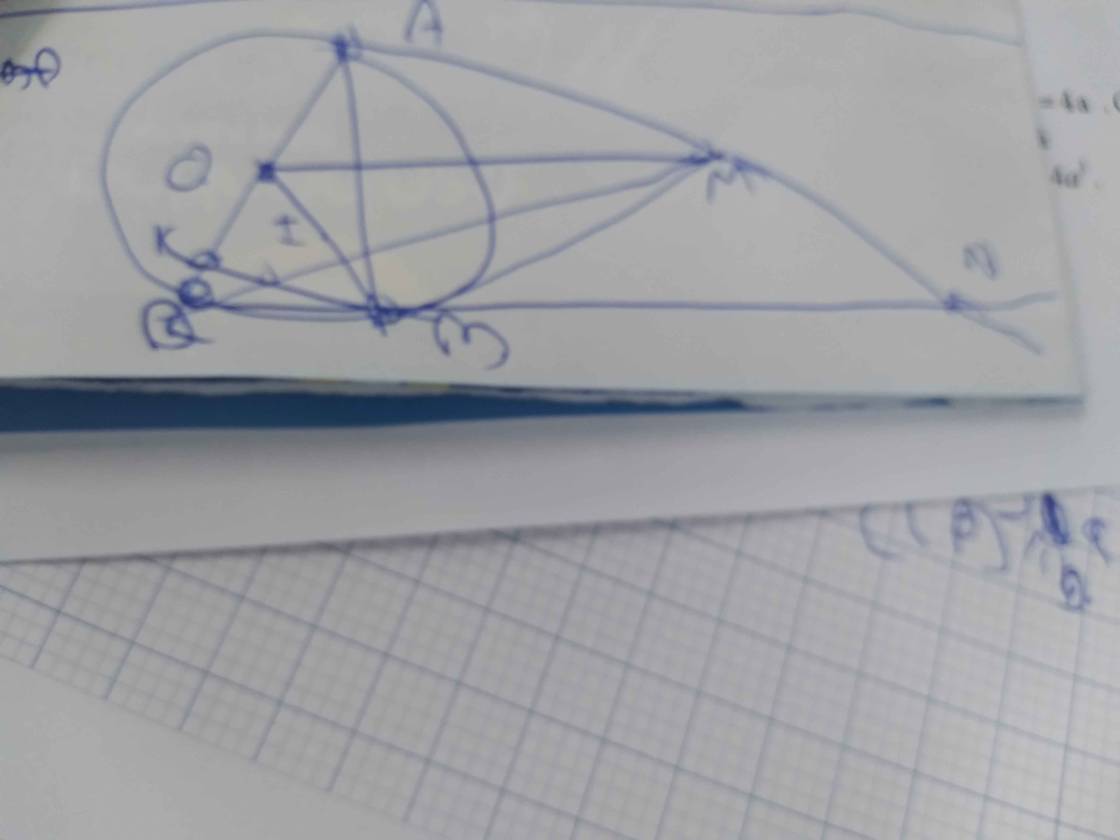
Đúng 0 Bình luận (0) Gửi Hủy

• Phở Ryou

28 tháng 12 2020 lúc 14:57 Cho đường tròn (O; R) và đường thẳng d không có điểm chung sao cho khoảng cách từ O đến d không quá 2R. Qua diêm M trên d, vẽ các tiếp tuyến MA, MB tới (O) với A, B là các tiếp điểm. Gọi H là hình chiếu vuông góc của O trên d. Vẽ Dây AB cắt OH ở K và cắt OM tại I. Tia OM cắt (O) tại E.a. Chứng minh 5 điểm O,A,M,B,H cùng thuộc 1 đường trònb.Chứng minh OI.OMR2c. Chứng minh OK.OH OI.OMd. Tìm vị trí của M trên d để OAEB là hình thoie. Khi M di chuyên trên d. Chứng minh đường thẳng AB luôn đi qua mộ...Đọc tiếp

Cho đường tròn (O; R) và đường thẳng d không có điểm chung sao cho khoảng cách từ O đến d không quá 2R. Qua diêm M trên d, vẽ các tiếp tuyến MA, MB tới (O) với A, B là các tiếp điểm. Gọi H là hình chiếu vuông góc của O trên d. Vẽ Dây AB cắt OH ở K và cắt OM tại I. Tia OM cắt (O) tại E.a. Chứng minh 5 điểm O,A,M,B,H cùng thuộc 1 đường trònb.Chứng minh OI.OM=R2c. Chứng minh OK.OH = OI.OMd. Tìm vị trí của M trên d để OAEB là hình thoie. Khi M di chuyên trên d. Chứng minh đường thẳng AB luôn đi qua một điểm cố định

Xem chi tiết Lớp 9 Toán Chương II - Đường tròn 0 1 Gửi Hủy

• Gia Huy Nguyen

27 tháng 12 2021 lúc 14:48

Cho đường tròn (O; R) và một điểm A nằm bên ngoài đường tròn đó. Qua A kẻ đường thẳng d vuông góc với OA, trên đường thẳng d lấy một điểm M bất kì (M khác A). Từ M kẻ tiếp tuyến MB, MC tới đường tròn (O).

a) C/m tứ giác MBOC nội tiếp được đường tròn

b) MO cắt BC tại H, c/m OM.OH=R2

c) Khi điểm M thay đổi trên d, c/m BC luônđi qua một điểm cố định

Xem chi tiết Lớp 9 Toán 1 1 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 27 tháng 12 2021 lúc 18:40

a: Xét tứ giác MBOC có

\(\widehat{MBO}+\widehat{MCO}=180^0\)

Do đó: MBOC là tứ giác nội tiếp

Đúng 0 Bình luận (0) Gửi Hủy

• Trần Vũ Minh Huy
• 

22 tháng 10 2023 lúc 14:15 Cho đường tròn O bán kính R,từ 1 điểm A trên đường tròn kẻ tiếp tuyến d với đường kính O.Trên đường thẳng d lấy điểm M bất kì(M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP,kẻ tiếp tuyến MB(P là tiếp điểm).Kẻ AC vuông góc với MB,BD vuông góc với MA, gọi H là giao điểm của AC và BD I là giao điểm OM và AB1. CM tứ giác AMBO nội tiếp.2. CM năm điểm O,K,A,K,B cùng nàm trên một đường tròn  Đọc tiếp

Cho đường tròn O bán kính R,từ 1 điểm A trên đường tròn kẻ tiếp tuyến d với đường kính O.Trên đường thẳng d lấy điểm M bất kì(M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP,kẻ tiếp tuyến MB(P là tiếp điểm).Kẻ AC vuông góc với MB,BD vuông góc với MA, gọi H là giao điểm của AC và BD I là giao điểm OM và AB1. CM tứ giác AMBO nội tiếp.2. CM năm điểm O,K,A,K,B cùng nàm trên một đường tròn

 

 

Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 22 tháng 10 2023 lúc 14:26

1: Xét tứ giác AMBO có

\(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)

=>AMBO là tứ giác nội tiếp đường tròn đường kính OM

2: ΔONP cân tại O

mà OK là trung tuyến

nên OK vuông góc NP

\(\widehat{OKM}=\widehat{OAM}=\widehat{OBM}=90^0\)

=>O,K,A,M,B cùng thuộc 1 đường tròn

Đúng 1 Bình luận (0) Gửi Hủy

Khoá học trên OLM (olm.vn)

• Toán lớp 9
• Ngữ văn lớp 9
• Tiếng Anh lớp 9
• Vật lý lớp 9
• Hoá học lớp 9
• Sinh học lớp 9
• Lịch sử lớp 9
• Địa lý lớp 9