Cho Hình Chóp S.ABCD Có đáy ABCD Là Hình Vuông Cạnh A.SA ...
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
 Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay Diệu Hà Khổng 3 tháng 3 2020 lúc 19:29
Diệu Hà Khổng 3 tháng 3 2020 lúc 19:29 cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a.SA vuông góc với (ABCD) và SA=a
a)Tính góc giữa SB và mp (SAC)
b)Tính góc giữa CA và mp(SCD) và góc giữa DB và mp(SDC)
Lớp 11 Toán Chương 3: VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓ... Những câu hỏi liên quan
- Yeon Park
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a; AD= 2a; SA vuông góc với đáy, SA=a√2. Xác định và tính góc giữa. a) Các đường thẳng SB, SC, SD với mp đáy. b) SC với các mp (SAD) và ( SAB). c) SA với mp (SCD). d) SB và (SAC).
Xem chi tiết Lớp 11 Toán 1 0 Gửi Hủy
Gửi Hủy  Ami Mizuno
Ami Mizuno  13 tháng 3 2022 lúc 16:11
13 tháng 3 2022 lúc 16:11 


 Gửi Hủy
Gửi Hủy 
- Nguyễn Thu Trang
Cho hình chóp S.ABCD đáy là hình vuông cạnh a , tâm O. SA vuông góc với đáy và S4=a căn 6. 1) Chứng minh SB L BC 2) Tính góc giữa SD và mp(ABCD) 3) Tính góc giữa mp(SBC) và mp(ABCD) 4) Tỉnh khoảng cách từ O đến mp(SCD) 5) Tính khoảng cách giữa hai đường thẳng SB và AC
Xem chi tiết Lớp 11 Toán Chương 2: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIA... 1 0 Gửi Hủy
Gửi Hủy  Nguyễn Lê Phước Thịnh CTV
Nguyễn Lê Phước Thịnh CTV  7 tháng 7 2023 lúc 10:09
7 tháng 7 2023 lúc 10:09 1: AC=căn a^2+a^2=a*căn 2
=>SC=căn SA^2+AC^2=a*căn 8
SB=căn AB^2+SA^2=a*căn 7
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
=>SB vuông góc BC
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Nguyễn Hoàng Anh
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB. SA vuông góc với (ABCD) a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
Xem chi tiết Lớp 11 Toán Bài 4: Hai mặt phẳng vuông góc 4 1 Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  3 tháng 3 2022 lúc 23:54
3 tháng 3 2022 lúc 23:54 c.
Từ câu b ta có AICD là hình vuông \(\Rightarrow CI\perp AB\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CI\)
\(\Rightarrow CI\perp\left(SAB\right)\)
Lại có \(CI\in\left(SCI\right)\Rightarrow\left(SCI\right)\perp\left(SAB\right)\)
d.
I là trung điểm AB \(\Rightarrow CI\) là trung tuyến ứng với AB
Lại có \(CI=AD=a\) (AICD là hình vuông) \(\Rightarrow CI=\dfrac{1}{2}AB\)
\(\Rightarrow\Delta ACB\) vuông tại C
\(\Rightarrow BC\perp AC\) (1)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAC\right)\)
\(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAC\right)\)
Đúng 2 Bình luận (0) Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  3 tháng 3 2022 lúc 23:55
3 tháng 3 2022 lúc 23:55 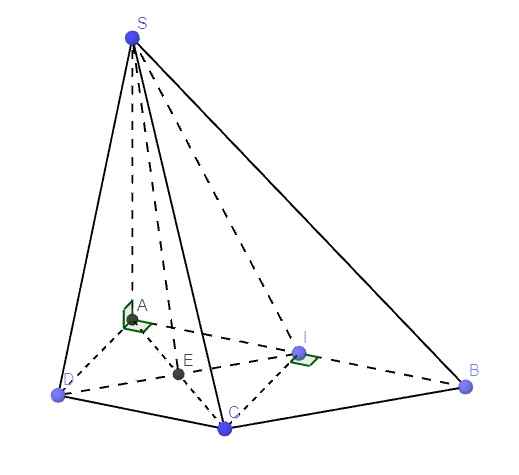
 Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  3 tháng 3 2022 lúc 23:57
3 tháng 3 2022 lúc 23:57 a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)
Đúng 2 Bình luận (1) Gửi Hủy Xem thêm câu trả lời
Gửi Hủy Xem thêm câu trả lời 
- Meo Con Nguyen
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SA=a\(\sqrt{2}\)
a) CMR các mặt bên của hình chóp là những tam giác vuông.
b) CMR (SAC) vuông góc với (SBD)
c)Tính góc giữa SC và mp (SAB)
d)Tính góc giữa hai mp(SBD) và (ABCD)
e)Tính khoảng cách giữa điểm A và mp (SCD).
Xem chi tiết Lớp 11 Toán Bài 5: Khoảng cách 4 0
 Gửi Hủy
Gửi Hủy  Hồng Trinh 23 tháng 5 2016 lúc 22:38
Hồng Trinh 23 tháng 5 2016 lúc 22:38 a. Ta có : \(\begin{cases}AB\perp BC\left(ABCDvuong\right)\\SA\perp BC\left(SA\perp\left(ABCD\right)\right)\end{cases}\) \(\Rightarrow BC\perp\left(SAB\right)\) mà \(SB\subset\left(SAB\right)\) nên \(BC\perp SB\) Vậy \(\Delta SBC\left(\perp B\right)\)
tương tự ta có : \(\begin{cases}SA\perp DC\\AD\perp DC\end{cases}\) \(\Rightarrow DC\perp\left(SAD\right)\) mà \(SD\subset\left(SAD\right)\) nên \(SD\perp DC\) Vậy \(\Delta SDC\left(\perp D\right)\)
ta có \(SA\perp AD\) nên \(\Delta SAD\left(\perp A\right)\)
Có \(SA\perp AB\) nên \(\Delta SAB\left(\perp A\right)\)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy  Hồng Trinh 23 tháng 5 2016 lúc 22:43
Hồng Trinh 23 tháng 5 2016 lúc 22:43 b. Ta có : \(\begin{cases}AC\perp BD\\SA\perp BD\end{cases}\) \(\Rightarrow BD\perp\left(SAC\right)\) mà \(BD\subset\left(SBD\right)\) nên \(\left(SAC\right)\perp\left(SBD\right)\)
Đúng 0 Bình luận (0)
 Gửi Hủy
Gửi Hủy  Hồng Trinh 23 tháng 5 2016 lúc 22:51
Hồng Trinh 23 tháng 5 2016 lúc 22:51 c. Ta có : \(CB\perp\left(SAB\right)\) Hình chiếu vuông góc của SC lên (SAB) là SB nên góc giữa SC và (SAB) là \(\widehat{CSB}\)
Xét \(\Delta SAB\left(\perp A\right)\) ta có : Theo Pytago: \(SB^2=SA^2+AB^2\Leftrightarrow SB=\sqrt{2a^2+a^2}=a\sqrt{3}\)
Xét \(\Delta SBC\left(\perp B\right)\) ta có \(tan\widehat{CSB}=\frac{CB}{SB}=\frac{a}{a\sqrt{3}}\) \(\Rightarrow\widehat{BSC}=30^o\)
Đúng 0 Bình luận (0) Gửi Hủy Xem thêm câu trả lời
Gửi Hủy Xem thêm câu trả lời 
- Nguyễn Hoàng Anh
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
Xem chi tiết Lớp 11 Toán Bài 4: Hai mặt phẳng vuông góc 1 1 Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  3 tháng 3 2022 lúc 19:44
3 tháng 3 2022 lúc 19:44 Đề bài thiếu chi tiết định dạng điểm S nên không giải được (ví dụ phải thêm SA vuông góc mặt đáy hoặc gì đó tương tự)
Đúng 0 Bình luận (1) Gửi Hủy
Gửi Hủy 
- Thúy Nga
Cho hình chóp S.ABCD với ABCD là hình vuông cạnh a ,SA vuông góc với đáy, SA=a. Tính góc giữa 2 mp (SAB) và (SCD)
Xem chi tiết Lớp 11 Toán Chương 3: VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓ... 0 0 Gửi Hủy
Gửi Hủy 
- only bachtuyet1999
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a , SA vuông góc ABCD , SA =a√2 a) CM : BD vuông góc SAC b) tính góc giữa SC và mp ABCD
 Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  11 tháng 3 2022 lúc 0:55
11 tháng 3 2022 lúc 0:55 25.
\(\lim\dfrac{3.5^n+7.7^n+9}{6.5^n+9.7^n-3}=\lim\dfrac{7^n\left[3\left(\dfrac{5}{7}\right)^n+7+9.\left(\dfrac{1}{7}\right)^n\right]}{7^n\left[6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n\right]}\)
\(=\lim\dfrac{3\left(\dfrac{5}{7}\right)^n+7+9\left(\dfrac{1}{7}\right)^n}{6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n}=\dfrac{3.0+7+9.0}{6.0+9-3.0}=\dfrac{7}{9}\)
26.
\(\lim\left(n-\sqrt{n^2-4n}\right)=\lim\dfrac{\left(n-\sqrt{n^2-4n}\right)\left(n+\sqrt{n^2-4n}\right)}{n+\sqrt{n^2-4n}}\)
\(=\lim\dfrac{4n}{n+\sqrt{n^2-4n}}=\lim\dfrac{4n}{n\left(1+\sqrt{1-\dfrac{4}{n}}\right)}\)
\(=\lim\dfrac{4}{1+\sqrt{1-\dfrac{4}{n}}}=\dfrac{4}{1+\sqrt{1-0}}=2\)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  11 tháng 3 2022 lúc 1:01
11 tháng 3 2022 lúc 1:01 26.
\(u_1=5\)
\(u_n=405=u_1.q^{n-1}\Rightarrow q^{n-1}=\dfrac{405}{5}=81\)
\(\Rightarrow q^n=81q\)
Do \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}\Rightarrow605=\dfrac{5\left(1-81q\right)}{1-q}\)
\(\Rightarrow605-605q=5-405q\)
\(\Rightarrow q=3\)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  11 tháng 3 2022 lúc 1:07
11 tháng 3 2022 lúc 1:07 27.
a.
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow BD\perp\left(SAC\right)\)
b.
Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
Đúng 0 Bình luận (0) Gửi Hủy Xem thêm câu trả lời
Gửi Hủy Xem thêm câu trả lời 
- B13_03_Nguyễn Trọng Cửu
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Cmr: CD vuông góc mp (SAD) b) Cmr: (SAC) vuông góc mp (SBD) c) Tính góc giữa SC v à mp (ABCD) d) Tính góc giữa mp ( SAB) và mp (SBC). e) Tính khoảng cách từ A đến mp ( SBD)
Xem chi tiết Lớp 11 Toán Chương 2: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIA... 1 0 Gửi Hủy
Gửi Hủy  Nguyễn Lê Phước Thịnh CTV
Nguyễn Lê Phước Thịnh CTV  15 tháng 6 2023 lúc 11:35
15 tháng 6 2023 lúc 11:35 a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- B13_03_Nguyễn Trọng Cửu
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD.
a) Cmr: CD vuông góc mp (SAD)
b) Cmr: (SAC) vuông góc mp (SBD)
c) Tính góc giữa SC v à mp (ABCD)
d) Tính góc giữa mp ( SAB) và mp (SBC).
e) Tính khoảng cách từ A đến mp ( SBD)
Xem chi tiết Lớp 11 Toán Chương 2: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIA... 1 1 Gửi Hủy
Gửi Hủy  Nguyễn Lê Phước Thịnh CTV
Nguyễn Lê Phước Thịnh CTV  15 tháng 6 2023 lúc 11:42
15 tháng 6 2023 lúc 11:42
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
c: (SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=căn 3
=>góc SCA=60 độ
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Tính góc giữa SC và mp (SAB).
Xem chi tiết Lớp 11 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  31 tháng 3 2017 lúc 9:58
31 tháng 3 2017 lúc 9:58 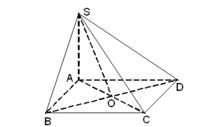
● BC ⊥ (SAB) ⇒ 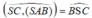
● ΔSAB vuông tại A 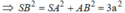
● ΔSBC vuông tại B 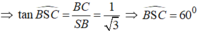
 Gửi Hủy
Gửi Hủy Khoá học trên OLM (olm.vn)
- Toán lớp 11 (Kết nối tri thức với cuộc sống)
- Toán lớp 11 (Cánh Diều)
- Toán lớp 11 (Chân trời sáng tạo)
- Ngữ văn lớp 11
- Tiếng Anh lớp 11 (i-Learn Smart World)
- Tiếng Anh lớp 11 (Global Success)
- Vật lý lớp 11 (Kết nối tri thức với cuộc sống)
- Vật lý lớp 11 (Cánh diều)
- Hoá học lớp 11 (Kết nối tri thức với cuộc sống)
- Hoá học lớp 11 (Cánh diều)
- Sinh học lớp 11 (Kết nối tri thức với cuộc sống)
- Sinh học lớp 11 (Cánh diều)
- Lịch sử lớp 11 (Kết nối tri thức với cuộc sống)
- Lịch sử lớp 11 (Cánh diều)
- Địa lý lớp 11 (Kết nối tri thức với cuộc sống)
- Địa lý lớp 11 (Cánh diều)
- Giáo dục kinh tế và pháp luật lớp 11 (Kết nối tri thức với cuộc sống)
- Tin học lớp 11 (Kết nối tri thức với cuộc sống)
- Công nghệ lớp 11 (Kết nối tri thức với cuộc sống)
Từ khóa » Góc Giữa Bd Và Sdc
-
Cho Hình Chóp (S.ABCD ) Có đáy (ABCD ) Là Hình Vuông. Mặt Bên
-
Tính Góc Giữa đường Thẳng SB Và Mp (SCD) Biết ABCD Là Hình Vuông
-
Góc Giữa đường Thẳng Và Mặt Phẳng
-
Góc Giữa đường Thẳng Và Mặt Phẳng
-
Cho Hình Chóp S.ABCD Có đáy Là Hình Vuông Cạnh A Và SA ...
-
A) SB Và (SAC). B) CẢ Và (SCD
-
B D ⊥ ( S A C ) - . B. Tính Góc Giữa SB Và (SAD). C. Tính Côsin Của ...
-
A) (SBC) Và (ABCD) B) (SCD) Và (ABCD) C) (SBC) Và (SCD) D) (SAB ...
-
Góc Giữa Hai Mặt Phẳng (SAB) Và (ABCD)
-
[PDF] CÁC VẤN ĐỀ VỀ GÓC (Phần 03) ĐÁP ÁN BÀI TẬP TỰ LUYỆN Giáo ...
-
Cách Xác Định Góc Giữa Đường Thẳng Và Mặt Phẳng Trong Không ...
-
BÀI TẬP KHOẢNG CÁCH VÀ GÓC Bài Toán... | Xem Lời Giải Tại QANDA
-
Hỏi đáp 24/7 – Giải Bài Tập Cùng Thủ Khoa