Cho M Thuộc Nửa đường Tròn đường Kính AB = 10cm, Tiếp Tuyến Ax ...
Có thể bạn quan tâm


Tìm kiếm với hình ảnh
Vui lòng chỉ chọn một câu hỏi
Tìm đáp án Đăng nhập
Đăng nhập- |
- Đăng ký


Hoidap247.com Nhanh chóng, chính xác
Hãy đăng nhập hoặc tạo tài khoản miễn phí!
Đăng nhậpĐăng ký

Lưu vào
+
Danh mục mới


- linhan157

- Chưa có nhóm
- Trả lời
48
- Điểm
427
- Cảm ơn
65
- Toán Học
- Lớp 9
- 60 điểm
- linhan157 - 23:05:56 18/12/2020
- Hỏi chi tiết
 Báo vi phạm
Báo vi phạm
Hãy luôn nhớ cảm ơn và vote 5* nếu câu trả lời hữu ích nhé!
TRẢ LỜI


- tantientuan100

- Chưa có nhóm
- Trả lời
6412
- Điểm
88665
- Cảm ơn
4630
- tantientuan100
- Câu trả lời hay nhất!

- 18/12/2020
 Đây là một chuyên gia không còn hoạt động
Đây là một chuyên gia không còn hoạt độngĐáp án:
Giải thích các bước giải:
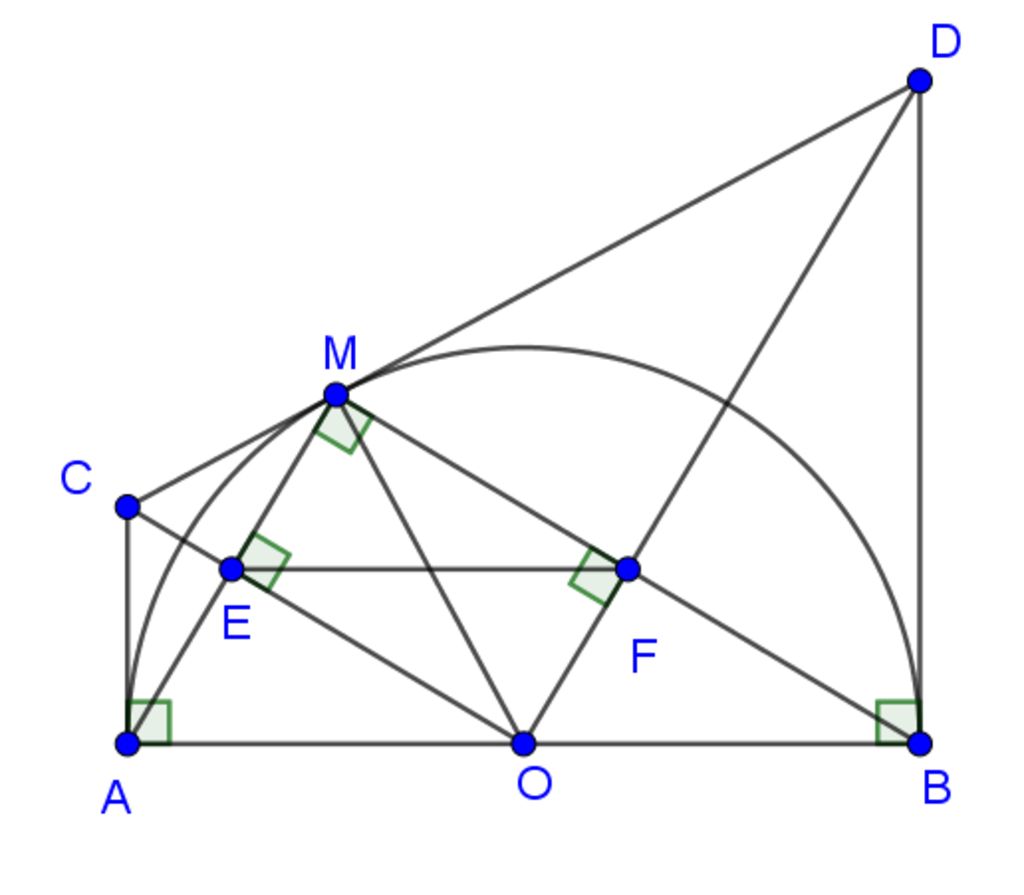
a)
Ta có $MC+MD=CD$
Mà:
$MC=AC$ (t/c 2 tiếp tuyến cắt nhau)
$MD=BD$ (t/c 2 tiếp tuyến cắt nhau)
Vậy $AC+BD=CD$
Ta có:
$OM=OA=R$
$CM=CA$ (t/c 2 tiếp tuyến cắt nhau)
$\to OC$ là đường trung trực của $MA$
$\to OC$ là tia phân giác $\widehat{MOA}$
CMTT: $OD$ là tia phân giác $\widehat{MOB}$
Mà $\widehat{MOA}$ và $\widehat{MOB}$ là hai góc kề bù
Nên $\widehat{COD}=90{}^\circ $
b)
$\Delta COD$ vuông tại $O$ có $OD$ là đường cao nên:
$O{{M}^{2}}=MC.MD$ (hệ thức lượng)
Mà
$O{{M}^{2}}={{R}^{2}}$
$MC=AC$ (t/c 2 tiếp tuyến cắt nhau)
$MD=BD$ (t.c 2 tiếp tuyến cắt nhau)
Vậy $AC.BD={{R}^{2}}$
c)
Vì $OC$ là đường trung trực của $MA$
Mà $OC$ cắt $MA$ tại $E$
$\to E$ là trung điểm $MA$
CMTT: $F$ là trung điểm $MB$
$\Delta MAB$ có $E,F$ lần lượt là trung điểm $MA,MB$
Nên $EF$ là đường trung bình của $\Delta MAB$
Do đó $EF=\frac{1}{2}AB=\frac{1}{2}.10=5\left( cm \right)$
- d)
Áp dụng bất đẳng thức $\operatorname{Cos}i$ ta có:
$M{{C}^{2}}+M{{D}^{2}}\ge 2MC.MD$
$M{{C}^{2}}+M{{D}^{2}}+2MC.MD\ge 4MC.MD$
${{\left( MC+MD \right)}^{2}}\ge 4{{R}^{2}}$
$C{{D}^{2}}\ge 4{{R}^{2}}\left( =const \right)$
Dấu $''=''$ xảy ra khi $MC=MD$
Hay $M$ là trung điểm $CD$
Vậy $M$ nằm trên nữa đường tròn $\left( O \right)$ sao cho $M$ là trung điểm $CD$ thì $CD$ nhỏ nhất
Hay ta có thể nói cách khác là M là điểm chính giữa của nữa đường tròn $\left(O\right)$
Hãy giúp mọi người biết câu trả lời này thế nào?

 Cảm ơn 2
Cảm ơn 2 Báo vi phạm
Báo vi phạm


- kiuchiuxiu

- We are trying
- Trả lời
266
- Điểm
767
- Cảm ơn
326
vào nhóm mik ko bn?
- kiuchiuxiu


- tantientuan100

- Chưa có nhóm
- Trả lời
6412
- Điểm
88665
- Cảm ơn
4630
làm thế nào để vào nhóm ?
- tantientuan100


- kiuchiuxiu

- We are trying
- Trả lời
266
- Điểm
767
- Cảm ơn
326
https://hoidap247.com/nhom-174 bạn vào link ở trên r bấm vào "Gửi yêu cầu" nhé^^
- kiuchiuxiu
Xem thêm:
- >> Tuyển tập 100+ đề bài đọc hiểu Ngữ Văn lớp 9
- Unavailable

- Chưa có nhóm
- Trả lời
14800
- Điểm
147
- Cảm ơn
15556
- Unavailable
- 18/12/2020

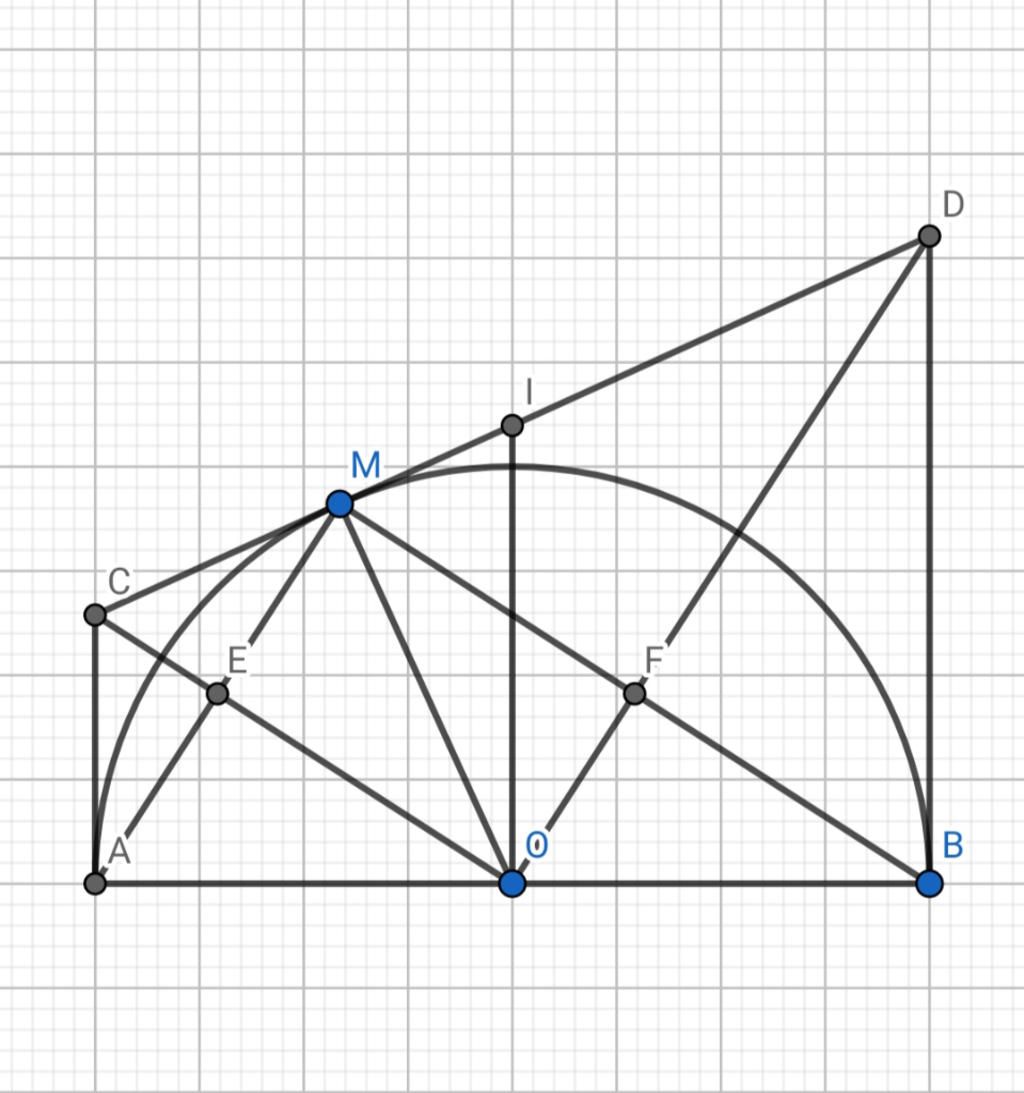
a) Ta có:
$CA;\, CM$ là tiếp tuyến của $(O)$ tại $A;\, M\quad (gt)$
$\to CA = CM$
Lại có:
$OA = OM = R$
$\to OC$ là trung trực của $AM$
$\to OC$ là phân giác của $\widehat{AOM}$
$\to \widehat{MOC}=\dfrac12\widehat{MOA}$
Chứng minh tương tự ta được:
$DB = DM$
$OD$ là trung trực của $BM$
$\widehat{MOD}=\dfrac12\widehat{MOB}$
Do đó:
$+)\quad AC + BD = CM + MD = CD$
$+)\quad \widehat{COD}=\widehat{MOC}+\widehat{MOD}$
$=\dfrac12(\widehat{MOA}+\widehat{MOB}$
$=\dfrac12\widehat{AOB}=90^\circ$
b) Ta có: $\widehat{COD}=90^\circ$
$\to ∆COD$ vuông tại $O$
Áp dụng hệ thức lượng trong $∆COD$ vuông tại $O$ đường cao $OM$ ta được:
$OM^2 = CM.DM$
$\to R^2 = AC.BD$
c) Ta có:
$OC$ là trung trực của $AM$ (câu a)
$OC\cap AM=\{E\}\quad (gt)$
$\to \widehat{MEO}=90^\circ$
Tương tự ta được: $\widehat{MFO}=90^\circ$
Xét tứ giác $MEOF$ có:
$\widehat{AMB}=\widehat{EMF}=90^\circ$ (góc nội tiếp chắn nửa đường tròn)
$\widehat{MEO}=\widehat{MFO}=90^\circ$
Do đó $MEOF$ là hình chữ nhật
$\to EF = OM = R =\dfrac12AB = 5\, cm$
d) Ta có:
$AC\perp AB\quad (gt)$
$BD\perp AB\quad (gt)$
$\to ABDC$ là hình thang vuông tại $A$ và $B$
Gọi $E$ là trung điểm $CD$
$\to OE$ là đường trung bình của hình thang $ABDC$
$\to \begin{cases}OE=\dfrac12(AC + BD)\\OE//AC//BD\end{cases}$
$\to \begin{cases}OE=\dfrac12CD\\OE\perp AB\end{cases}$
$\to CD \min \to OE\min$
Xét $∆MEO$ vuông tại $M$ luôn có:
$OE\geq OM$ (cạnh huyền $\geq$ cạnh góc vuông)
$\to OE \min = OM$
$\to E\equiv M$
$\to OM\perp AB$
$\to M$ là điểm chính giữa nửa đường tròn
Hãy giúp mọi người biết câu trả lời này thế nào?

 Cảm ơn 2
Cảm ơn 2 Báo vi phạm
Báo vi phạm


- linhan157

- Chưa có nhóm
- Trả lời
48
- Điểm
427
- Cảm ơn
65
Cháu cảm ơn chú!
- linhan157
Bạn muốn hỏi điều gì?
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí

Bảng tin
Bạn muốn hỏi điều gì?
Lý do báo cáo vi phạm?
Gửi yêu cầu Hủy

Cơ quan chủ quản: Công ty Cổ phần Công nghệ Giáo dục Thành Phát
Tải ứng dụng


- Hướng dẫn sử dụng
- Điều khoản sử dụng
- Nội quy hoidap247
- Góp ý
 Inbox: m.me/hoidap247online
Inbox: m.me/hoidap247online Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.
Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.
Từ khóa » Chứng Minh Góc Cod Bằng 90 độ
-
Chứng Minh Góc COD = 90 độ Và CD = AC + BD. Chứng Minh ... - Lazi
-
Chứng Minh Góc COD Bằng 90 độ Và CD = AC + BD - Toán Học Lớp 9
-
Chứng Minh CD = AC + BD Và Góc COD = 90 độ - Hoc247
-
Chứng Minh CD = AC + BD Và Góc COD = 90 độ - Nguyễn Ngọc Sơn
-
Chứng Minh AC + BD = CD. Chứng Minh Góc COD = 90 độ
-
Giúp Mình Bài Này Với Mấy Bạn ơi :<< Câu A Là CM : Góc COD = 90 ...
-
Cho Nửa đường Tròn Tâm O , đường Kính AB=2R , M Là Một điểm Tùy ...
-
Chứng Minh Góc COD Bằng 90 độ Và CD = AC + BD
-
Chứng Minh Góc COD = 90 độ. Chứng Minh CD = AC = BD
-
Góc COD = 90 độ Và AC . BD = R Bình Phươngc) Chứng Minh - Hoc24
-
Cho Nửa đường Tròn đường Kính AB = 2R. Từ A Và B Kẻ Hai Tiếp ...
-
Chứng Minh Tích AC + BD Không đổi
-
Bài Tập : Cho Nửa đường Tròn đg Kính AB = 2R .Từ A Và B Kẻ Tiếp ...