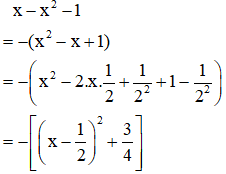Chứng Minh: A) X^2 – 2xy + Y^2 + 1 > 0 Với Mọi Số Thực X Và Y. B) X
Có thể bạn quan tâm
a) Ta có:
x2 – 2xy + y2 + 1
= (x2 – 2xy + y2) + 1
= (x – y)2 + 1.
(x – y)2 ≥ 0 với mọi x, y ∈ R
⇒ x2 – 2xy + y2 + 1 = (x – y)2 + 1 ≥ 0 + 1 = 1 > 0 với mọi x, y ∈ R (ĐPCM).
b) Ta có:
Ta có: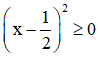 
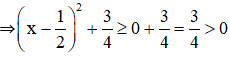
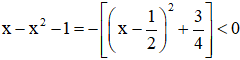
với mọi số thực x
⇒ 
với mọi số thực x
⇒ 
với mọi số thực (ĐPCM)
Từ khóa » Chứng Minh X^2+xy+y^2+1 0
-
Chứng Minh X^2+xy+y^2+1 > 0 Với Mọi X,y - HOC247
-
Chứng Minh X^2 + Xy + Y^2 + 1 > 0 Với Mọi X, Y - Phong Vu - Hoc247
-
Chứng Minh Rằng:x2-xy+y2+1>0 - Hoc24
-
CM: X2 + Xy + Y2 + 1 > 0 Với Mọi X , Y - Hoc24
-
CM: X2 + Xy + Y2 + 1 > 0 Với Mọi X , Y - Olm
-
Chung Minh:a,x2-2xy+y2+1>0 Với Mọi Số Thực X Và Yb,x-x2-1 - Olm
-
Chứng Minh Rằng X2 + Xy + Y2 + 1 > 0 Với Mọi X, Y - MTrend
-
Chứng Minh: 1) X^2 + Xy + Y^2 + 1 > 0 Với Mọi X, Y
-
Chứng Minh X2 + Xy + Y2 + 1 > 0 Với Mọi X, Y - Toán Học Lớp 8 - Lazi
-
Chứng Minh: X^2 – 2xy + Y^2 + 1 > 0 Với Mọi Số Thực X Và Y. - Khóa Học