Chứng Minh Tứ Giác Nội Tiếp

Tứ giác nội tiếp đường tròn

• A. Tứ giác nội tiếp là gì?
• B. Cách chứng minh tứ giác nội tiếp đường tròn
  • Phương pháp 1: Chứng minh bốn đỉnh của tứ giác cách đều 1 điểm
  • Phương pháp 2: Chứng minh tứ giác có hai góc đối diện bù nhau (tổng hai góc đối diện bằng 1800)
  • Phương pháp 3: Chứng minh hai đỉnh cùng nhìn đoạn thẳng tạo bởi hai điểm còn lại hai góc bằng nhau.
• C. Bài tập chứng minh tứ giác nội tiếp

Bài tập Toán 9: Chứng minh tứ giác nội tiếp đường tròn là một dạng toán hình xuất hiện nhiều trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

A. Tứ giác nội tiếp là gì?

- Tứ giác nội tiếp đường tròn là tứ giác có bôn đỉnh nằm trên một đường tròn. Đường tròn đó được gọi là đường tròn ngoại tiếp tứ giác.

B. Cách chứng minh tứ giác nội tiếp đường tròn

Phương pháp 1: Chứng minh bốn đỉnh của tứ giác cách đều 1 điểm

Ví dụ: Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt OM tại E, MB cắt nửa đường tròn (C) tại D (D khác B)

Chứng minh rằng: Tứ giác AMCO và AMDE là các tứ giác nội tiếp đường tròn.

Hướng dẫn giải

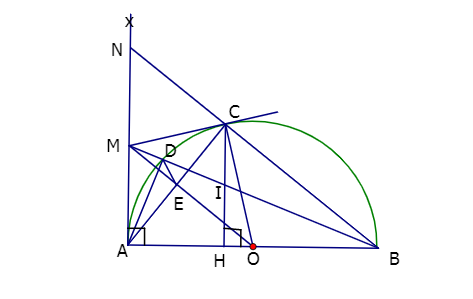
Vì MA, MB, MC là các tiếp tuyến

=>

=> Tứ giác AMCO nội tiếp đường tròn đường kính MO.

Ta có (góc nội tiếp chắn nửa đường tròn)

=>

Ta lại có: OA = OC = R, MA = MC

=> MO là đường trung trực của AC

=>

Từ (*) và (**) => AMDE là tứ giác nội tiếp đường tròn đường kính MA.

Phương pháp 2: Chứng minh tứ giác có hai góc đối diện bù nhau (tổng hai góc đối diện bằng 1800)

Ví dụ: Cho đường tròn (O; R) AB và CD là hai đường kính khác nhau của đường tròn. Tiếp tuyến tại B của đường tròn (O, R) cắt các đường thẳng AC, AD theo thứ tự tại E và F.

a) Chứng minh rằng tứ giác ACBD là hình chữ nhật

b) Chứng minh tam giác ACD và tam giác CBE đồng dạng

c) Chứng minh tứ giác CDEF nội tiếp được đường tròn

Hướng dẫn giải

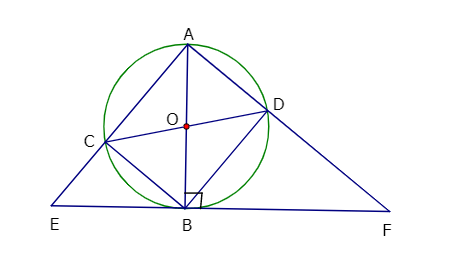
a) Tứ giác ACBD có hai đường chéo AB và CD bằng nhau và cắt nhau tại trung điểm của mỗi đường, suy ra ACBD là hình chữ nhật.

b) Tứ giác ACBD là hình chữ nhật

=> (1)

Ta lại có:

Mà sd BC = sd AD (2)

Từ (1) và (2) =>

c) Vì ACBD là hình chữ nhật nên CB song song với AF

=> (3)

Từ (2) và (3) => do đó tứ giác CDFE nội tiếp được đường tròn.

Phương pháp 3: Chứng minh hai đỉnh cùng nhìn đoạn thẳng tạo bởi hai điểm còn lại hai góc bằng nhau.

Ví dụ: Từ một điểm A nằm bên ngoài đường tròn (O; R) ta vẽ hai tiếp tuyến AB và AC với đường tròn (B, C) là tiếp điểm). Trên cung nhỏ BC lấy điểm M, vẽ MI vuông góc với AB, MK vuông góc với AC (I thuộc AB, K thuộc AC)

a) Chứng minh AIMK là tứ giác nội tiếp đường tròn.

b) Kẻ MP vuông góc BC (P thuộc BC). Chứng minh:

Hướng dẫn giải

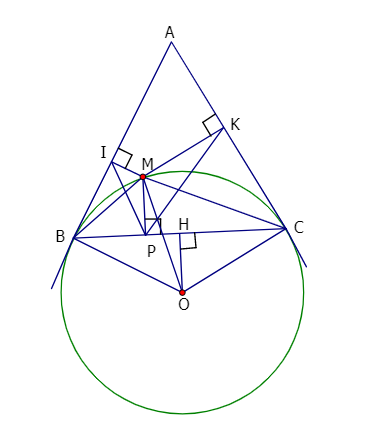
a) Ta có:

=> Tứ giác AIMK nội tiếp đường tròn đường kính AM.

b) Tứ giác CPMK có:

Do đó CPMK là tứ giác nội tiếp

=>

Vì CK là tiếp tuyến của (O) nên ta có:

=>

C. Bài tập chứng minh tứ giác nội tiếp

Bài 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Vẽ AC, AD thứ tự là đường kính của hai đường tròn (O) và (O’).

a) Chứng minh rằng ba điểm C, B, D thẳng hàng.

b) Đường thẳng AC cắt đường tròn (O’) tại E, đường thẳng AD cắt đường tròn (O) tại F (E, F, khác A). Chứng minh bốn điểm C, D, E, F cùng nằm trên một đường tròn.

Bài 2: Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O; R). Các đường cao BE và CF cắt nhau tại H.

Chứng minh rằng tứ giác AEHF và tứ giác BCEF nội tiếp đường tròn.

Bài 3: Cho đường tròn (O) có đường kính AB. Lấy điểm M thuộc đoạn thẳng OA, điểm N thuộc nửa đường tròn (O). Từ A và B vẽ các tiếp tuyến Ax và By. Đường thẳng qua N và vuông góc với MN cắt Ax và By tạo C và D.

a) Chứng minh ACNM và BDNM là các tứ giác nội tiếp đường tròn.

b) Chứng minh Tam giác ANB và tam giác CMD đồng dạng với nhau.

Bài 4: Cho tam giác ABC vuông tại A (AB > AC) đường cao AH. Trên nửa mặt phẳng bờ BC chứa điểm A, vẽ nửa đường tròn đường kính BH cắt AB tại E, nửa đường tròn đường kính HC cắt AC tại F. Chứng minh:

a) Tứ giác AFHE là hình chữ nhật.

b) Tứ giác BEFC là tứ giác nội tiếp đường tròn.

----------------------------------------------

Hy vọng tài liệu Chứng minh tứ giác nội tiếp đường tròn sẽ giúp ích cho các bạn học sinh học nắm chắc kiến thức chuyên đề Đường tròn đồng thời học tốt môn Toán lớp 9. Chúc các bạn học tốt, mời các bạn tham khảo!

Ngoài ra mời quý thầy cô và học sinh tham khảo thêm một số nội dung:

• Luyện tập Toán 9
• Giải bài tập SGK Toán 9
• Đề thi giữa học kì môn Toán 9