CHUYÊN ĐỀ BẤT ĐẲNG THỨC > Bài 9. Bất đẳng Thức AM - GM

×

MathX - Chia sẻ đam mê

Tài khoản của bạn chưa đủ điều kiện để sử dụng phần này. Nếu là thành viên VIP, vui lòng đăng nhập để vào học! Nếu chưa là thành viên VIP, vui lòng liên hệ số 0912698216 hoặc để lại thông tin để được tư vấn và hướng dẫn đăng ký Đóng Cùng chuyên đề

• Bài 1. Phương pháp xét hiệu và biến đổi tương đương
• Bài tập về nhà
• Bài 2. Phương pháp xét hiệu và biến đổi tương đương (tiếp)
• Bài tập về nhà
• Bài 3. Phương pháp xét hiệu và biến đổi tương đương (tiếp theo)
• Bài tập về nhà
• Bài 4. Phương pháp xét hiệu và biến đổi tương đương (tiếp theo)
• Bài tập về nhà
• Bài 5. Phương pháp làm trội
• BTVN: Bài 5. Phương pháp làm trội
• Bài 6. Phương pháp làm trội (tiếp theo)
• BTVN: Bài 6. Phương pháp làm trội (tiếp theo)
• Bài 7. Phương pháp phản chứng
• BTVN: Bài 7. Phương pháp phản chứng
• Bài 8. Phương pháp phản chứng (tiếp theo)
• BTVN: Bài 8. Phương pháp phản chứng (tiếp theo)
• Bài 9. Bất đẳng thức AM - GM
• BTVN: Bài 9. Bất đẳng thức AM - GM

Cùng khóa học

• CHUYÊN ĐỀ HẰNG ĐẲNG THỨC
• CHUYÊN ĐỀ PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
• CHUYÊN ĐỀ ĐƠN THỨC - ĐA THỨC
• CHUYÊN ĐỀ PHÂN THỨC ĐẠI SỐ
• CHUYÊN ĐỀ HÌNH HỌC
• CHUYÊN ĐỀ BẤT ĐẲNG THỨC
• CHUYÊN ĐỀ ĐỒNG DẠNG
• CHUYÊN ĐỀ SỐ HỌC
• CHUYÊN ĐỀ PHƯƠNG TRÌNH NGHIỆM NGUYÊN

Chuyên đề Bài 9. Bất đẳng thức AM - GM TOÁN NÂNG CAO LỚP 8 CHUYÊN ĐỀ BẤT ĐẲNG THỨC Bài 9. Bất đẳng thức AM - GM Cơ bản 5219 lượt học

Ví dụ: Chứng minh rằng:

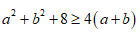
Thảo luận

• 

  Đặng Phương AnhTrả lời

  10:05 16-04-2020

  thầy ơi bài 2 tại sao 8 nhân với căn ab và căn bc và căn ca =8abc ạ ?

  

  Cô Vy MATHX

  18:41 16-04-2020

  Chào em! Em gửi vào phần hỗ trợ học tập để các thầy cô hỗ trợ nhé.

  Trả lời

Gửi ý kiến

Vui lòng đăng nhập để gửi ý kiến ×

Mathx.vn - Ẩn số toán học

Bạn phải đăng nhập để thực hiện chức năng này Close ×

Video bài giảng

... Close ×

Luyện tập bài giảng

Đang lấy dữ liệu... Câu trước Câu sau Nộp bài Đóng ×

MathX

Bạn có chắc là muốn nộp bài? Nộp bài Đóng

Thành viên Đăng nhập Bạn cần đăng nhập để xem đầy đủ các nội dung, hoặc đăng ký ở đây nếu bạn chưa có tài khoản!

Email * Mật khẩu * Ghi nhớ đăng nhập Đăng nhập Đăng nhập với Facebook Đăng nhập với Gmail Quên mật khẩu Đăng ký tài khoản ×

Chọn cấp độ đề thi

Đề dễ Đề nâng cao Đề khó