Công Thức Giải Nhanh Dòng điện Xoay Chiều
Có thể bạn quan tâm
CÔNG THỨC GIẢI NHANH DÒNG ĐIỆN XOAY CHIỀU
I. Đoạn mạch RLC có L thay đổi:
* Khi \(L=\frac{1}{\omega ^{2}C}\) thì IMax Þ URmax; PMax còn ULCMin Lưu ý: L và C mắc liên tiếp nhau
* Khi \(Z_{L}=\frac{R^{2}+{Z_{C}}^{2}}{Z_{C}}\) thì \(U_{Lmax}=\frac{U\sqrt{R^{2}+{Z_{C}}^{2}}}{R}\) và \({U_{Lmax}}^{2}=U^{2}+{U_{R}}^{2}+{U_{C}}^{2};{U_{Lmax}}^{2}=U^{2}-U_{C}.U_{Lmax}-U^{2}=0\)
* Với L = L1 hoặc L = L2 thì UL có cùng giá trị
* Khi \(Z_{L}=\frac{Z_{C}+\sqrt{4R^{2}+{Z_{C}}^{2}}}{2}\) thì \(U_{RLmax}=\frac{2UR}{\sqrt{4R^{2}+{Z_{C}}^{2}-Z_{C}}}\)
Lưu ý: R và L mắc liên tiếp nhau
Lưu ý: R và L mắc liên tiếp nhau
II. Đoạn mạch RLC có C thay đổi:
* Khi \(C=\frac{1}{\omega ^{2}L}\) thì IMax Þ URmax; PMax còn ULCMin
Lưu ý: L và C mắc liên tiếp nhau
* Khi \(Z_{C}=\frac{R^{2}+{Z_{L}}^{2}}{Z_{L}}\) thì \(U_{Cmax}=\frac{U\sqrt{R^{2}+{Z_{L}}^{2}}}{R}\) và \({U_{Cmax}}^{2}=U^{2}+{U_{R}}^{2}+{U_{L}}^{2};{U_{Cmax}}^{2}=U^{2}-U_{L}.U_{Cmax}-U^{2}=0\)
* Khi C = C1 hoặc C = C2 thì UC có cùng giá trị
* Khi \(Z_{C}=\frac{Z_{L}+\sqrt{4R^{2}+{Z_{L}}^{2}}}{2}\) thì \(U_{RCmax}=\frac{2UR}{\sqrt{4R^{2}+{Z_{L}}^{2}-Z_{L}}}\)
Lưu ý: R và C mắc liên tiếp nhau
Thay đổi f có hai giá trị \(f_{1}\neq f_{2}\) biết \(f_{1}+ f_{2}=a\)
III. Bài toán cho ω thay đổi.
- Xác định ω để Pmax, Imax, URmax.
- Khi thay đổi ω, các đại lượng L, C, R không thay đổi nên tương ứng các đại lượng Pmax, Imax, URmax khi xảy ra cộng hưởng: ZL = ZC hay \(\omega =\frac{1}{\sqrt{LC}}\).
- \(\omega L=\frac{1}{C\omega }\Leftrightarrow LC\omega ^{2}=1\Rightarrow \omega\)
- Xác định ω để UCmax. Tính UCmax đó.
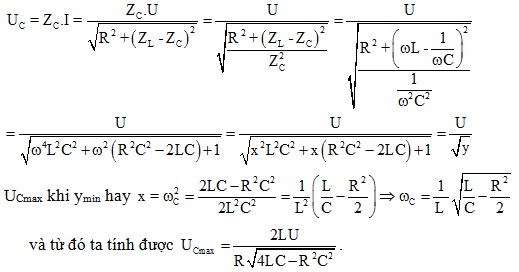
=> Khi \(\omega =\frac{1}{L}\sqrt{\frac{L}{C}-\frac{R^{2}}{2}}\) thì \(U_{Cmax}=\frac{2U.L}{R\sqrt{4LC-R^{2}C^{2}}}\)
- Xác định ω để ULmax. Tính ULmax đó.
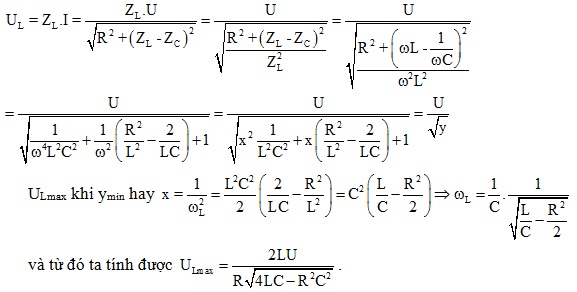
=> Khi \(\omega =\frac{1}{C}\frac{1}{\sqrt{\frac{L}{C}-\frac{R^{2}}{2}}}\) thì \(U_{Lmax}=\frac{2U.L}{R\sqrt{4LC-R^{2}C^{2}}}\)
- Cho ω = ω1, ω = ω2 thì P như nhau. Tính ω để Pmax.

=> Với ω = ω1 hoặc ω = ω2 thì I hoặc P hoặc cosφ hoặc UR có cùng một giá trị
Nghĩa là :Có hai giá trị của để mạch có P, I, Z, cosφ, UR giống nhau thì
\(\omega _{1}\omega _{2}={\omega _{m}}^{2}=\frac{1}{LC}\)
- Cho ω = ω1, ω = ω2 thì UC như nhau. Tính ω để UCmax.
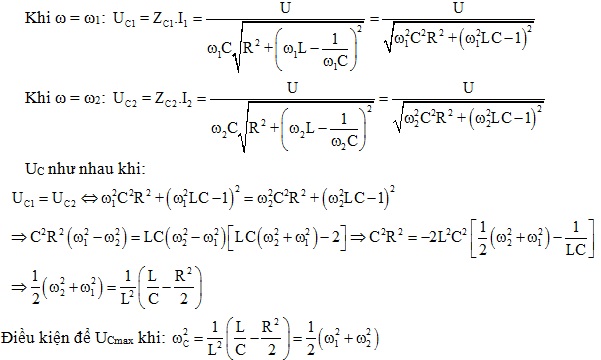
Cho ω = ω1, ω = ω2 thì UL như nhau. Tính ω để ULmax.

Cho ω = ω1 thì ULmax, ω = ω2 thì UCmax. Tính ω để Pmax.
- ULmax khi \(\omega _{1}=\frac{1}{C}.\frac{1}{\sqrt{\frac{L}{C}-\frac{R^{2}}{2}}}\)
- UCmax khi \(\omega _{2}=\frac{1}{L}.\frac{1}{\sqrt{\frac{L}{C}-\frac{R^{2}}{2}}}\)
- Điều kiện để P đạt giá trị cực đại (cộng hưởng) khi:
\(Z_{C}=Z_{L}\Rightarrow \omega ^{2}=\frac{1}{LC}=\omega _{1}\omega _{2}\Rightarrow \omega =\sqrt{\omega _{1}\omega _{2}}\)
IV.CÁC CÔNG THỨC VUÔNG PHA VỀ ĐIỆN XOAY CHIỀU
1 – Đoạn mạch chỉ có L ; uL vuông pha với i
\((\frac{u_{L}}{U_{OL}})^{2}+(\frac{i}{I_{0}})^{2}=1\) với U0L = I0ZL
=>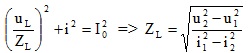
2 – Đoạn mạch chỉ có tụ C ; uC vuông pha với i
\((\frac{u_{C}}{U_{OC}})^{2}+(\frac{i}{I_{0}})^{2}=1\) với U0C = I0ZC => \((\frac{u}{Z_{C}})^{2}+i^{2}={I_{0}}^{2}\)
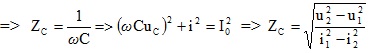
3- Đoạn mạch có LC ; uLC vuông pha với i
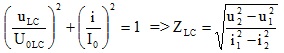
4 – Đoạn mạch có R và L ; uR vuông pha với uL
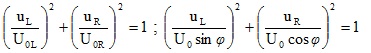
5 – Đoạn mạch có R và C ; uR vuông pha với uC
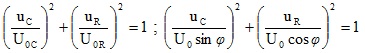
6 – Đoạn mạch có RLC ; uR vuông pha với uLC
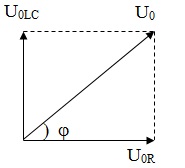
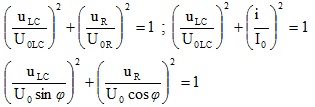
=> U02 = U0R2 + U0LC2
với U0LC = U0R tanφ => \((\frac{u_{LC}}{tan\varphi })^{2}+{u_{R}}^{2}={U_{0R}}^{2}\)
7 – Từ điều kiện để có hiện tượng cộng hưởng ω02LC = 1
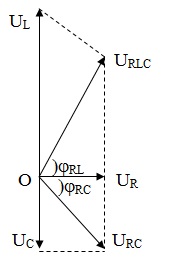
Xét với ω thay đổi
7a : 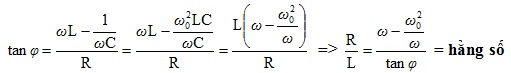
7b : ZL =ωL và \(Z_{C}=\frac{1}{\omega C}\)
![]()
=> đoạn mạch có tính cảm kháng ZL > ZC => ωL > ω0
=> đoạn mạch có tính dung kháng ZL < ZC => ωC < ω0
=> khi cộng hưởng ZL = ZC => ω =ω0
7c : I1 = I2 < Imax => ω1 ω 2 = ω 02 Nhân thêm hai vế LC
=> ω 1ω 2LC = ω 02LC = 1
=> ZL1 = ω1L và ZC2 = 1/ ω2C
=> ZL1 = ZC2 và ZL2 = ZC1
7d : Cosφ1 = cosφ2 => ω1ω 2LC = 1 thêm điều kiện L = CR2
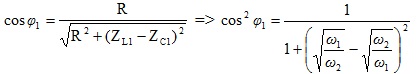
8 – Khi L thay đổi ; điện áp hai đầu cuộn cảm thuần L => URC ⊥ URLC => từ GĐVT
ULmax <=> tanφRC. tanφRLC = – 1
=>\(Z_{L}=\frac{R^{2}+{Z_{C}}^{2}}{Z_{C}}\) => ZL2 = Z2 + ZCZL
=> \(U_{Lmax}=\frac{U}{R}\sqrt{R^{2}+{Z_{C}}^{2}}\) và \(U_{Lmax}=\frac{{U_{R}}^{2}+{U_{C}}^{2}}{U_{C}}\)
=> U2Lmax = U2 + U2R + U2C
=> \({U_{Lmax}}^{2}=U^{2}+U_{C}U_{Lmax}\)
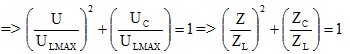
9 – Khi C thay đổi ; điện áp hai đầu tụ C => URL ⊥ URLC
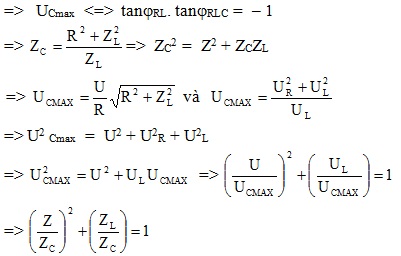
10 – Khi URL^ URC
=> ZLZC = R2 => \(U_{R}=\frac{U_{RL}U_{RC}}{\sqrt{{U_{RL}}^{2}+{U_{RC}}^{2}}}\) => tanφRL. tanφRC = – 1
11 – Điện áp cực đại ở hai đầu tụ điện C khi ω thay đổi
Với ωC = \(\sqrt{\frac{2\frac{L}{C}-R^{2}}{2L^{2}}}\) (1) => ω2 = ωC2 = ω02 – \(\frac{R^{2}}{2L^{2}}\) (2)
=> cách viết kiểu (2) mới dễ nhớ hơn (1)
với ZL = ωCL và ZC = 1/ ωCC => \(\frac{Z_{L}}{Z_{C}}={\omega _{C}}^{2}LC=\frac{{\omega _{C}}^{2}}{{\omega _{0}}^{2}}\)
=> từ \(U_{Cmax}=\frac{2LU}{R\sqrt{4LC-R^{2}C^{2}}}\) (3)
=> từ (2) và (3) suy dạng công thức mới
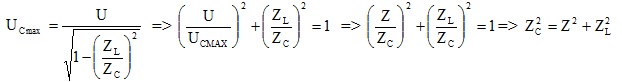
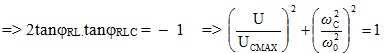
12 – Điện áp ở đầu cuộn dây thuần cảm L cực đại khi w thay đổi
Từ \(\omega =\sqrt{\frac{2}{2LC-R^{2}C^{2}}}\) (1) => \(\frac{1}{{\omega _{L}}^{2}}=\frac{1}{{\omega _{0}}^{2}}-\frac{R^{2}C^{2}}{2}\) (2)
=> cách viết kiểu (2) mới dễ nhớ hơn (1)
; ZL = ωLL và ZC = 1/ωLC => \(\frac{Z_{C}}{Z_{L}}=\frac{1}{{\omega _{L}}^{2}LC}=\frac{{\omega _{0}}^{2}}{{\omega _{L}}^{2}}\)
Từ \(U_{Lmax}=\frac{2LU}{R\sqrt{4LC-R^{2}C^{2}}}\) (3) = > dạng công thức mới
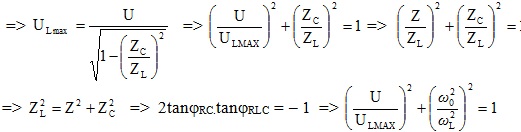
13 – Máy phát điện xoay chiều một pha
Từ thông \(\Phi =\Phi _{0}cos(\omega t+\varphi )\)
Suất điện động cảm ứng \(2=-\frac{d\Phi }{dt}\) \(\omega \Phi _{0}sin(\omega t+\varphi )\)= E0sin (ωt + φ )
\((\frac{\Phi }{\Phi _{0}})^{2}+(\frac{e}{E_{0}})^{2}=1\)
Phần chứng minh các công thức 11; 12
CÔNG THỨC HAY :
Trong đoạn mạch xoay chiều , RLC ( cuộn dây thuần cảm ) với điện áp hai đầu đoạn mạch U = không đổi . Xét trường hợp w thay đổi .
Các bạn đều biết
1 – Xét điện áp cực đại ở hai đầu điện trở R
![]()
2- Xét điện áp cực đại ở hai đầu tụ điện C

Công thức (*) các tài liệu tham khảo đều viết như vậy, nhưng chỉ biến đổi một chút xíu thôi là có công thức dễ nhớ hơn và liên hệ hay như sau
Bình phương hai vế và rút gọn L . Ta có
![]()
=> Vậy là giữa (1b) và (2b) có liên hệ đẹp rồi .
Từ (2a ) chia tử mẫu cho 2L và đưa vào căn => ( 2b) thay vào (2a) trong căn , ta có
\(U_{Cmax}=\frac{U}{\sqrt{1-(\frac{Z_{L}}{Z_{C}})^{2}}}\)
(2c) để tồn tại đương nhiên ZC > ZL và không có R
3 – Xét điện áp cực đại ở hai đầu cuộn dây thuần cảm L
ULmax = \(\frac{2LU}{R\sqrt{4LC-R^{2}C^{2}}}\) (3a) Khi \(\omega =\sqrt{\frac{2}{2LC-R^{2}C^{2}}}\) ( ** )
Công thức ( ** ) các tài liệu tham khảo cũng hay viết như vậy. Tương tự như trên bình phương hai vế và viết nghịch đảo
![]()
Giữa (3b) và (1b) lại có liên hệ nữa rồi .Tương tự dùng (3b) thay (3a) ta có
\(U_{Lmax}=\frac{U}{\sqrt{1-(\frac{Z_{C}}{Z_{L}})^{2}}}\)
(3c) để tồn tại đương nhiên ZL > ZCvà không có R
4 – Kết hợp (1b) , (2b) , (3b) Ta có : \(\omega _{C}\omega _{L}={\omega _{R}}^{2}\)= ω02
5- Chứng minh khi UCmax với ω thay đổi thì:
2tanφRL.tanφRLC = – 1
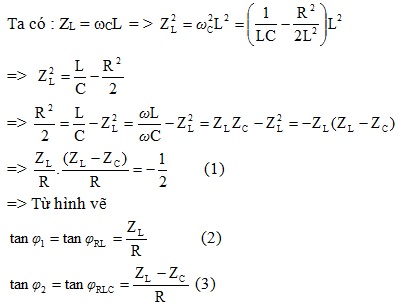
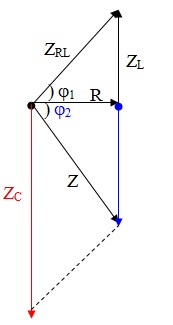
=> Từ 1,2,3 : 2tanφRL.tanφRLC = – 1
à Lưu ý là có số 2 ở phía trước nhé, nên trường hợp này URL không vuông góc với URLC .
Phần khi ULmax chứng tương tự
5– Khi ω thay đổi với ω = ωC thì UCmax và ω = ωL thì ULmax nhưng nếu viết theo biểu thức dạng 2a và 3a thì : UCmax = ULmax cùng một dạng, nhưng điều kiện có nghiệm là ω = ωC ≠ ω = ωL
Nhưng nếu viết dạng (2c) và (3c) thì lại khác nhau .
Cả hai cách viết dạng a hay c của UmaxC hay UmaxL đều rất dễ nhớ .
6 – Khi các giá trị điện áp cực đại UmaxR ; UmaxC ; Umax L với các tần số tương ứng
ωR ; ωC ; ωL thì có một mối quan hệ cũng rất đặc biệt đó là
ωL > ωR > ωC => điều này dễ dàng từ các biểu thức 2b và 3b
Nhận xét : Có thể nói còn rất nhiều hệ quả hay vận dụng từ hai dao động có pha vuông góc hoặc từ con số 1 ở vế phải . Ta có thể dùng để giải nhiều bài toán nhanh và dễ nhớ !
Từ khóa » Tính I Trong Mạch Rlc
-
Tóm Tắt Công Thức Giải Nhanh Vật Lý 12: 3 Dạng Bài Tập Dòng ...
-
Tổng Hợp Các Công Thức Vật Lý 12 Quan Trọng Dòng Điện Xoay ...
-
Các đại Lượng U, I Của Mạch điện RLC - Baitap123
-
[Chi Tiết] Công Thức Mạch RLC Nối Tiếp Và Cộng Hưởng Điện
-
Mạch điện Xoay Chiều R, L, C Mắc Nối Tiếp, Hiện Tượng Cộng Hưởng ...
-
Mạch điện RLC – Wikipedia Tiếng Việt
-
Lý Thuyết Mạch điện Xoay Chiều R L C Mắc Nối Tiếp Hay đầy đủ Nhất
-
Công Thức Tính Nhanh điện Xoay Chiều - SlideShare
-
Công Thức Mạch RLC Vật Lý 12 - 123doc
-
Bài Toán Ngược Xác định RLC
-
Bài Tập Vật Lý Lớp 12 Viết Biểu Thức U Và I Trong Mạch điện Xoay Chiều.
-
Cách Tính Tổng Trở Của đoạn Mạch RLC Mắc Nối Tiếp Hay, Chi Tiết
-
Zl Là Gì Trong Vật Lý 12: 3 Dạng Bài Tập Dòng Điện Xoay Chiều ...