Công Thức Tính Diện Tích Hình Thang Và Bài Tập ứng Dụng - Cunghocvui
Có thể bạn quan tâm
Công thức tính diện tích hình thang và bài tập ứng dụng
Công thức tính diện tích hình thang cũng như các công thức tính diện tích tam giác, khá đơn giản và gần như đã trở thành một công thức phổ thông được nhiều học sinh, sinh viên áp dụng để giải quyết các bài toán cơ bản trong môn toán học. Tuy nhiên trong nhiều trường hợp, không phải ai cũng hiểu và biết cách tính diện tích hình thang đúng cũng như cách áp dụng vào thực tế. Chúng tôi sẽ giúp bạn giải đáp thắc mắc này!
I. Định nghĩa hình thang
1. Hình thang là gì?
Hình thang là tứ giác lồi có hai cạnh đáy song song.
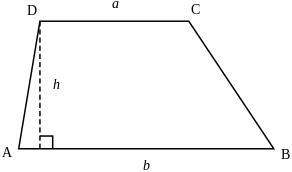
2. Dấu hiệu nhận biết hình thang
Hình thang vuông:
- Hình thang có một góc vuông là hình thang vuông.
Hình thang cân:
- Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân.
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
- Hình thang có hai trục đối xứng của hai đáy trùng nhau là hình thang cân.
- Hình thang có hai cạnh bên bằng nhau (nếu hai cạnh bên ấy không song song) là hình thang cân.
II. Các công thức liên quan
1. Công thức tính chu vi hình thang
Chu vi hình thang bằng tổng độ dài của hai đáy và hai cạnh bên (tất cả các cạnh của nó):
\(P=a+b+c+d\)
Ví dụ: Cho hình thang ABCD như hình 1, trong đó cạnh đáy lớn AB=15 cm, cạnh đáy bé CD=13 cm, cạnh bên AD= 3 cm, BC = 5 cm. Hãy tính chu vi hình thang ABCD.
Áp dụng công thức tính chu vi hình thang ta có P= AB + BC + CD + DA
=> P = 15 + 13 + 3 + 5 = 36 cm.
2. Công thức tính diện tích hình thang
Diện tích của hình thang bằng chiều cao nhân với trung bình cộng của hai cạnh đáy:
\(S=h\times(\dfrac {a+b}{2})\)
Diện tích của hình thang bằng đường trung bình nhân với chiều cao hình thang.
- Áp dụng công thức tính diện tích hình thang cân:
Cho hình thang cân ABCD, trong đó ta có:
AB // CD và góc C = góc D, hai cạnh bên AD= BC. Kẻ đường cao AH vuông góc với DC, BK vuông góc với DC.
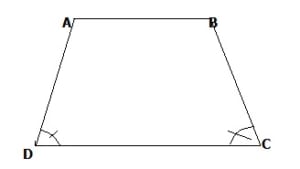
\(\rightarrow S _{ABCD} = S_{ AHD} + S_ {BKC} + S_{ AHKB}.\)
Mà diện tích tam giác AHD = Diện tích tam giác BKC do có cùng độ dài đáy và chiều cao \(\rightarrow S _{ABCD} = 2S_{ AHD} + S_{ AHKB}.\)
\(\rightarrow S_{ABCD}=2\times (\dfrac{1}{2}×AH×DH) + (AB×AH).\)
- Áp dụng công thức tính diện tích hình thang vuông:
Cho hình thang vuông ABCD (Hình 1 ), trong đó h= AD (h:ký hiệu chiều cao )
Vậy Diện tích hình thang vuông ABCD là: \(S= \dfrac{AB+CD}{2} × AD\)
Xem ngay tại: Công thức tính diện tích, đường trung bình của hình thang
III. Bài toán liên quan đến công thức tính diện tích hình thang lớp 8
Bài tập mẫu có lời giải
Bài 1: Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB//CD)(AB//CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng mình rằng:
a) ∆BDE là tam giác cân.
b) ∆ACD = ∆BDC.
c) Hình thang ABCD là hình thang cân.
Lời giải:
a) E thuộc đường thẳng DC nên CE // AB.
Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song (gt) nên \(⇒AC=BE⇒AC=BE\) (1) (tính chất hình thang )
Lại có: AC = BD (gt) (2)
Từ (1) và (2) suy ra \(BE = BD ⇒ΔBED\) cân tại B (dấu hiệu nhận biết tam giác cân).
b) Ta có \(AC//BE⇒\widehat{C_1}=\widehat{E}\) (2 góc đồng vị) (3)
∆BDE cân tại B (cmt) \( ⇒\widehat {D_1}=\widehat{E}\) (4)
Từ (3) và (4) \(⇒\widehat {D_1}=\widehat{C_1}\)
Xét ∆ACD và ∆BCD có:
AC = BD (gt)
\(\widehat {D_1}=\widehat{C_1}\) (cmt)
CD chung
Nên ∆ACD = ∆BDC (c.g.c)
c) Ta có: ∆ACD = ∆BDC (cmt)
\(⇒\widehat{ADC}=\widehat{BCD}\) (2 góc tương ứng)
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Hot: Ứng dụng tích phân để tính diện tích hình thang
Bài 2: Ta có hình thang ABCD với các cạnh AB = 8, cạnh đáy CD = 13, chiều cao giữa 2 cạnh đáy là 7 thì chúng ta sẽ có phép tính diện tích hình thang là:
\(S_{ABCD} = 7 \times \dfrac{8+13}{2} = 73.5\)
Luyện tập
Bài 1: Tính diện tích hình thang có đáy lớn 54 m; đáy bé bằng \(\dfrac{2}{3}\) đáy lớn và bằng \(\dfrac{3}{2}\) chiều cao.
Bài 2: Tính diện tích hình thang có đáy lớn bằng 25 m, chiều cao bằng 80% đáy lớn, đáy bé bằng 90% chiều cao.
Bài 3: Tính diện tích hình thang có đáy bé bằng 40 cm, chiều cao bằng 30% đáy bé và bằng 20% đáy lớn.
Bài 4: Tính diện tích hình thang có đáy lớn bằng 50 dm và bằng 80% chiều cao, đáy bé kém đáy lớn 12 dm.
Bài 5: Tính diện tích hình thang có chiều cao bằng 4 dm, đáy bé bằng 80% chiều cao và kém đáy lớn 1,2 dm.
Bài 6: Hình thang có tổng độ dài hai đáy bằng 24 cm, đáy lớn hơn đáy bé 1,2 cm, chiều cao kém đáy bé 2,4 cm. Tính diện tích hình thang.
Bài 7: Hình thang có đáy lớn hơn đáy bé 20,4 dm và bằng 3 5 đáy bé, chiều cao hơn đáy bé 2,1 dm. Tính diện tích hình thang.
Bài 8: Hình thang có tổng độ dài hai đáy bằng 14,5dm, đáy lớn gấp rưỡi đáy bé, chiều cao kém đáy bé 2,8 dm. Tính diện tích hình thang.
Bài 9: Hình thang có tổng độ dài hai đáy bằng 30,5 dm, đáy lớn bằng 1,5 lần đáy bé, chiều cao hơn đáy bé 6,2 dm. Tính diện tích hình thang.
Xem thêm:
- Bài tập về dien tich hinh thang
- Bài 2 trang 94 (Diện tích hình thang) SGK Toán 5
- Bài 18 trang 75 SGK Toán 8 tập 1
Trên đây là bản tổng hợp các bài tập về công thức tính diện tích hình thang cần ghi nhớ, nếu bạn quan tâm thì hãy lưu lại mỗi khi cần thiết nhé. Hy vọng rằng những thông tin chúng tôi cung cấp sẽ giúp bạn tìm ra được phương pháp làm tốt nhất cho dạng bài tập này. Chúc bạn đạt được điểm số cao!
Tags Diện tích hình thang hình thang chu vi hình thangTừ khóa » Cách Tính Diện Tích Hình Thang Lớp 8
-
Công Thức Tính Diện Tích Hình Thang: Thường, Vuông, Cân
-
Diện Tích Hình Thang - Chuyên đề Môn Toán Lớp 8
-
Lý Thuyết Diện Tích Hình Thang | SGK Toán Lớp 8
-
Công Thức Tính Diện Tích Hình Thang - THPT Sóc Trăng
-
Hình Học Lớp 8 Diện Tích Hình Thang Ngắn Gọn Và Chi Tiết Nhất
-
Toán Lớp 8 - 6.4. Diện Tích Hình Thang - Học Thật Tốt
-
Giải Toán 8 Bài 4: Diện Tích Hình Thang
-
Bài Tập Về Diện Tích Hình Thang Lớp 8 - Thủ Thuật
-
Cách Tính Diện Tích Hình Thang - Giải Bài Tập Toán Lớp 8 - GiaiNgo
-
Công Thức Tính Diện Tích Hình Thang, Hinh Thang Cân, đường Chéo ...
-
Công Thức Cách Tính Diện Tích Hình Thang Lớp 8 | Toán Lớp 8 - YouTube
-
Công Thức Tính Diện Tích Hình Thang, Chu Vi Hình Thang Chính Xác 100%
-
Lý Thuyết Toán 8: Bài 4. Diện Tích Hình Thang - TopLoigiai
-
Luyện Tập Diện Tích Hình Thang (có đáp án)