Luyện Tập Diện Tích Hình Thang (có đáp án)

  LUYỆN TẬP DIỆN TÍCH HÌNH THANG

(CÓ ĐÁP ÁN)

A. LÝ THUYẾT

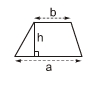
Công thức tính diện tích hình thang: Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.

S  = 1/2 (a+b).h

 

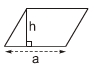
Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.

S = ah

B. BÀI TẬP

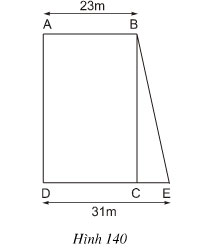
Bài 1. Tính diện tích hình thang ABED theo các độ dài đã cho trên hình 140 và biết diện tích hình chữ nhật ABCD là 828 m2

 

Giải: 

Ta có SABCD = AB. AD = 828 m2

Nêm AD = 828/23 = 36 (m)

SABED=  (AB + DE).AD / 2 = (23 + 31).36 /2 = 972(m2)

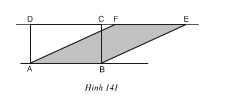
Bài 2: Vì sao hình chữ nhật ABCD và hình bình hành ABEF (h.141) lại có cùng diện tích ? Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước.

 

Lời giải:

Hình chữ nhật ABCD và hình bình hành ABEF có đáy chung là AB và có chiều cao bằng nhau, vậy chúng có diện tích bằng nhau.

Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước:

– Lấy nột cạnh của hình bình hành ABEF làm một cạnh của hình chữ nhật cần vẽ, chẳng hạn cạnh AB.

– Vẽ đường thẳng EF.

– Từ A và b vẽ các đường thẳng vuông góc với đường thẳng EF, chúng cắt đường thẳng EF lần lượt tại D, C. vẽ các đoạn thẳng AD, BC. ABCD là hình chữ nhật có cùng diện.tích với hình bình hành ABEF đã cho.

 Bài 3. Xem hình 142 (IG// FU). Hãy đọc tên một số hình có cùng diện.tích với hình.bình.hành FIGE.

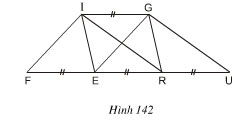
Lời giải

Ta có IG // FU nên khoảng cách giữa hai đường thẳng IG và FU không đổi và bằng h. Các hình.bình.hành FIGE, IGRE, IGUR có cạnh bằng nhau FE = ER = RU có cùng chiều cao ứng với cạnh đó nên diện.tích chúng bằng nhau. Tức là SFIGR = SIGRE = SIGUR( = h. FE)

Mặt khác các tam giác IFG, GEU có cạnh đáy FR và EU bằng nhau, bằng hai lần cạnh hình.bìnhhành FIGE nên diện tích chúng bằng nhau:

SIFR = SGEU = SFIGE

Vậy SFIGE = SIGRE = SIGUR = SIFR = SGEU

Bài 4. Khi nối trung điểm của hai đáy hình thang, tại sao ta được hai hình thang có diện tích bằng nhau?

 

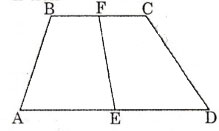
Lời giải:

Cho hình thang ABCD, gọi E,F lần lượt là trung điểm của hai đáy AD, BC. Gọi h là độ dài đường cao của ABCD.

Ta có: SABFE = ½. (AE+BF).h = ½.(ED+FC).h

= SCDEF (Vì AE = ED, BF = FC)

Vậy SABFE = SCDEF.

 

Bài 5. Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh  dện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang.

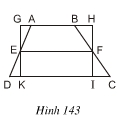
Giải: 

Vì EF là đường trung bình của hình thang ABCD nên EF = 1/2(AB +CD)

Khi đó SABCD =1/2.(AB+CD).GK = EF.GK = GH.GK =SGHIK

* Ta có thể chứng minh công thức tính S.hình thang ABCD bằng cách dựng hình chữ nhật GHIK như trong hình vẽ (Có một cạnh bằng chiều cao và một cạnh bằng đường trung bình của hình thang).

Ta có ΔDEK = ΔAEG và ΔCIF = ΔBHF (Cạnh góc vuông – góc nhọn)

⇒ S DEK = SAEG, SCIF=SBHF.

Khi đó SABCD = SDEK+ SEABF + SEFIK + SCIF = SAEG + SEABF + SEFIK + SBHF

= SGHIK = GH.GK = EF.GK = ½. (AB +CD).GK

Bài 6. Xem hình 144. Hãy chỉ ra các hình có cùng diệntích (lấy ô vuông làm đơn vị diện tích)

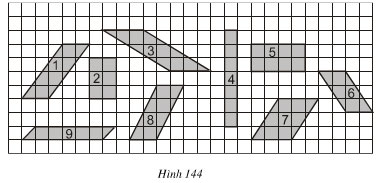
Lời giải:

Các hình 2,6,9 có cùng diện tích là 6 ô vuông.

Các hình 1, 5, 8 có cùng diện tích là 8 ô vuông.

Các hình 3,7  có cùng diện tích là 8 ô vuông.

Hình 4 có diện tích là 7 ô vuông nên không có diện tích với một trong các hình đã cho.

Bài 7. Tìm x, biết đa giác ở hình vẽ có diện tích bằng 3375 m2

 

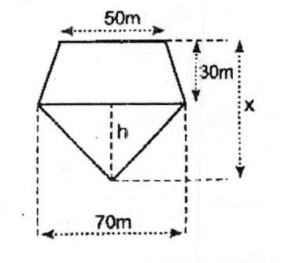
Lời giải:

Hình đa giác đã cho gồm một hình thang và một hình tam giác.

Diện tích phần hình thang là S1, tam giác là S2, ta có:

S1 = (50 + 70) / 2 .30 = 1800 (m2)

S2 = S - S1 = 3375 - 1800 = 1575 (m2)

Chiều cao h của tam giác là: h = (2.S2) / 70 = (2.1575) / 70 = 45 (m)

Vậy x = 45 + 30 = 75 (m)

 Bài 8. Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC = 3cm. Vẽ hình bình hành ABEF có cạnh AB = 5cm và diện tích bằng diện tích hình chữ nhật. Vẽ được bao nhiêu hình như vậy?

Lời giải:

 

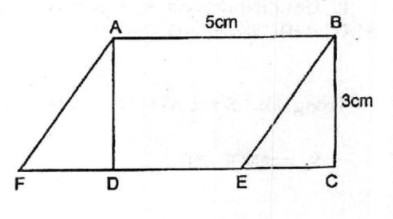
Trên cạnh CD ta lấy 1 điểm E bất kỳ (E khác C và D). Nối BE. Từ A kẻ đường thẳng song song với BE cắt đường thẳng CD tạị F. Ta có hình bình hành ABEF có cạnh AB và có diện tích bằng diện tích hình chữ nhật.

Ta có: SABCD = AB.AD

SABEF = AB.AD ⇒ SABCD = SABEF

Có thể vẽ được vô số hình như vậy.

Bài 9.

Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC=3cm. Vẽ hình bình hành ABEF có cạnh AB = 5cm, BE = 5cm và có diện tích bằng diện tích của hình chữ nhật ABCD. Vẽ được mấy hình như vậy?

Lời giải:

 

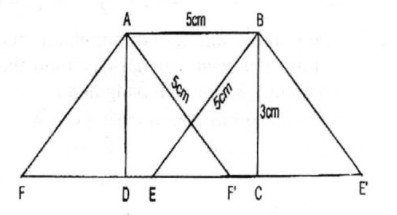
Vẽ cung tròn tâm B bán kính 5cm cắt CD tại 2 điểm E và E'.

Nối BE, từ A kẻ đường thẳng song song với BE cắt CD tại F.

Nối BE', từ A kẻ đường thẳng song song với BE' cắt CD tại F'.

Ta có hình bình hành ABEF và hình bình hành ABE'F' có cạnh AB = 5cm, BE = 5cm, BE' = 5cm có diện tích bằng điện tích hình chữ nhật ABCD.

Có thể vẽ được hai hình như vậy.

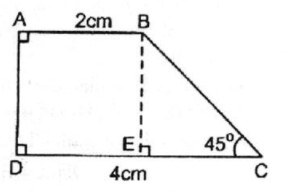Bài 10.  Tính diện tích hình thang vuông, biết hai đáy có độ dài là 2cm, 4cm, góc tạo bởi một cạnh bên và đáy lớn có số đo bằng 45o.

Lời giải:

 

Giả sử hình thang vuông ABCD có:

∠A = ∠D = 90o; ∠C = 45o

Kẻ BE ⊥ CD

Tam giác vuông BEC có ∠(BEC) = 90o cân tại E ⇒ BE = EC

Hình thang ABCD có hai cạnh bên AD // BE (vì cùng vuông góc với DC) ⇒ DE = AB = 2cm

EC = DC – DE = 4 – 2 = 2 (cm) ⇒ BE = 2cm

SABCD = 1/2.BE(AB+ CD) = 1/2.2.(2 + 4) = 6 (cm2)

Bài 11. Tính diện tích hình thang, biết các dây có độ dài là 7cm và 9cm, một trong các cạnh bên dài 8cm và tạo với đây một góc có số đo bằng 30o

Lời giải:

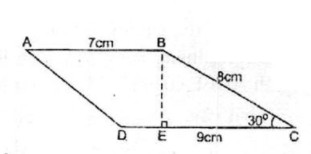
Giả sử hình thang ABCD có đáy AB = 7Cm và CD = 9cm , cạnh bên BC = 8cm, C = 30o

Kẻ BE ⊥ CD. Tam giác vuông GBE có ∠E = 90o, ∠C = 30o

Suy ra ∠(CBE) = 60o nên nó là một nửa tam giác đều có cạnh là CB.

⇒ BE = ½. CB = 4 (cm)

Vậy SABCD = (AB + CD) / 2 .BE = (7 + 9)/2.4 = 32 (cm2)

Bài 12. Chứng minh rằng mọi đường thẳng đi qua trung điểm của đường trung bình của hình thang và cắt hai dây hình thang sẽ chia hình thang đó thành hai hình thang có diện tích bằng nhau.

Lời giải:

  

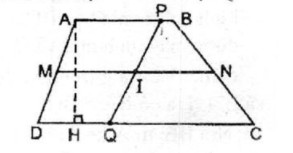
Giả sử hình thang ABCD có AB // CD, đường trung bình là MN. Gọi I là trung điểm của MN, đường thẳng bất kỳ đi qua I cắt AB tại P và CD tại Q.

Ta có hai hình thang APQD và BPQC có cùng đường cao.

MI là đường trung bình của hình thang APQD.

Suy ra: MI = 1/2 (AP + QD)

IN là đường trung bình của hình thang BPQC.

Suy ra: IN = 1/2 (BP + QC)

SAPQD = 1/2 (AP + QD).AH = MI.AH (1)

SBPQC = 1/2 (BP + QC).AH = IN.AH (2).

IM = IN (gt) (3)

Từ (1), (2) và (3) suy ra: SAPQD = SBPQC, các giá trị này không phụ thuộc vào vị trí của P và Q.

Bài 13.  Một hình chữ nhật có các kích thước a và b. Một hình bình hành cũng có hai cạnh là a và b. Tính góc nhọn của hình bình hành nếu diện tích của nó bằng một nửa diện tích hình chữ nhật (a và b có cùng đơn vị đo).

Lời giải:

 

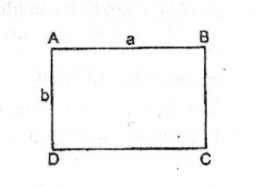
* Xét hình chữ nhật ABCD có chiều dài AB = a, chiều rộng AD = b.

Ta có: SABCD = ab.

* Hình bình hành MNPQ có góc M là góc tù, MN = a, cạnh MQ = b

Kẻ đường cao MH. Ta có: SMNPQ = MH.a

Theo bài ra, ta có: MH.a = 1/2 ab

Suy ra: MH = 1/2 b hay MH = MQ/2

Tam giác MHQ vuông tại H và MH = MQ/2

Cạnh đối diện góc nhọn bằng một nửa cạnh huyền nên ∠(MQH) = 30o

Vậy góc nhọn của hình bình hành bằng 30o.

Bài 14. Hai cạnh của một hình hình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp số.

Lời giải:

 

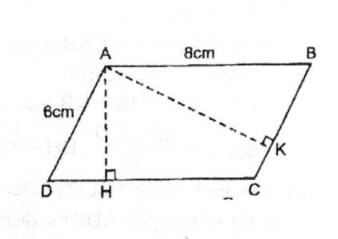
Giả sử hình bình hành ABCD cói AB = 8cm, AD = 6cm.

Kẻ AH ⊥ CD, AK ⊥ BC. Ta có 5 < 6, 5 < 8

Đường cao là cạnh góc vuông nhỏ hơn cạnh huyền thỏa mãn có hai trường hợp:

*Trường hợp 1: AK = 5cm

Ta có: SABCD = AK.BC = 5.6 = 30 (cm2)

SABCD = AH.AD = 8.AH

Suy ra: 8.AH = 30 ⇒ AH = 30/8 = 15/4 (cm)

*Trường hợp 2: AH = 5cm

Ta có: SABCD = AH.CD= 5.8 = 40 (cm2)

SABCD = AK.BC = 6.AH

Suy ra: 6.AK = 40 ⇒ AK = 40/6 = 20/3 (cm)

Vậy đường cao thứ hai có độ dài là 15/4 cm hoặc 20/3 cm

Bài toán có hai đáp số.