Đề Thi Đại Học Môn Toán Khối A Năm 2010
Click vào đề thi
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = x3 – 2x2 + (1 – m)x + m (1), m là số thực Khảo sát sự biến thiên và vẽ đồ thị hàm sô khi m = 1 Tìm m để đồ thị của hầm số (1) cắt trục hoành tại 3 điểm phân biệt có hoành độ x1 , x2 , x3 thỏa mãn điều kiện x12 + x22 + x32 < 4
Câu 2: Giải phương trình: 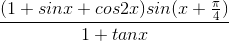 = cosx
= cosx
Câu 3: Giải bất phương trình: 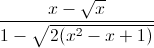 ≥ 1
≥ 1
Câu 4: Tính tích phân: I = 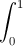
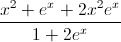 dx
dx
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH = a√3 . Tính thể tích khối chóp S.CDNM và khoảng cách giữa hai đường thẳng DM và SC theo a.
Câu 6: Giải hệ phương trình: 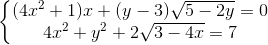 (x , y ∈
(x , y ∈ 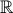 )
)
Câu 7: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d1: 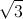 x + y = 0 và d2:
x + y = 0 và d2: 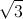 x – y = 0. Gọi (T) là đường tròn tiếp xúc với d1 tại A, cắt d2 tại hai điểm B và C sao cho tam giác ABC vuông tại B. Viết phương trình của (T), biết tam giác ABC có diện tích bằng
x – y = 0. Gọi (T) là đường tròn tiếp xúc với d1 tại A, cắt d2 tại hai điểm B và C sao cho tam giác ABC vuông tại B. Viết phương trình của (T), biết tam giác ABC có diện tích bằng 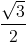 và điểm A có hoành độ dương.
và điểm A có hoành độ dương.
Câu 8: Trong không gian tọa độ Oxyz, cho đường thẳng ∆: 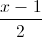 =
= 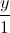 =
= 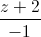 và mặt phẳng (P): x - 2y + z = 0. Gọi C là giao điểm của ∆ với (P). M là điểm thuộc ∆. Tính khoảng cách từ M đến (P), biết MC = √6
và mặt phẳng (P): x - 2y + z = 0. Gọi C là giao điểm của ∆ với (P). M là điểm thuộc ∆. Tính khoảng cách từ M đến (P), biết MC = √6
Câu 9: Tìm phần ảo của số phức z, biết  = (
= (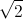 + i)2 (1 -
+ i)2 (1 - 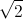 i)
i)
Câu 10: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại A có đỉnh A(6 ; 6), đường thẳng đi qua trung điểm của các cạnh AB và AC cso phương trình x + y - 4 = 0. Tìm tọa độ các đỉnh B và C, biết điểm E(1 ; -3) nằm trên đường cao đi qua đỉnh C của tam giác đã cho.
Câu 11: Trong không gian tọa độ Oxyz, cho điểm A(0 ; 0 ; -2) và đường thẳng ∆: 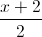 =
= 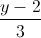 =
= 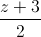 Tính khoảng cách từ A đến ∆ . Viết phương trình mặt cầu tâm A, cắt ∆ tại hai điểm B và C sao cho BC = 8
Tính khoảng cách từ A đến ∆ . Viết phương trình mặt cầu tâm A, cắt ∆ tại hai điểm B và C sao cho BC = 8
Câu 12: Cho số phức z thỏa mãn 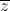 =
= 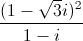 . Tìm modun của số phức
. Tìm modun của số phức 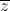 + iz
+ iz
Từ khóa » Toán Khối A 2010
-
Đề Thi đại Học Môn TOÁN Khối A Năm 2010 ❤️✔️
-
Đề Thi Và đáp án Môn Toán Khối A Năm 2010
-
Đáp án Chính Thức Môn Toán - Khối A - Kỳ Thi Đại Học Năm 2010
-
[Top Bình Chọn] - đề Toán Khối A Năm 2010 - Trần Gia Hưng
-
Đề Thi Thử đại Học Năm 2010 Môn Toán - Khối A
-
ĐỀ THI ĐẠI HỌC MÔN TOÁN KHỐI A NĂM 2010 - 123doc
-
Đề Thi & Đáp án Tuyển Sinh Đại Học – Cao đẳng Năm 2010
-
Đáp án Môn Toán, Khối A Kỳ Thi ĐH Năm 2010 - Vật Lý 360 độ
-
Đề Thi Tuyển Sinh Cao đẳng Năm 2010 Môn Thi: Toán, Khối A
-
Giải đề Thi ĐH Năm 2010 Môn Toán Khối A
-
Gợi ý Giải đề Thi Môn Toán, Khối A Năm 2010 - PLO