Diện Tích Toàn Phần Hình Trụ Tròn Xoay Là Gì ? Cách Tính Kèm Ví Dụ ...

Home » Toán Học » Diện tích toàn phần hình trụ tròn xoay là gì ? Cách tính kèm ví dụ minh họa Toán Học Diện tích toàn phần hình trụ tròn xoay là gì ? Cách tính kèm ví dụ minh họa admin.ta 15 Tháng Tám, 2021 36 Views 0 SaveSavedRemoved 0

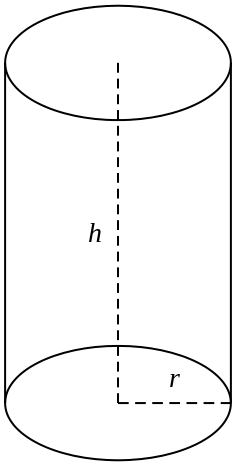
Diện tích toàn phần hình trụ tròn xoay được tính khi khi bạn xác định được những yếu tố nào ? Cùng chúng tôi đi tìm câu trả lời ngay trong bài viết dưới đây nhé !

Tham khảo bài viết khác: 

• Công thức tính diện tích toàn phần của hình nón
• Thể tích hình lập phương là gì ? Thể tích hình lập phương khi biết đường chéo ?

   Công thức tính diện tích toàn phần hình trụ tròn xoay

Tóm tắt nội dung

• 1    Công thức tính diện tích toàn phần hình trụ tròn xoay
• 2     Ví dụ minh họa cách tính diện tích toàn phần hình trụ

– Công thức tính:

       

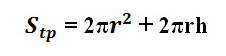
– Trong đó:

• r: bán kính hình trụ
• 2 x π x r x h : diện tích xung quanh hình trụ
• 2 x π x r^2: diện tích của hai đáy

    Ví dụ minh họa cách tính diện tích toàn phần hình trụ

Ví dụ 1: Cho một hình trụ có bán kính đường tròn đáy là 6 cm, trong khi đó chiều cao nối từ đáy tới đỉnh hình trụ dày 8 cm. Hỏi diện tích xung quanh và diện tích toàn phần của hình trụ bằng bao nhiêu ?

Theo công thức ta có bán đường tròn đáy r = 6 cm và chiều cao của hình trụ h = 8 cm. Suy ra ta có công thức tính diện tích xung quanh hình trụ và diện tích toàn phần hình trụ bằng:

– Diện tích xung quanh hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm2

– Diện tích toàn phần hình trụ = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm2.

Ví dụ 2: Tính diện tích toàn phần của hình trụ, có độ dài đường tròn đáy là 10cm, khoảng cách giữa 2 đáy là 6cm. Tính diện tích toàn phần của hình trụ đó ?

Hướng Dẫn Giải

Theo đề bài ta có: h = 6 cm; 2r = 10 cm => r = 5 cm.

Áp dụng công thức tính diện tích toàn phần hình trụ:

Vậy diện tích toàn phần của hình trụ là 110π ( cm2 )

Cám ơn bạn đã theo dõi nội dung bài viết này, hy vọng những thông tin mà chúng tôi đem đến sẽ giúp cho các bạn học sinh giải quyết được những vấn đề của mình nhé !

Người xem: 298