Định Lý Pytago đảo Là Gì ? Dùng để Làm Gì ? Lý Thuyết, Công Thức, Bài ...

Home » Toán Học » Định lý Pytago đảo là gì ? Dùng để làm gì ? Lý thuyết, công thức, bài tập có lời giải ? Toán Học Định lý Pytago đảo là gì ? Dùng để làm gì ? Lý thuyết, công thức, bài tập có lời giải ? admin.ta 15 Tháng Mười Hai, 2021 976 Views 0 SaveSavedRemoved 0

Định lý Pytago đảo là gì ? Định lý đảo sẽ có điểm gì đặc biệt sau khi bạn đã làm quen với định lý Pytago thuận. Cùng chúng tôi tìm hiểu ngay những nội dung hữu ích dưới bài viết này nhé !

Tham khảo bài viết khác:

• Trọng tâm của tam giác là gì ? Trọng tâm trong tam giác đều, cân, vuông, vuông cân
• Định lý Pitago trong tam giác vuông là gì ? Lý thuyết, bài tập Toán lớp 7, lớp 8, lớp 9

          Định lý Pytago đảo là gì ?

Tóm tắt nội dung

• 1           Định lý Pytago đảo là gì ?
• 2           Chứng minh định lý Pytago đảo ?
• 3       Định lý Pytago đảo và bài tập có lơi giải

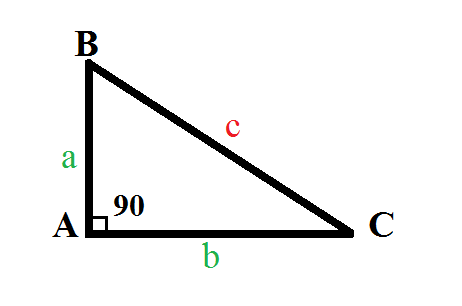
– Định lý Pytago đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

Trong ∆ABC có BC^2 = AB^2 + AC^2

=> góc BAC = 90° ==> ∆ABC vuông tại A

– Định lý Pytago đảo được sử dụng rất phổ biến cũng như gồm nhiều ứng dụng trong thực tiễn. Đây là một định lý toán học quan trọng hàng đầu của hình học cơ bản.

          Chứng minh định lý Pytago đảo ?

– Một hệ quả của định lý Pytago đảo đó là cách xác định đơn giản một tam giác có là tam giác vuông hay không, hay nó là tam giác nhọn hoặc tam giác tù.

– Gọi c là cạnh dài nhất của tam giác và có a + b > c (nếu không sẽ không tồn tại tam giác vì đây chính là bất đẳng thức tam giác). Các phát biểu sau đây là đúng:

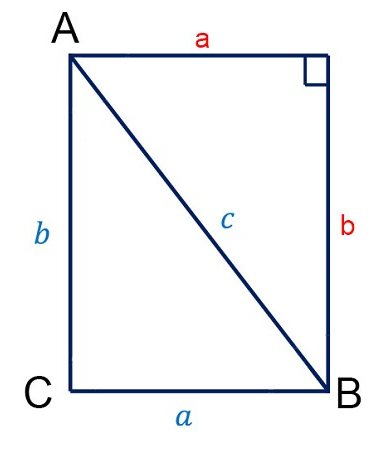
+) Nếu a^2 + b^2 = c^2 ==> thì tam giác là tam giác vuông.

Tham khảo thêm Tuổi Mão nên mua xe màu gì ? Màu xe thu hút tài lộc, may mắn

+) Nếu a^2 + b^2 > c^2 ==> thì tam giác là tam giác nhọn.

+) Nếu a^2 + b^2 < c^2 ==> thì tam giác là tam giác tù.

      Định lý Pytago đảo và bài tập có lơi giải

Bài tập 1: Cho tam giác ABC có AC= 5 cm, BC= 3 cm, AB= 4 cm. Tam giác ABC là tam giác gì ?

– Hướng dẫn giải:

Xét tam giác ABC ta có:

Ta có: AC^2 = BC^2 + AB^2 ( vì 5^2 = 3^2 + 4^2 )

==> Tam giác ABC vuông tại B ( Theo Định lí Pytago đảo)

Lưu ý: Cạnh huyền là cạnh lớn nhất trong tam giác vuông

Bài tập 2:Cho tam giác ABC có AB = 5cm AC = 12cm BC = 13 cm. Hỏi tam giác ABC có phải là tam giác vuông không ?

– Hướng dẫn giải:

Vì BC = 13 cm là cạnh lớn nhất nên đối diện với cạnh này là góc A

Ta có : BC^2 = 13^2 = 169

AB^2 + AC^2 = 5^2 + 12^2 = 169

=> BC^2 = AB^2 + AC^2

=> Tam giác ABC vuông ( theo định lí pytago đảo)

Cám ơn bạn đã theo dõi nội dung trên trang web của chúng tôi !!!

Người xem: 800