Đối Xứng Tâm Là Gì ? Hai điểm, Hai Hình đối Xứng Qua Tâm ? Lý Thuyết ...

Home » Toán Học » Đối xứng tâm là gì ? Hai điểm, hai hình đối xứng qua tâm ? Lý thuyết, ví dụ Toán Học Đối xứng tâm là gì ? Hai điểm, hai hình đối xứng qua tâm ? Lý thuyết, ví dụ admin.ta 30 Tháng Mười Hai, 2021 41 Views 0 SaveSavedRemoved 0

Đối xứng tâm là gì ? Trong bài viết dưới đây chúng tôi sẽ chia sẻ cho bạn những kiến thức cần nắm bắt và ghi nhớ trong chương trình toán 8 với những lý thuyết, tính chất, định nghĩa và ví dụ

Hãy cùng theo dõi ngay nhé !

Tham khảo bài viết khác:

• Bất phương trình bậc nhất một ẩn
• Đối xứng trục là gì ?

        Đối xứng tâm là gì ?

Tóm tắt nội dung

• 1         Đối xứng tâm là gì ?
  • 1.1     1. Hai điểm đối xứng qua một điểm
  • 1.2      2. Hai hình đối xứng qua một điểm
• 2       Hình nào có đối xứng tâm ?
  • 2.1    1. Lý thuyết
  • 2.2      2. Ví dụ minh họa

    1. Hai điểm đối xứng qua một điểm

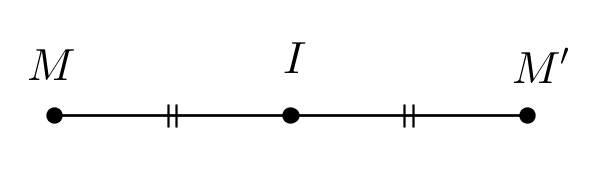
– Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm I nếu I là trung điểm của đoạn thẳng nối hai điểm đó.

==> Hai điểm M và M’ gọi là hai điểm đối xứng với nhau qua điểm I.

     2. Hai hình đối xứng qua một điểm

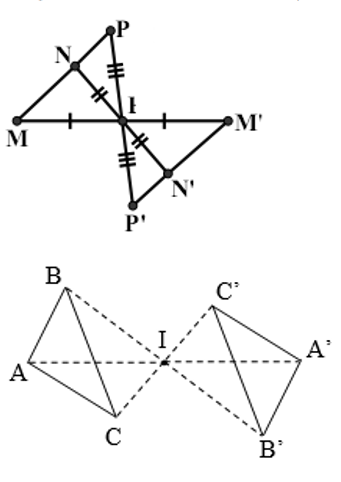
– Định nghĩa: Hai hình gọi là đối xứng với nhau qua điểm I nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm I và ngược lại.

==> Điểm I gọi là tâm đối xứng của hai hình đó.

      Hình nào có đối xứng tâm ?

   1. Lý thuyết

– Định nghĩa: Điểm I gọi là tâm đối xứng qua hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm I cũng thuộc hình H.

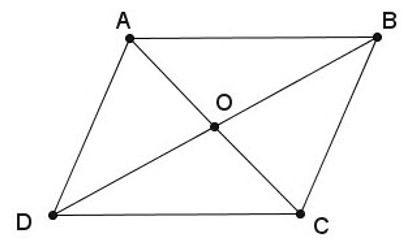
– Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.

     2. Ví dụ minh họa

Ví dụ: Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với F qua B.

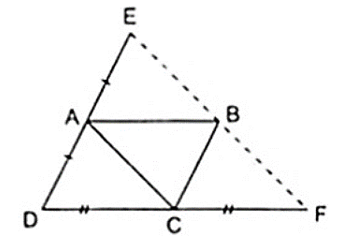
– Hướng dẫn giải:

Theo giả thiết ta có:

+ A là trung điểm của DE thì AD = AE ( 1 )

+ C là trung điểm của DF thì CD = CF ( 2 )

Ta có ABCD là hình bình hành nên AD//BC

⇒ AE//BC ( 3 ) và AD = BC ( 4 )

Từ ( 1 ), ( 4 ) ⇒ AE = BC ( 5 )

Từ ( 3 ) và ( 5 ), tứ giác ACBE có cặp cạnh đối song song và bằng nhau nên là hình bình hành.

Từ ( 6 ), ( 7 ) ⇒ E, B, F thẳng hàng và BE = BF do đó B là trung điểm của EF hay E đối xứng với F qua B.

Người xem: 515