Giải Phương Trình X+ Căn X^2- 4

Có thể bạn quan tâm

Tìm×

Tìm kiếm với hình ảnh

Vui lòng chỉ chọn một câu hỏi

Tìm đáp án

- Đăng nhập
- |
- Đăng ký

Hoidap247.com Nhanh chóng, chính xác

Hãy đăng nhập hoặc tạo tài khoản miễn phí!

Đăng nhậpĐăng ký

Đặt câu hỏi

logo

Lưu vào

+
Danh mục mới

Lưu

lenhuquynh76
Chưa có nhóm

Trả lời
2
Điểm
40
Cảm ơn
2

Toán Học
Lớp 9
10 điểm
lenhuquynh76 - 13:13:02 31/12/2019

Giải phương trình x+ căn x^2- 4 - căn x- căn x^2-4 = 3 Giúp mình với ạ trước 3h mình phải nộp rồi🙆

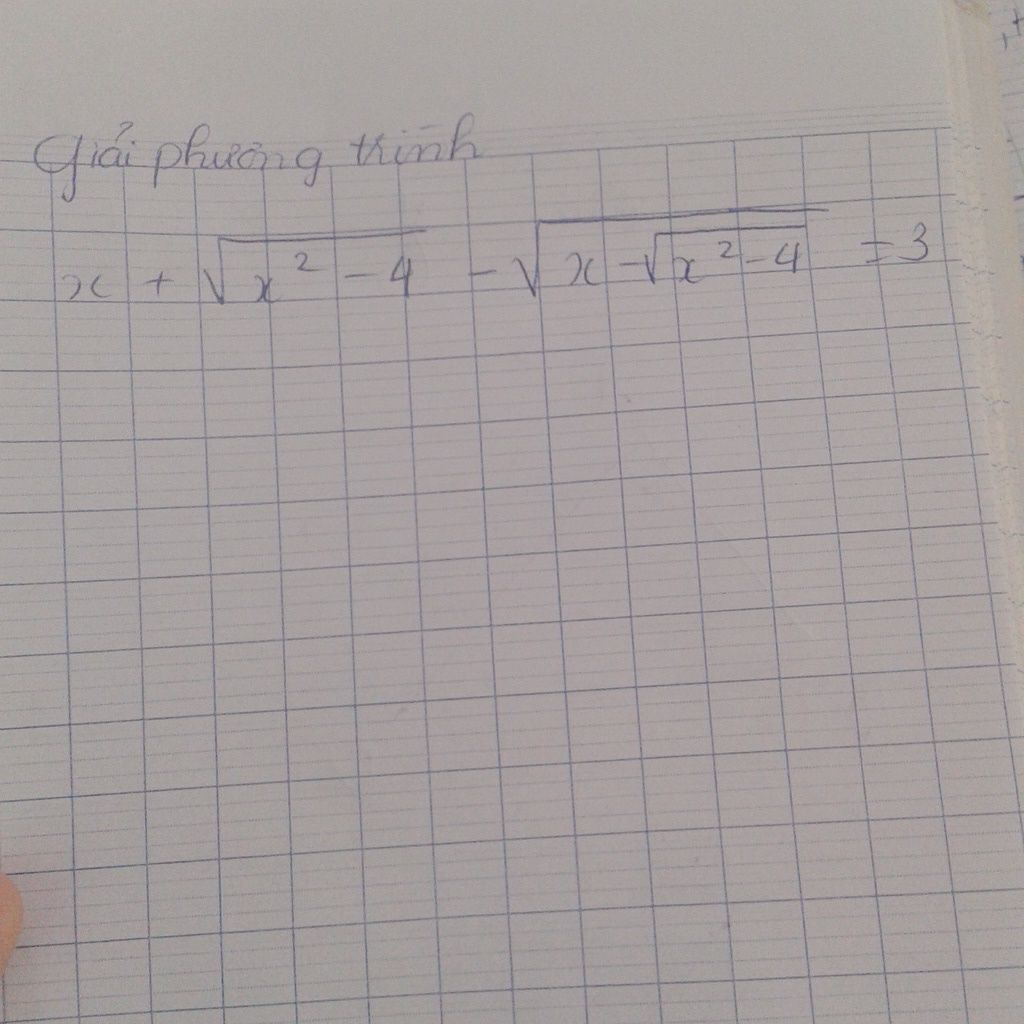
Hỏi chi tiết
Báo vi phạm

Hãy luôn nhớ cảm ơn và vote 5* nếu câu trả lời hữu ích nhé!

TRẢ LỜI

kimnguunguyen
Chưa có nhóm

Trả lời
4920
Điểm
77615
Cảm ơn
6107

kimnguunguyen

31/12/2019

Đáp án: x = 5/2

Giải thích các bước giải: Điều kiện x² - 4 ≥ 0; x - √(x² - 4) ≥ 0 ⇔ x ≥ 2

Đặt y = √[x - √(x² - 4)] > 0 ⇔ y² = x - √(x² - 4) = [x - √(x² - 4)].[x + √(x² - 4)]/[x + √(x² - 4)] = 4/[x + √(x² - 4)] ⇔ x + √(x² - 4) = 4/y²

Thay vào PT ta có:

4/y² - y = 3

⇔ y³ + 3y² - 4 = 0

⇔ (y - 1)(y + 2)² = 0

⇔ y = 1

⇔ x - √(x² - 4) = 1

⇔ x - 1 = √(x² - 4)

⇔ x² - 2x + 1 = x² - 4

⇔ x = 5/2

Hãy giúp mọi người biết câu trả lời này thế nào?

starstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstar5starstarstarstarstar1 voteGửiHủy

Cảm ơn 2
Báo vi phạm

Đăng nhập để hỏi chi tiết

Xem thêm:

>> Tuyển tập 100+ đề bài đọc hiểu Ngữ Văn lớp 9

Lethinguyet2468
Chưa có nhóm

Trả lời
1490
Điểm
10646
Cảm ơn
1009

Lethinguyet2468

Đây là một chuyên gia không còn hoạt động

31/12/2019

Giải thích các bước giải:

ĐKXĐ: x≥2 hoặc x≤-2

vì (-x)² khác (-x)²-4 với mọi x tm ĐKXĐ

=> -x khác √(x²2-4) với mọi x tm ĐKXĐ

=> x+√(x²-4) khác 0 với mọi x tm ĐKXĐ

$\begin{array}{l} x + \sqrt {x{\,^2} - 4} - \sqrt {x - \sqrt {{x^2} - 4} } = 3\\ \Leftrightarrow x + \sqrt {x{\,^2} - 4} - \frac{{\sqrt {{x^2} - ({x^2} - 4)} }}{{\sqrt {x + \sqrt {x{\,^2} - 4} } }} = 3\\ \Leftrightarrow x + \sqrt {x{\,^2} - 4} - \frac{2}{{\sqrt {x + \sqrt {x{\,^2} - 4} } }} = 3\\ \Leftrightarrow \frac{{{{(\sqrt {x + \sqrt {x{\,^2} - 4} } )}^3} - 2 - 3\sqrt {x + \sqrt {x{\,^2} - 4} } }}{{\sqrt {x + \sqrt {x{\,^2} - 4} } }} = 0\\ \Leftrightarrow {(\sqrt {x + \sqrt {x{\,^2} - 4} } )^3} - 2 - 3\sqrt {x + \sqrt {x{\,^2} - 4} } = 0\\ \Leftrightarrow (\sqrt {x + \sqrt {x{\,^2} - 4} } - 2){(\sqrt {x + \sqrt {x{\,^2} - 4} } + 1)^2} = 0\\ \Leftrightarrow \sqrt {x + \sqrt {x{\,^2} - 4} } - 2 = 0(do\,\sqrt {x + \sqrt {x{\,^2} - 4} } + 1 \ge 1 > 0)\\ \Leftrightarrow \sqrt {x + \sqrt {x{\,^2} - 4} } = 2\\ \Rightarrow x + \sqrt {{x^2} - 4} = 4\\ \Leftrightarrow \sqrt {{x^2} - 4} = 4 - x\\ \Leftrightarrow \left\{ \begin{array}{l} 4 - x \ge 0\\ {x^2} - 4 = {x^2} - 8x + 16 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} 4 \ge x\\ x = \frac{5}{2} \end{array} \right.\\ \Leftrightarrow x = \frac{5}{2} \end{array}$

(thoả mãn điều kiện xác định)

Hãy giúp mọi người biết câu trả lời này thế nào?

starstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstarstar5starstarstarstarstar2 voteGửiHủy