Giải SBT Toán 11 Bài 3: Một Số Phương Trình Lượng Giác Thường Gặp

• Trang chủ
• Lớp 11
• Toán

SBT Toán 11 Bài 3: Một số phương trình lượng giác thường gặp | Giải SBT Toán lớp 11

Mai Anh Ngày: 17-05-2022 Lớp 11 5.3 K 5.3 K

• Cách giải phương trình bậc nhất đối với sinx, cosx
• Công thức lượng giác cần nắm vững
• Chuyên đề Phương trình lượng giác thường gặp 2022 hay, chọn lọc
• 30 câu Trắc nghiệm Một số phương trình lượng giác cơ bản có đáp án 2023 – Toán lớp 11
• 20 câu Trắc nghiệm Một số phương trình lượng giác cơ bản có đáp án 2023 – Toán lớp 11 (Phần 2)
• 50 Bài tập Một số phương trình lượng giác thường gặp (có đáp án)- Toán 11
• Giải Toán 11 Bài 3: Một số phương trình lượng giác thường gặp

Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 11 Bài 3: Một số phương trình lượng giác thường gặp chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 3: Một số phương trình lượng giác thường gặp

Bài 1.25 trang 37 SBT Đại số và Giải tích 11: Giải các phương trình sau

a) cos⁡2x−sin⁡x−1=0

b) cos⁡xcos⁡2x=1+sin⁡xsin⁡2x

c) 4sin⁡xcos⁡xcos⁡2x=−1

d) tan⁡x=3cot⁡x.

Phương pháp giải:

a) Dùng công thức nhân đôi biến đổi cos⁡2x=1−2sin2x để đưa phương trình về dạng phương trình bậc hai đối với một hàm lượng giác.

b) Sử dụng công thức cosin của tổng cos⁡(a+b)=cos⁡acos⁡b−sin⁡asin⁡b đẻ rút gọn phương trình.

c) Sử dụng công thức nhân đôi sin⁡2x=2sin⁡xcos⁡x để rút gọn phương trình.

d) Tìm điều kiện xác định của phương trình.

Sử dụng công thức cot⁡x=1tan⁡x để rút gọn phương trình.

Lời giải:

a) Ta có: cos⁡2x−sin⁡x−1=0

⇔1−2sin2x−sin⁡x−1=0

⇔sin⁡x(2sin⁡x+1)=0

⇔[sin⁡x=0sin⁡x=−12

⇔[x=kπ,k∈Zx=−π6+k2π,k∈Zx=7π6+k2π,k∈Z.

b)

Ta có: cos⁡xcos⁡2x=1+sin⁡xsin⁡2x

⇔cos⁡xcos⁡2x−sin⁡xsin⁡2x=1

⇔cos⁡3x=1

⇔3x=k2π

⇔x=k2π3,k∈Z.

c)

Ta có: 4sin⁡xcos⁡xcos⁡2x=−1

⇔2sin⁡2xcos⁡2x=−1

⇔sin⁡4x=−1

⇔4x=−π2+k2π,k∈Z

⇔x=−π8+kπ2,k∈Z.

d)

ĐKXĐ: ⇔{cos⁡x≠0sin⁡x≠0

Ta có: tan⁡x=3cot⁡x

⇔tan⁡x=3tan⁡x

⇔tan2x=3

⇔tan⁡x=±3

⇒x=±π3+kπ,k∈Z

Các giá trị này thỏa mãn điều kiện của phương trình nên là nghiệm của phương trình đã cho.

Bài 1.26 trang 37 SBT đại số và giải tích 11: Giải các phương trình

a) 3cos2x−2sin⁡x+2=0

b) 5sin2x+3cos⁡x+3=0

c) sin6x+cos6x=4cos22x

d) −14+sin2x=cos4x.

Phương pháp giải:

a) Sử dụng công thức sin2x+cos2x=1 để rút gọn phương trình.

c) Rút gọn phương trình bằng cách:

Thêm bớt VT để có hằng đẳng thức số 3.

Sử dụng công thức sin2x+cos2x=1.

Sử dụng công thức nhân đôi.

Lời giải:

a) Ta có: 3cos2x−2sin⁡x+2=0

⇔3(1−sin2x)−2sin⁡x+2=0

⇔3sin2x+2sin⁡x−5=0

⇔(sin⁡x−1)(3sin⁡x+5)=0

⇔[sin⁡x−1=03sin⁡x+5=0

⇔[sin⁡x=1sin⁡x=−53(vô nghiệm)

⇔x=π2+k2π,k∈Z.

b)

Ta có: 5sin2x+3cos⁡x+3=0

⇔5(1−cos2x)+3cos⁡x+3=0

⇔5cos2x−3cos⁡x−8=0

⇔(cos⁡x+1)(5cos⁡x−8)=0

⇔[cos⁡x+1=05cos⁡x−8=0

⇔[cos⁡x=−1cos⁡x=85(vô nghiệm)

⇔x=(2k+1)π,k∈Z.

c)

Ta có: sin6x+cos6x=4cos22x

⇔(sin2x+cos2x)3−

3sin2xcos2x(sin2x+cos2x)

=4cos22x

⇔1−34sin22x=4cos22x

⇔1−34(1−cos22x)=4cos22x

⇔134cos22x=14

⇔13(1+cos⁡4x2)=1

⇔1+cos⁡4x=213

⇔cos⁡4x=−1113

⇔4x=±arccos⁡(−1113)+k2π,k∈Z

⇔x=±14arccos⁡(−1113)+kπ2,k∈Z.

d)

Ta có: −14+sin2x=cos4x

⇔−14+1−cos⁡2x2=(1+cos⁡2x2)2

⇔−1+2−2cos⁡2x=1+2cos⁡2x+cos22x

⇔cos22x+4cos⁡2x=0

⇔[cos⁡2x=0cos⁡2x=−4(vô nghiệm)

⇔2x=π2+kπ,k∈Z

⇔x=π4+kπ2,k∈Z.

Bài 1.27 trang 37 SBT đại số và giải tích 11: Giải các phương trình sau

a) 2tan⁡x−3cot⁡x−2=0

b) cos2x=3sin⁡2x+3

c) cot⁡x−cot⁡2x=tan⁡x+1

Phương pháp giải:

a) Tìm ĐKXĐ của phương trình.

Sử dụng công thức cot⁡x=1tan⁡x để rút gọn phương trình.

b)

Sử dụng công thức nhân đôi để biến đổi phương trình.

Ta thấy không là nghiệm của phương trình nên ta chia hai vế của phương trình cho để rút gọn phương trình.

Sử dụng công thức .

c)

Tìm ĐKXĐ của phương trình.

Sử dụng công thức tan⁡x=sin⁡xcos⁡x, cot⁡x=cos⁡xsin⁡x và công thức nhân đôi để rút gọn

Lời giải:

a) ĐKXĐ: {cos⁡x≠0sin⁡x≠0

Ta có: 2tan⁡x−3cot⁡x−2=0

⇔2tan⁡x−3tan⁡x−2=0

⇒2tan2x−3−2tan⁡x=0

⇔tan⁡x=1±72

⇔[x=arctan⁡(1+72)+kπ,k∈Zx=arctan⁡(1−72)+kπ,k∈Z

Các giá trị này thỏa mãn ĐKXĐ nên là nghiệm của phương trình.

b)

Ta có: cos2x=3sin⁡2x+3

⇔cos2x=6sin⁡xcos⁡x+3

Ta thấy cos⁡x=0 không là nghiệm của phương trình.

Với cos⁡x≠0 ta chia hai vế của phương trình cho cos2x ta được

1=6tan⁡x+3cos2x

⇔1=6tan⁡x+3(1+tan2x)

⇔3tan2x+6tan⁡x+2=0

⇔tan⁡x=−3±33⇔

[x=arctan⁡(−3+33)+kπ,k∈Zx=arctan⁡(−3−33)+kπ,k∈Z

Các giá trị này thỏa mãn ĐKXĐ nên là nghiệm của phương trình.

c)

ĐKXĐ:

{sin⁡x≠0sin⁡2x≠0cos⁡x≠0 ⇔sin⁡2x≠0 ⇔2x≠kπ ⇔x≠kπ2

Ta có: cot⁡x−cot⁡2x=tan⁡x+1

⇔cos⁡xsin⁡x−cos⁡2xsin⁡2x=sin⁡xcos⁡x+1

⇔cos⁡xsin⁡x−cos⁡2x2sin⁡xcos⁡x=sin⁡xcos⁡x+1

⇒2cos2x−cos⁡2x=2sin2x+sin⁡2x

⇔2(cos2x−sin2x)−cos⁡2x=sin⁡2x

⇔2cos⁡2x−cos⁡2x=sin⁡2x

⇔cos⁡2x=sin⁡2x

⇔tan⁡2x=1⇔2x=π4+kπ⇔x=π8+kπ2,k∈Z

Các giá trị này thỏa mãn ĐKXĐ nên là nghiệm của phương trình.

Bài 1.28 trang 38 SBT đại số và giải tích 11: Giải các phương trình sau

a) cos2x+2sin⁡xcos⁡x+5sin2x=2

b) 3cos2x−2sin⁡2x+sin2x=1

c) 4cos2x−3sin⁡xcos⁡x+3sin2x=1

Phương pháp giải:

a) Phương pháp giải phương trình đẳng cấp đối với sin và cos: asin2x+bsin⁡xcos⁡x+ccos2x=d

Bước 1: Xét cos⁡x=0 có là nghiệm của phương trình hay không?

Bước 2: Khi cos⁡x≠0

- Chia cả 2 vế của phương trình cho cos2x ta được: asin2xcos2x+bsin⁡xcos⁡x+c=dcos2x

- Sử dụng công thức tan⁡x=sin⁡xcos⁡x; 1cos2x=tan2x+1 đưa phương trình về dạng:

atan2x+btan⁡x+c=d(1+tan2x)⇔(a−d)tan2x+btan⁡x+c−d=0

- Giải phương trình lượng giác cơ bản của tan:

tan⁡x=tan⁡α

⇔x=α+kπ,∈Z và đối chiếu với điều kiện.

b)

Phương pháp giải phương trình đẳng cấp đối với sin và cos: asin2x+bsin⁡xcos⁡x+ccos2x=d

Bước 1: Xét cos⁡x=0 có là nghiệm của phương trình hay không?

Bước 2: Khi cos⁡x≠0

- Chia cả 2 vế của phương trình cho cos2x ta được: asin2xcos2x+bsin⁡xcos⁡x+c=dcos2x

- Sử dụng công thức tan⁡x=sin⁡xcos⁡x; 1cos2x=tan2x+1 đưa phương trình về dạng:

atan2x+btan⁡x+c=d(1+tan2x)⇔(a−d)tan2x+btan⁡x+c−d=0

- Giải phương trình lượng giác cơ bản của tan:

tan⁡x=tan⁡α

⇔x=α+kπ,∈Z và đối chiếu với điều kiện.

c)

Phương pháp giải phương trình đẳng cấp đối với sin và cos: asin2x+bsin⁡xcos⁡x+ccos2x=d

Bước 1: Xét cos⁡x=0 có là nghiệm của phương trình hay không?

Bước 2: Khi cos⁡x≠0

- Chia cả 2 vế của phương trình cho cos2x ta được: asin2xcos2x+bsin⁡xcos⁡x+c=dcos2x

- Sử dụng công thức tan⁡x=sin⁡xcos⁡x; 1cos2x=tan2x+1 đưa phương trình về dạng:

atan2x+btan⁡x+c=d(1+tan2x)⇔(a−d)tan2x+btan⁡x+c−d=0

- Giải phương trình lượng giác cơ bản của tan:

tan⁡x=tan⁡α

⇔x=α+kπ,∈Z và đối chiếu với điều kiện.

Lời giải:

a) Ta có cos2x+2sin⁡xcos⁡x+5sin2x=2

Thấy rằng cos⁡x=0 không thỏa mãn phương trình. Với cos⁡x≠0, chia hai vế của phương trình cho cos2x ta được

1+2sin⁡xcos⁡x+5sin2xcos2x=2cos2x

⇔1+2tan⁡x+5tan2x=2(1+tan2x)

⇔3tan2x+2tan⁡x−1=0

⇔[tan⁡x=−1tan⁡x=13

⇔[x=−π4+kπ,k∈Zx=arctan⁡13+kπ,k∈Z

b)

Ta có 3cos2x−2sin⁡2x+sin2x=1

Với cos⁡x=0 ta thấy VT=VP=1. Vậy phương trình có nghiệm x=π2+kπ,k∈Z

TH cos⁡x≠0, chia hai vế của phương trình cho cos2x ta được

3−4sin⁡xcos⁡x+sin2xcos2x=1cos2x

⇔3−4tan⁡x+tan2x=1+tan2x

⇔4tan⁡x=2

⇔tan⁡x=12

⇔x=arctan⁡12+kπ,k∈Z

Vậy nghiệm của phương trình là x=π2+kπ,k∈Z và x=arctan⁡12+kπ,k∈Z.

c)

Ta có 4cos2x−3sin⁡xcos⁡x+3sin2x=1

Thấy rằng cos⁡x=0 không thỏa mãn phương trình. Với cos⁡x≠0, chia hai vế của phương trình cho cos2x ta được

4−3sin⁡xcos⁡x+3sin2xcos2x=1cos2x

⇔4−3tan⁡x+3tan2x=1+tan2x

⇔2tan2x−3tan⁡x+3=0(Vô nghiệm)

Vậy phương trình vô nghiệm.

Bài 1.29 trang 38 SBT đại số và giải tích 11: Giải các phương trình sau

a) 2cos⁡x−sin⁡x=2

b) sin⁡5x+cos⁡5x=−1

c) 8cos4x−4cos⁡2x+sin⁡4x−4=0

d) sin6x+cos6+12sin⁡4x=0

Phương pháp giải:

a) -Phương trình dạng asin⁡x+bcos⁡x=c

Biến đổi VT phương trình về dạng

asin⁡x+bcos⁡x=a2+b2sin⁡(x+α)

trong đó cos⁡α=aa2+b2, sin⁡α=ba2+b2 từ đó phương trình trở thành phương trình bậc nhất đối với một hàm số lượng giác.

-Nghĩa là ta chia hai vế phương trình cho a2+b2

-Sử dụng công thức cos⁡(a−b)=cos⁡acos⁡b+sin⁡asin⁡b để thu gọn phương trình.

b)

-Phương trình dạng asin⁡x+bcos⁡x=c

Biến đổi VT phương trình về dạng

asin⁡x+bcos⁡x=a2+b2sin⁡(x+α)

trong đó cos⁡α=aa2+b2, sin⁡α=ba2+b2 từ đó phương trình trở thành phương trình bậc nhất đối với một hàm số lượng giác.

-Nghĩa là ta chia hai vế phương trình cho a2+b2

-Sử dụng công thức sin⁡(a+b)=sin⁡acos⁡b+cos⁡asin⁡b để thu gọn phương trình.

c)

-Sử dụng công thức nhân đôi để thu gọn phương trình.

-Phương trình dạng asin⁡x+bcos⁡x=c

Biến đổi VT phương trình về dạng

asin⁡x+bcos⁡x=a2+b2sin⁡(x+α)

trong đó cos⁡α=aa2+b2, sin⁡α=ba2+b2 từ đó phương trình trở thành phương trình bậc nhất đối với một hàm số lượng giác.

-Nghĩa là ta chia hai vế phương trình cho a2+b2

-Sử dụng công thức khai triển sin của một tổng để thu gọn phương trình.

Lời giải:

a) Ta có 2cos⁡x−sin⁡x=2

⇔25cos⁡x−15sin⁡x=25

Ký hiệu α là góc mà cos⁡α=25 và sin⁡α=−15

Ta thu được phương trình

cos⁡αcos⁡x+sin⁡αsin⁡x=cos⁡α

⇔cos⁡(x−α)=cos⁡α

⇔x−α=±α+k2π,k∈Z

⇔[x=2α+k2π,k∈Zx=k2π,k∈Z

Vậy phương trình có nghiệm là x=2α+k2π,k∈Z và x=k2π,k∈Z.

b)

Ta có sin⁡5x+cos⁡5x=−1

⇔12cos⁡5x+12sin⁡5x=−12

Trong đó cos⁡π4=12, sin⁡π4=12 và sin⁡(−π4)=−12

Ta thu được phương trình

cos⁡π4sin⁡5x+sin⁡π4cos⁡5x=sin⁡(−π4)

⇔sin⁡(5x+π4)=sin⁡(−π4)⇔

[5x+π4=−π4+k2π,k∈Z5x+π4=π−(−π4)+k2π,k∈Z

⇔[x=−π10+k2π5,k∈Zx=π5+k2π5,k∈Z

Vậy phương trình có nghiệm là x=−π10+k2π5,k∈Z và x=π5+k2π5,k∈Z.

c)

Ta có 8cos4x−4cos⁡2x+sin⁡4x−4=0

⇔8(1+cos⁡2x2)2

−4cos⁡2x+sin⁡4x−4=0

⇔2(1+2cos⁡2x+cos22x)

−4cos⁡2x+sin⁡4x−4=0

⇔2cos22x+sin⁡4x−2=0

⇔1+cos⁡4x+sin⁡4x−2=0

⇔cos⁡4x+sin⁡4x=1

⇔12cos⁡4x+12sin⁡4x=sin⁡π4

⇔sin⁡π4cos⁡4x+cos⁡π4sin⁡4x=sin⁡π4

⇔sin⁡(4x+π4)=sin⁡π4

⇔[4x+π4=π4+k2π,k∈Z4x+π4=π−π4+k2π,k∈Z

⇔[x=kπ2,k∈Zx=π8+kπ2,k∈Z

Vậy phương trình có nghiệm là x=kπ2,k∈Z và x=π8+kπ2,k∈Z.

d)

Ta có sin6x+cos6x+12sin⁡4x=0

⇔(sin2x+cos2x)3

−3sin2xcos2x(sin2x+cos2x)

+12sin⁡4x=0

⇔1−3sin2xcos2x+12sin⁡4x=0

⇔1−3(sin⁡2x2)2+12sin⁡4x=0

⇔1−34sin22x+12sin⁡4x=0

⇔1−341−cos⁡4x2+12sin⁡4x=0

⇔8−3+3cos⁡4x+4sin⁡4x=0

⇔3cos⁡4x+4sin⁡4x=−5

⇔35cos⁡4x+45sin⁡4x=−1

Đặt 35=sin⁡α, 45=cos⁡α ta được

sin⁡αcos⁡4x+cos⁡αsin⁡4x=−1

⇔sin⁡(4x+α)=−1

⇔4x+α=3π2+k2π,k∈Z

⇔x=3π8−α4+kπ2,k∈Z

Vậu phương trình có nghiệm là x=3π8−α4+kπ2,k∈Z.

Bài 1.30 trang 38 SBT đại số và giải tích 11: Giải các phương trình sau

a) 1+sin⁡x−cos⁡x−sin⁡2x+2cos⁡2x=0

b) sin⁡x−1sin⁡x=sin2x−1sin2x

c) cos⁡xtan⁡3x=sin⁡5x

d) 2tan2x+3tan⁡x+

2cot2x+3cot⁡x+2=0

Phương pháp giải:

a) Ta rút gọn phương trình bằng cách:

-Sử dụng công thức (sin⁡x−cos⁡x)2

=sin2x−2sin⁡xcos⁡x+cos2x

=1−sin⁡2x

-Sử dụng công thức nhân đôi cos⁡2x=cos2x−sin2x

b)

Tìm ĐKXĐ của phương trình.

Nhóm các số hạng với nhau để có nhân tử chung.

c)

Tìm ĐKXĐ

Sử dụng công thức tan⁡3x=sin⁡3xcos⁡3x

Sử dụng công thức biến đổi tích thành tổng.

d)

Tìm ĐKXĐ

Nhóm các số hạng một cách thích hợp để giải phương trình

Thêm bớt VT để có hằng đẳng thức

Lời giải:

a) Ta có:

(sin⁡x−cos⁡x)2

=sin2x−2sin⁡xcos⁡x+cos2x

=1−sin⁡2x

Do đó 1−sin⁡2x=(sin⁡x−cos⁡x)2

Khi đó: 1+sin⁡x−cos⁡x−

sin⁡2x+2cos⁡2x=0

⇔(1−sin⁡2x)+(sin⁡x−cos⁡x)+2cos⁡2x=0

⇔(sin⁡x−cos⁡x)2+(sin⁡x−cos⁡x)

+2(cos2x−sin2x)=0

⇔(sin⁡x−cos⁡x)[sin⁡x−cos⁡x+1 −2(cos⁡x+sin⁡x)]=0

⇔(sin⁡x−cos⁡x)(1−sin⁡x−3cos⁡x)=0

⇔[sin⁡x−cos⁡x=01−sin⁡x−3cos⁡x=0

⇔[sin⁡x=cos⁡xsin⁡x+3cos⁡x=1

⇔[tan⁡x=1(1)110sin⁡x+310cos⁡x=110(2)

(1)⇔x=π4+kπ,k∈Z

Giải phương trình (2) ta đặt 110=sin⁡α và 310=cos⁡α ta được cos⁡αcos⁡x+sin⁡αsin⁡x=110

⇔cos⁡(x−α)=110

⇔x−α=±arccos⁡110,k∈Z

⇔x=α±arccos⁡110,k∈Z

Vậy phương trình có nghiệm là: x=π4+kπ,k∈Z và x=α±arccos⁡110,k∈Z

b)

ĐKXĐ: sin⁡x≠0

Ta có: sin⁡x−1sin⁡x=sin2x−1sin2x

⇔(sin⁡x−sin2x)+

(1sin2x−1sin⁡x)=0

⇔sin⁡x(1−sin⁡x)+1−sin⁡xsin2x=0

⇔(1−sin⁡x)(sin3x+1)=0

⇔[sin⁡x=1sin⁡x=−1

⇔[x=π2+k2π,k∈Z(thỏa mãn)x=−π2+k2π,k∈Z(thỏa mãn)

⇔x=π2+kπ,k∈Z.

c)

ĐKXĐ: cos⁡3x≠0

⇔x≠π6+kπ3,k∈Z

Ta có: cos⁡xtan⁡3x=sin⁡5x

⇔cos⁡xsin⁡3xcos⁡3x=sin⁡5x

⇔cos⁡xsin⁡3x=sin⁡5xcos⁡3x

⇔12(sin⁡4x+sin⁡2x)

=12(sin⁡8x+sin⁡2x)

⇔sin⁡8x=sin⁡4x

⇔[8x=4x+k2π,k∈Z8x=π−4x+k2π,k∈Z

⇔[x=kπ2,k∈Zx=π12+kπ6,k∈Z

Kết hợp với ĐKXĐ ta được nghiệm của phương trình là x=kπ,k∈Z và x=π12+kπ6,k∈Z.

d)

ĐKXĐ: cos≠0 và sin⁡x≠0.

Ta có: 2tan2x+3tan⁡x+

2cot2x+3cot⁡x+2=0

⇔(2tan2x+2cot2x)

+(3tan⁡x+3cot⁡x)+2=0

⇔2[(tan⁡x+cot⁡x)2−2tan⁡xcot⁡x]+

3(tan⁡x+cot⁡x)+2=0

⇔2[(tan⁡x+cot⁡x)2−2]+

3(tan⁡x+cot⁡x)+2=0

Đặt tan⁡x+cot⁡x=t ta được phương trình 2t2+3t−2=0

⇔[t=−2t=12

Với t=−2 ta có tan⁡x+cot⁡x=−2

⇒tan⁡x+1tan⁡x=−2

⇒tan2x+1=−2tan⁡x

⇒tan⁡x=−1

⇒x=−π4+kπ,k∈Z(thỏa mãn)

Với t=12 ta có tan⁡x+cot⁡x=12

⇒tan⁡x+1tan⁡x=12

⇒2tan2x+2=tan⁡x(Vô nghiệm)

Vậy phương trình có nghiệm là x=−π4+kπ,k∈Z

Bài 1.31 trang 38 SBT đại số và giải tích 11: Giải phương trình cot⁡x−tan⁡x+4sin⁡2x=2sin⁡2x Phương pháp giải:

Tìm ĐKXĐ của phương trình.

Sử dụng công thức tan⁡x=sin⁡xcos⁡x và cot⁡x=cos⁡xsin⁡x để biến đổi phương trình.

Sử dụng công thức nhân đôi.

Sử dụng công thức sin2x+cos2x=1.

Lời giải:

ĐKXĐ: sin⁡x≠0 và cos⁡x≠0 ⇔sin⁡2x≠0

⇔cos⁡2x≠±1

Ta có: cot⁡x−tan⁡x+4sin⁡2x=2sin⁡2x

⇔cos⁡xsin⁡x−sin⁡xcos⁡x+4sin⁡2x=2sin⁡2x

⇔cos2x−sin2xsin⁡xcos⁡x+4sin⁡2x=2sin⁡2x

⇔cos⁡2xsin⁡2x2+4sin⁡2x=2sin⁡2x

⇔2cos⁡2xsin⁡2x+4sin⁡2x=2sin⁡2x

⇔2cos⁡2x+4sin22x=2

⇔2cos⁡2x+4(1−cos22x)=2

⇔4cos22x−2cos⁡2x+2=0

⇔[cos⁡2x=1(loại)cos⁡2x=−12

⇔2x=±2π3+k2π,k∈Z

⇔x=±π3+kπ,k∈Z.

Cách khác:

Đặt t = tanx

Điều kiện t ≠ 0

Phương trình đã cho có dạng

Bài 1.32 trang 38 SBT đại số và giải tích 11: Nghiệm của phương trình 3cot⁡x−3=0 là

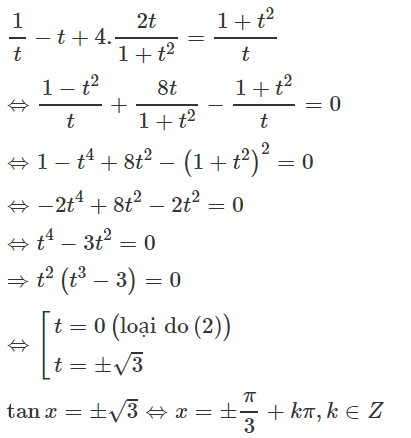
A. π6+kπ(k∈Z)

B. π3+kπ(k∈Z)

C. π4+kπ(k∈Z)

D. π6+k2π(k∈Z).

Phương pháp giải:

Phương trình: cot⁡x=cot⁡α có nghiệm là x=α+kπ,k∈Z

Sử dụng: cot⁡α=a khi đó tan⁡α=1a

Khi đó α=arctan⁡1a=arccota

Lời giải:

Ta có: 3cot⁡x−3=0

⇔cot⁡x=33

⇔cot⁡x=cot⁡π3

⇔x=π3+kπ,k∈Z

Đáp án: B.

Bài 1.33 trang 38 SBT đại số và giải tích 11: Nghiệm của phương trình sau sin4x−cos4x=0 là

A. π2+kπ(k∈Z)

B. π3+kπ(k∈Z)

C. π4+kπ2(k∈Z)

D. π6+kπ(k∈Z).

Phương pháp giải:

Khai triển phương trình theo hằng đẳng thức số 2.

Sử dụng công thức nhân đôi cos⁡2x=cos2x−sin2x.

Phương trình cos⁡x=a

Nếu |a|>1 phương trình vô nghiệm

Nếu |a|≤1 khi đó phương trình có nghiệm là

x=±arccos⁡a+k2π,k∈Z.

Lời giải:

Ta có: sin4x−cos4x=0

⇔(sin2x−cos2x)(sin2x+cos2x)=0

⇔−cos⁡2x=0

⇔cos⁡2x=0

⇔2x=π2+kπ,k∈Z

⇔x=π4+kπ2,k∈Z

Đáp án: C.

Bài 1.34 trang 38 SBT đại số và giải tích 11: Cho phương trình 4cos22x+16sin⁡xcos⁡x−7=0(1)

Xét các giá trị (I)π6+kπ

(II)5π12+kπ(k∈Z).

(III)π12+kπ

Trong các giá trị trên giá trị nào là nghiệm của phương trình (1) ?

A. Chỉ (I)

B. Chỉ (II)

C. Chỉ (III)

D. (II) và (III)

Phương pháp giải:

Sử dụng công thức nhân đôi sin⁡2x=2sin⁡xcos⁡x.

Sử dụng công thức sin2x+cos2x=1 để đưa phương trình dạng phương trình bậc hai đối với hàm số sin⁡2x.

Phương trình sin⁡x=a

Nếu |a|>1 phương trình vô nghiệm

Nếu |a|≤1 khi đó phương trình có nghiệm là

x=arcsin⁡a+k2π,k∈Z

và x=π−arcsin⁡a+k2π,k∈Z.

Lời giải:

Ta có: (1)⇔4(1−sin22x)+8sin⁡2x−7=0

⇔4sin22x−8sin⁡2x+3=0

⇔[sin⁡2x=32>1(loại)sin⁡2x=12

⇔[2x=π6+k2π,k∈Z2x=π−(π6)+k2π,k∈Z

⇔[x=π12+kπ,k∈Zx=5π12+kπ,k∈Z

Vậy phương trình có nghiệm là x=π12+kπ,k∈Z và x=5π12+kπ,k∈Z.

Đáp án: D.

Bài 1.35 trang 39 SBT đại số và giải tích 11: Nghiệm của phương trình cos⁡xcos⁡7x=cos⁡3xcos⁡5x là

A. π6+kπ,k∈Z

B. −π6+k2π,k∈Z

C. kπ4,k∈Z

D. kπ3,k∈Z.

Phương pháp giải:

Sử dụng công thức biến đổi tích thành tổng.

Phương trình cos⁡x=cos⁡α có nghiệm là

x=±α+k2π,k∈Z.

Lời giải:

Ta có: cos⁡xcos⁡7x=cos⁡3xcos⁡5x

⇔12[cos⁡(7x+x)+cos⁡(7x−x)]

=12[cos⁡(5x+3x)+cos⁡(5x−3x)]

⇔cos⁡8x+cos⁡6x=cos⁡8x+cos⁡2x

⇔cos⁡6x=cos⁡2x

⇔[6x=2x+k2π,k∈Z6x=−2x+k2π,k∈Z

⇔[x=kπ2,k∈Zx=kπ4,k∈Z

Vì tập {kπ2}⊂{kπ4}

Vậy nghiệm của phương trình là kπ4,k∈Z

Đáp án: C

Bài 1.36 trang 39 SBT đại số và giải tích 11: Nghiệm của phương trình 3tan⁡2x+6cot⁡x=−tan⁡x là

A. kπ4,k∈Z

B. ±π3+kπ,k∈Z

C. π6+kπ,k∈Z

D. kπ2,k∈Z.

Phương pháp giải:

Tìm ĐKXĐ.

-Sử dụng công thức khai triển tan của một tổng tan⁡(a+b)=tan⁡a+tan⁡b1−tan⁡atan⁡b trong bài là a=b=x nên ta có tan⁡2x=2tan⁡x1−tan2x.

-Sử dụng cot⁡x=1tan⁡x

-Phương trình: tan⁡x=a có α thỏa mãn tan⁡α=a

hay viết là α=arctan⁡a

Khi đó phương trình có nghiệm là x=α+kπ,k∈Z.

Lời giải:

ĐKXĐ: cos⁡2x≠0, sin⁡x≠0 và cos⁡x≠0

⇔cos⁡2x≠0 và sin⁡2x≠0

⇔sin⁡4x≠0

⇔4x≠kπ,k∈Z

⇔x≠kπ4,k∈Z

Ta có: 3tan⁡2x+6cot⁡x=−tan⁡x

⇔32tan⁡x1−tan2x+6tan⁡x+tan⁡x=0

⇔6tan2x+6−6tan2x+tan2x(1−tan2x)=0

⇔−tan4x+tan2x+6=0

⇔[tan2x=−2<0(loại)tan2x=3

⇔tan⁡x=±3

⇔x=±π3+kπ,k∈Z

Đáp án: B.

Cách trắc nghiệm:

Điều kiện của phương trình:

x ≠ kπ, x ≠ π/2 + kπ, x ≠ π/4 + kπ/2 (k ∈ Z)

Xét các phương án.

- Vì π/4 và π/2 không thỏa mãn điều kiện của phương trình nên hai phương án A và D bị loại.

- Với x = π/6 thì vế phải của phương trình đã cho âm, còn vế trái dương, nên phương án C bị loại.

Bài 1.37 trang 39 SBT đại số và giải tích 11: Nghiệm của phương trình 2sin⁡x=3cot⁡x là

A. π6+k2π,k∈Z

B. kπ2,k∈Z

C. π4+k2π,k∈Z

D. ±π3+k2π,k∈Z

Phương pháp giải:

Tìm ĐKXĐ.

- Sử dụng công thức cot⁡x=cos⁡xsin⁡x.

- Sử dụng công thức sin2x+cos2x=1.

Lời giải:

ĐKXĐ: sin⁡x≠0

⇔x≠kπ,k∈Z

Ta có: 2sin⁡x=3cot⁡x

⇔2sin⁡x=3cos⁡xsin⁡x

⇔2sin2x=3cos⁡x

⇔2(1−cos2x)−3cos⁡x=0

⇔2cos2x+3cos⁡x−2=0

⇔[cos⁡x=−2<−1(loại)cos⁡x=12

⇔x=±π3+k2π,k∈Z(thỏa mãn)

Đáp án: D.

Cách trắc nghiệm:

Xét các phương án.

- Với x = π/6 thì vế trái của phương trình bằng 1, còn vế phải là 3√3 nên phương án A bị loại.

- Giá trị kπ/2 với k = 2 không thỏa mãn điều kiện của phương trình nên phương án B bị loại.

- Với x = π/4 thì vế trái của phương trình bằng √2, còn vế phải bằng 3, nên phương án C bị loại.

Bài 1.38 trang 39 SBT đại số và giải tích 11: Cho phương trình 3cos⁡x+sin⁡x=2(*)

Xét các giá trị

(I)π2+k2π(II)π3+k2π(III)π6+k2π(k∈Z).

Trong các giá trị trên, giá trị nào à nghiệm của phương trình (*)?

A. Chỉ (I)

B. Chỉ (II)

C. Chỉ (III)

D. (I) và (III)

Phương pháp giải:

Cách giải phương trình dạng asin⁡x+bcos⁡x=c

Ta chia hai vế phương trình cho a2+b2

Đặt sin⁡α=aa2+b2 và cos⁡α=ba2+b2

Sau đó sử dụng công thức khai triển cos của một hiệu cos⁡(a−b)=cos⁡acos⁡b+sin⁡asin⁡b để đưa phương trình về dạng cos⁡x=a.

Lời giải:

Ta có: (*)⇔32cos⁡x+12sin⁡x=1

⇔cos⁡(x−π6)=1

⇔x−π6=k2π,k∈Z

⇔x=π6+k2π,k∈Z

Đáp án: C.

Từ khóa :

Giải sách bài tập Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức Tam giác đều: Định nghĩa, tính chất, dấu hiệu nhận biết tam giác đều Admin Vietjack 1 K Toán Tổng hợp kiến thức Dấu hiệu nhận biết hình vuông 2025 và bài tập vận dụng Admin Vietjack 633 Toán Tổng hợp kiến thức Công thức tính tổng dãy số cách đều 2025 chính xác nhất Admin Vietjack 873 Toán Tổng hợp kiến thức Dấu hiệu nhận biết hình bình hành 2025 hay, chi tiết nhất Admin Vietjack 667

Tìm kiếm

Tìm kiếm

Bài Viết Xem Nhiều

• 1. Giải sgk Toán 11 Chân trời sáng tạo | Giải bài tập Toán 11 Tập 1, Tập 2 Chân trời sáng tạo (hay, chi tiết) 75.4 K
• 2. Giải sgk Toán 11 Kết nối tri thức | Giải bài tập Toán 11 Kết nối tri thức Tập 1, Tập 2 (hay, chi tiết) 74.6 K
• 3. Lý thuyết Toán 11 Kết nối tri thức | Tổng hợp kiến thức Toán 11 Kết nối tri thức hay, chi tiết 66.4 K
• 4. Giải sgk Toán 11 Cánh diều | Giải bài tập Toán 11 Cánh diều Tập 1, Tập 2 (hay, chi tiết) 48.6 K
• 5. Giải SBT Toán 11 Cánh diều | Sách bài tập Toán 11 Cánh diều (hay, chi tiết) 44.9 K

Đánh giá tài liệu

× Gửi đánh giá

Báo cáo tài liệu vi phạm

× Sai môn học, lớp học Tài liệu chứa link, quảng cáo tới các trang web khác Tài liệu chất lượng kém Tài liệu sai, thiếu logic, tài liệu chứa thông tin giả Nội dung spam nhiều lần Tài liệu có tính chất thô tục, cổ súy bạo lực Khác Báo cáo

Ẩn tài liệu vi phạm

× Lý do ẩn Ẩn

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.