Giải Toán 8 Bài 1: Nhân đơn Thức Với đa Thức

Giải Toán 8 bài 1 Sách mớiChân trời sáng tạo, Kết nối tri thức, Cánh diềuBài trướcBài sauNâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi. Mua ngay Từ 79.000đ Tìm hiểu thêm

Giải Toán 8 Bài 1 bộ 3 sách mới: Chân trời sáng tạo, Kết nối tri thức, Cánh diều được VnDoc tổng hợp lời giải Toán 8, giúp các em học sinh nắm vững kiến thức, luyện giải bài tập môn Toán lớp 8. Mời các em tham khảo.

Giải bài tập Toán 8 bài 1

• 1. Giải Toán 8 tập 1 Kết nối tri thức Bài 1
  • Bài tập 1.1 trang 9 sgk Toán 8 tập 1 KNTT:
  • Bài tập 1.2 trang 9 sgk Toán 8 tập 1 KNTT:
  • Bài tập 1.3 trang 10 sgk Toán 8 tập 1 KNTT:
  • Bài tập 1.4 trang 10 sgk Toán 8 tập 1 KNTT:
  • Bài tập 1.5 trang 10 sgk Toán 8 tập 1 KNTT:
  • Bài tập 1.6 trang 10 sgk Toán 8 tập 1 KNTT:
  • Bài tập 1.7 trang 10 sgk Toán 8 tập 1 KNTT:
• 2. Giải Toán 8 tập 1 Chân trời sáng tạo Bài 1
  • Bài tập 1 trang 11 sgk Toán 8 tập 1 CTST:
  • Bài tập 2 trang 11 sgk Toán 8 tập 1 CTST:
  • Bài tập 3 trang 11 sgk Toán 8 tập 1 CTST:
  • Bài tập 4 trang 11 sgk Toán 8 tập 1 CTST:
  • Bài tập 5 trang 11 sgk Toán 8 tập 1 CTST:
• 3. Giải Toán 8 tập 1 Cánh diều bài 1
  • Bài tập 1 trang 9 sgk Toán 8 tập 1 CD:
  • Bài tập 2 trang 10 sgk Toán 8 tập 1 CD:
  • Bài tập 3 trang 10 sgk Toán 8 tập 1 CD:
  • Bài tập 4 trang 10 sgk Toán 8 tập 1 CD:
  • Bài tập 5 trang 10 sgk Toán 8 tập 1 CD:
  • Bài tập 6 trang 10 sgk Toán 8 tập 1 CD:
  • Bài tập 6 trang 10 sgk Toán 8 tập 1 CD:
  • Bài tập 7 trang 10 sgk Toán 8 tập 1 CD:

1. Giải Toán 8 tập 1 Kết nối tri thức Bài 1

Bài tập 1.1 trang 9 sgk Toán 8 tập 1 KNTT:

Trong các biểu thức sau, biểu thức nào là đơn thức?

\(-x;(1+x)y^{2};(3+\sqrt{3})xy;0;\frac{1}{y}x^{2};2\sqrt{xy}\)

Hướng dẫn giải:

\(-x;(3+\sqrt{3})xy;0\)

Bài tập 1.2 trang 9 sgk Toán 8 tập 1 KNTT:

Cho các đơn thức:

\(A=4x(-2)x^{2}y;B=12,75xyz;C=(1+2\times 4,5)x^{2}y\frac{1}{5}y^{3}; D=(2-\sqrt{5})x\)

a) Liệt kê các đơn thức thu gọn trong các đơn thức đã cho và thu gọn các đơn thức còn lại.

b) Với mỗi đơn thức nhận được, hãy cho biết hệ số, phần biến và bậc của nó.

Hướng dẫn giải:

a) Các đơn thức đã thu gọn: B, D

\(A=4x(-2)x^{2}y=-8x^{3}\)

\(C=(1+2\times 4,5)x^{2}y\frac{1}{5}y^{3}=2x^{2}y^{4}\)

b) Hệ số của đơn thức A là -8, phần biến là x3y và bậc là 4

Hệ số của đơn thức B là 12,75, phần biến xyz là và bậc là 3

Hệ số của đơn thức C là 2, phần biến là x2y4 và bậc là 6

Hệ số của đơn thức A là \(2-\sqrt{5}\), phần biến là x và bậc là 1

Bài tập 1.3 trang 10 sgk Toán 8 tập 1 KNTT:

Thu gọn rồi tính giá trị của mỗi đơn thức sau:

a) \(A=(-2)x^{2}y\frac{1}{2}xy;\) khi \(x = -2; y=\frac{1}{2}\)

b) \(B=xyz(-0,5)y^{2}z\) khi x = 4; y = 0,5; z = 2.

Hướng dẫn giải:

a) \(A=(-2)x^{2}y\frac{1}{2}xy=-x^{3}y^{2}\)

Thay \(x = -2; y=\frac{1}{2}\) vào A, ta có:

\(A=-(-2)^{3}\times (\frac{1}{2})^{2}=2\)

b) \(B=xyz(-0,5)y^{2}z=-0,5xy^{3}z^{2}\)

Thay x = 4; y = 0,5; z = 2 vào B ta có:

\(B= -0,5\times 4\times 0,5^{3}\times 2^{2}=-1\)

Bài tập 1.4 trang 10 sgk Toán 8 tập 1 KNTT:

Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau:

\(3x^{3}y^{2};-0,2x^{2}y^{3};7x^{3}y^{2};-4y;\frac{3}{4}x^{2}y^{3};y\sqrt{2}\)

Hướng dẫn giải:

Nhóm 1: \(3x^{3}y^{2};7x^{3}y^{2}\)

Nhóm 2: \(-0,2x^{2}y^{3};\frac{3}{4}x^{2}y^{3}\)

Nhóm 3: \(-4y;y\sqrt{2}\)

Bài tập 1.5 trang 10 sgk Toán 8 tập 1 KNTT:

Rút gọn rồi tính giá trị của biểu thức

\(S=\frac{1}{2}x^{2}y^{5}-\frac{5}{2}x^{2}y^{5}\) khi x = -2 và y = 1

Hướng dẫn giải:

\(S=\frac{1}{2}x^{2}y^{5}-\frac{5}{2}x^{2}y^{5}=-2x^{2}y^{5}\)

Thay x = -2, y = 1 vào S ta có:

\(-2\times (-2)^{2}\times 1^{5}=-8\)

Bài tập 1.6 trang 10 sgk Toán 8 tập 1 KNTT:

Tính tổng của bốn đơn thức:

\(2x^{2}y^{3};-\frac{3}{5}x^{2}y^{3};-14x^{2}y^{3};\frac{8}{5}x^{2}y^{3}\)

Hướng dẫn giải:

\(2x^{2}y^{3}+-\frac{3}{5}x^{2}y^{3}+-14x^{2}y^{3}+\frac{8}{5}x^{2}y^{3}\)

\(=(2-\frac{3}{5}-14+\frac{8}{5})x^{2}y^{3}=-11x^{2}y^{3}\)

Bài tập 1.7 trang 10 sgk Toán 8 tập 1 KNTT:

Một mảnh đất có dạng như phần được tô màu xanh trong hình bên cùng với các kích thước được ghi trên đó. Hãy tìm đơn thức (thu gọn) với hai biến x và y biểu thị diện tích của mảnh đất đã cho bằng hai cách:

Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC

Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA

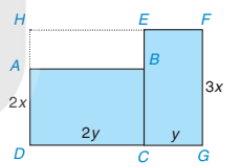
Hướng dẫn giải:

Cách 1: \(S = {S_{ABCD}} + {S_{EFGC}} = 2x.2y + y.3x = 4xy + 3xy = \left( {4 + 3} \right)xy = 7xy.\)

Cách 2:

\(\begin{array}{l}S = {S_{HFGD}} - {S_{HEBA}} = \left( {2y + y} \right).3x - \left( {3x - 2x} \right).2y\\ = 3y.3x - x.2y = 9xy - 2xy = \left( {9 - 2} \right)xy = 7xy.\end{array}\)

2. Giải Toán 8 tập 1 Chân trời sáng tạo Bài 1

Bài tập 1 trang 11 sgk Toán 8 tập 1 CTST:

Chỉ ra các đơn thức, đa thức trong các biểu thức sau:

\(-3;2z;\frac{1}{3}xy+1;-10x^{2}yz;\frac{4}{xy};5x-\frac{z}{2};1+\frac{1}{y}\)

Hướng dẫn giải

Các đơn thức: \(-3;2z;-10x^{2}yz\)

Bài tập 2 trang 11 sgk Toán 8 tập 1 CTST:

Thu gọn các đơn thức sau. Chỉ ra hệ số, phần biến và bậc của mỗi đơn thức.

\(5xyx; -xyz\frac{2}{3}y;-2x^{2}(-\frac{1}{6})x\)

Hướng dẫn giải

\(5xyx=5x^{2}y\) có hệ số là 5, phần biến là \(x^{2}y\), bậc bằng 3

\(-xyz\frac{2}{3}y=-\frac{2}{3}xy^{2}z\) có hệ số là \(-\frac{2}{3}\), phần biến là \(xy^{2}z\), bậc bằng 4

\(-2x^{2}(-\frac{1}{6})x=\frac{1}{3}x^{3}\)có hệ số là \(\frac{1}{3}\), phần biến là \(x^{3}\), bậc bằng 3

Bài tập 3 trang 11 sgk Toán 8 tập 1 CTST:

Thu gọn và tìm bậc của mỗi đa thức sau:

a) \(M = x - 3 - 4y + 2x - y\)

b) \(N=-x^{2}t+13t^{3}+xt^{2}+5t^{3}-4\)

Hướng dẫn giải

a) \(M = x - 3 - 4y + 2x - y = 3x -5y -3\) có bậc bằng 1

b) \(N=-x^{2}t+13t^{3}+xt^{2}+5t^{3}-4\)

\(=-x^{2}t+18t^{3}+xt^{2}-4\) có bậc bằng 3

Bài tập 4 trang 11 sgk Toán 8 tập 1 CTST:

Tính giá trị của đa thức \(P=3xy^{2}-6xy+8xz+xy^{2}-10xz\) tại \(x=-3;y=-\frac{1}{2};z=3\)

Hướng dẫn giải

\(P=3xy^{2}-6xy+8xz+xy^{2}-10xz\)

\(=4xy^{2}-6xy-2xz\)

Thay \(x=-3;y=-\frac{1}{2};z=3\) vào P ta có:

\(4\times (-3)\times (-\frac{1}{2})^{2}-6\times (-2)\times (-\frac{1}{2})-2\times (-3)\times 3=9\)

Bài tập 5 trang 11 sgk Toán 8 tập 1 CTST:

Viết biểu thức biểu thị thể tích V và diện tích xung quanh S của hình hộp chữ nhật trong Hình 5. Tính giá trị của V, S khi x = 4 cm, y = 2 cm và z = 1 cm

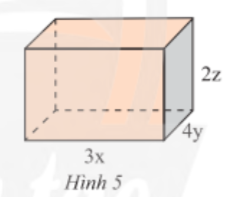
Hướng dẫn giải

\(V=2x\times 4y\times 2z=24xyz(cm^{3})\)

\(S=2\times 2z\times (3x+4y)=12xz+16yz(cm^{2})\)

Thay x = 4, y = 2, z = 1 vào V ta có: \(24\times 4\times 2\times 1=192(cm^{3})\)

Thay x = 4, y = 2, z = 1 vào S ta có: \(12\times 4\times 1+16\times 2\times 1=80(cm^{2})\)

3. Giải Toán 8 tập 1 Cánh diều bài 1

Bài tập 1 trang 9 sgk Toán 8 tập 1 CD:

a. Trong những biểu thức sau, biểu thức nào là đơn thức?

\(\frac{1}{5}xy^{2}z^{3}; 3 - 2x^{3}y^{2}z; -\frac{3}{2}x^{4}yxz^{2}; \frac{1}{2}x^{2}(y^{3}-z^{3})\)

b. Trong những biểu thức sau, biểu thức nào là đa thức?

\(2-x+y; - 5x^{2}yz^{3} + \frac{1}{3}xy^{2}z + x + 1; \frac{x-y}{xy^{2}}; \frac{1}{x} + 2y - 3z\)

Hướng dẫn giải

a. Những biểu thức là đơn thức là:

\(\frac{1}{5}xy^{2}z^{3}; 3 - 2x^{3}y^{2}z; -\frac{3}{2}x^{4}yxz^{2}\)

b. Những biểu thức là đa thức là:

\(2-x+y; - 5x^{2}yz^{3} + \frac{1}{3}xy^{2}z + x + 1; \frac{1}{x} + 2y - 3z\)

Bài tập 2 trang 10 sgk Toán 8 tập 1 CD:

Thu gọn mỗi đơn thức sau:

\(a. -\frac{1}{2}x^{2}yxy^{3}\)

\(b. 0,5x^{2}yzxy^{3}\)

Hướng dẫn giải

Thu gọn mỗi đơn thức sau:

\(a. -\frac{1}{2}x^{2}yxy^{3} = -\frac{1}{2}x^{2+1}y^{3+1} = -\frac{1}{2}x^{3}y^{4}\)

\(b. 0,5x^{2}yzxy^{3} = 0,5x^{2+1}y^{3+1}z = 0,5x^{3}y^{4}z\)

Bài tập 3 trang 10 sgk Toán 8 tập 1 CD:

Các đơn thức trong mỗi trường hợp sau có đồng dạng hay không? Vì sao?

a. \(x^{3}y^{5}; -\frac{1}{6}x^{3}y^{5}\) và \(\sqrt{3}x^{3}y^{5}\)

\(b. x^{2}y^{3} và x^{2}y^{7}\)

Hướng dẫn giải

a. Các đơn thức này là đồng dạng vì có cùng biến là \(x^{3}y^{5}\)

b. Các đơn thức này là không đồng dạng vì có khác biến.

Bài tập 4 trang 10 sgk Toán 8 tập 1 CD:

Thực hiện phép tính

\(a. 9x^{3}y^{6} + 4x^{3}y^{6} + 7x^{3}y^{6}\)

\(b. 9x^{5}y^{6} - 14x^{5}y^{6}+ 5x^{5}y^{6}\)

Hướng dẫn giải

Thực hiện phép tính

\(a. 9x^{3}y^{6} + 4x^{3}y^{6} + 7x^{3}y^{6} = (9+4+7)x^{3}y^{6} = 20x^{3}y^{6}\)

\(b. 9x^{5}y^{6} - 14x^{5}y^{6}+ 5x^{5}y^{6} = (9-14+5)x^{5}y^{6} = 0\)

Bài tập 5 trang 10 sgk Toán 8 tập 1 CD:

Thu gọn mỗi đa thức sau:

\(a. A = 13x^{2}y+ 4 + 8xy-6x^{2}y-9\)

\(b. B = 4,4x^{2}y-40,6xy^{2}+3,6xy^{2}-1,4x^{2}y-26\)

Hướng dẫn giải

Thu gọn mỗi đa thức sau:

\(a. A = 13x^{2}y+ 4 + 8xy-6x^{2}y-9 = (13-6)x^{2}y + 8xy+ (4-9)\)

\(=  7x^{2}y + 8xy-5\)

\(b. B = 4,4x^{2}y-40,6xy^{2}+3,6xy^{2}-1,4x^{2}y-26\)

\(= (4,4- 1,4)x^{2}y-(40,6-3,6)xy^{2}-26  = 3x^{2}y-37xy^{2}-26\)

Bài tập 6 trang 10 sgk Toán 8 tập 1 CD:

Tính giá trị của đa thức:

\(P = x^{3}y-14y^{3}-6xy^{2}+y+2\)tại x=-1;y=2

Hướng dẫn giải

Tại x=-1;y=2, giá trị của P là:

\(P = x^{3}y-14y^{3}-6xy^{2}+y+2\)

\(= (-1)^{3}.2-14.2^{3}-6(-1).2^{2}+2+2 = -86\)

Bài tập 6 trang 10 sgk Toán 8 tập 1 CD:

Tính giá trị của đa thức:

\(P = x^{3}y-14y^{3}-6xy^{2}+y+2\)tại x=-1;y=2

Hướng dẫn giải

Tại x=-1;y=2, giá trị của P là:

\(P = x^{3}y-14y^{3}-6xy^{2}+y+2\)

\(= (-1)^{3}.2-14.2^{3}-6(-1).2^{2}+2+2 = -86\)

Bài tập 7 trang 10 sgk Toán 8 tập 1 CD:

a. Viết đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật có ba kích thước lần lượt là x (cm), 2y (cm), 3z (cm).

b. Tính giá trị của S tại x = 6; y = 2; z = 3

Hướng dẫn giải

a. Viết đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật có ba kích thước lần lượt là x (cm), 2y (cm), 3z (cm):

Giả sử gọi kích thước chiều rộng, chiều dài và độ cao của hình hộp chữ nhật lần lượt là x,2y,3z. Khi đó:

S = 2.3z(x + 2y) + 2x.2y = 6xz + 12yz + 4xy (cm2).

b. Tại x = 6; y = 2; z = 3, S= 6.6.3 + 12.2.3 + 4.6.2 = 228 (cm2).