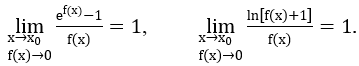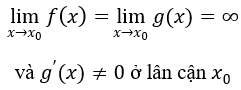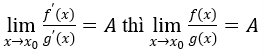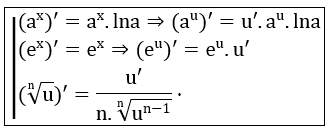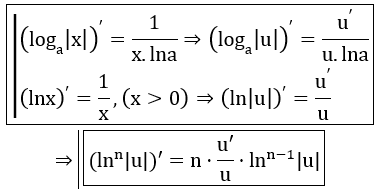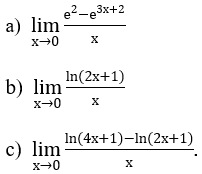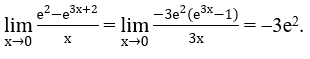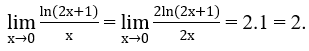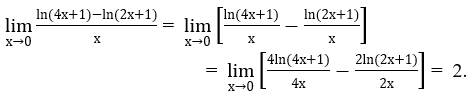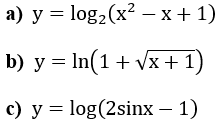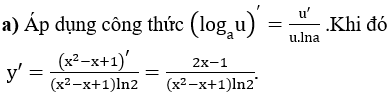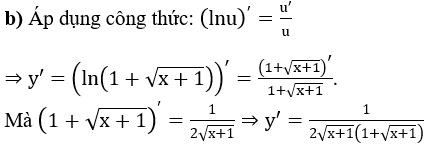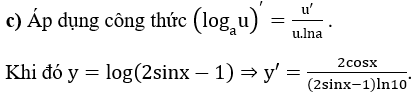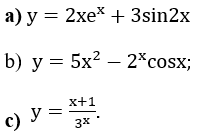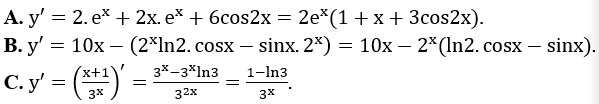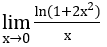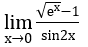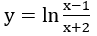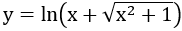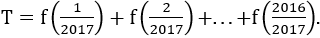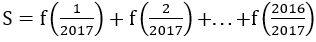Giới Hạn, đạo Hàm Của Hàm Số Mũ, Lũy Thừa, Lôgarit
Có thể bạn quan tâm
Giới hạn, đạo hàm của hàm số mũ, lũy thừa, lôgarit
A. Phương pháp giải & Ví dụ
Bài toán 1: Giới hạn của hàm số mũ, hàm số Logarit
Phương pháp
Chúng ta có các dạng giới hạn đặc biệt sau:
Mở rộng: Ta có
Quy tắc Lopitan: Nếu f(x), g(x) khả vi ở lân cận x0 trừ tại điểm x0 thì:
Đồng thời
Quy tắc vẫn đúng với x → ∞
Bài toán 2: Đạo hàm của các hàm số lũy thừa, hàm số mũ, hàm số logarit
Phương pháp:
- Hàm số lũy thừa:
Hàm số y = xα, (α ∈ R) có đạo hàm với mọi x > 0 và (xα)' = α.xα-1.
- Hàm số mũ:
- Hàm số Logarit:
Ví dụ minh họa
Bài 1: Tìm các giới hạn sau:
Hướng dẫn:
a) Ta biến đổi
b) Ta biến đổi
c) Ta biến đổi
Bài 2: Tính đạo hàm của các hàm số sau:
Hướng dẫn:
Bài 3: Tính đạo hàm của các hàm số sau:
Hướng dẫn:
B. Bài tập vận dụng
Bài 1: Tìm giới hạn sau
Bài 2: Tìm giới hạn sau
Bài 3: Tính đạo hàm của hàm số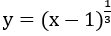 
tại điểm x = 2
Bài 4: Tính đạo hàm của hàm số y = log(ln2x).
Bài 5: Tính đạo hàm của hàm số
Bài 6: Tính đạo hàm của hàm số
Bài 7: Tính đạo đạo hàm của hàm số y=log3(x+1)-2ln(x-1)+2x tại điểm x = 2
Bài 8: Cho hàm số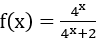 
. Tính tổng T
Bài 9: Cho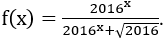 
. Tính giá trị biểu thức S
Bài 10: Cho hàm số y = ln(2x2 + e2). Nếu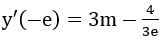 
thì giá trị m bằng bao nhiêu?
Từ khóa » Giới Hạn Hàm Ln
-
Giới Hạn, đạo Hàm Của Hàm Số Mũ, Lũy Thừa, Lôgarit
-
Giới Hạn, đạo Hàm Của Hàm Số Mũ, Lũy Thừa, Lôgarit - Toán Lớp 12
-
[PDF] Bảng Các Công Thức Tính Giới Hạn Hàm Số - Boxthuthuat
-
Chủ đề 5: Giới Hạn, đạo Hàm Của Hàm Số Mũ, Lũy Thừa, Lôgarit
-
Phương Pháp Logarit Hoá - Giới Hạn Lũy Thừa Mũ (#1) - YouTube
-
Tính Giới Hạn Liên Quan đến Hàm Số Mũ Và Hàm Số Logarit
-
Tính Giới Hạn Và đạo Hàm Của Hàm Số Mũ - Logarit
-
Hàm Số Mũ - Lý Thuyết Toán 12
-
Ước Tính Bằng Cách Sử Dụng Quy Tắc Quy Tắc L'Hôpital Giới Hạn ...
-
Biểu Thị Giới Hạn Khi X Tiến Dần đến 0 Của ( Log Tự Nhiên Của 1+x)/x
-
Các Phương Pháp Tính Giới Hạn Hàm Số Biên Soạn Đặng Nhật
-
Hàm Số Mũ Và Hàm Số Logarit
-
Công Thức Giới Hạn Của Hàm Số Mũ | Dương Lê