Hàm Bậc Nhất – Đường Thẳng

Trang chủ » Cách Vẽ Pt đường Thẳng » Hàm Bậc Nhất – Đường Thẳng

Có thể bạn quan tâm

Skip to content

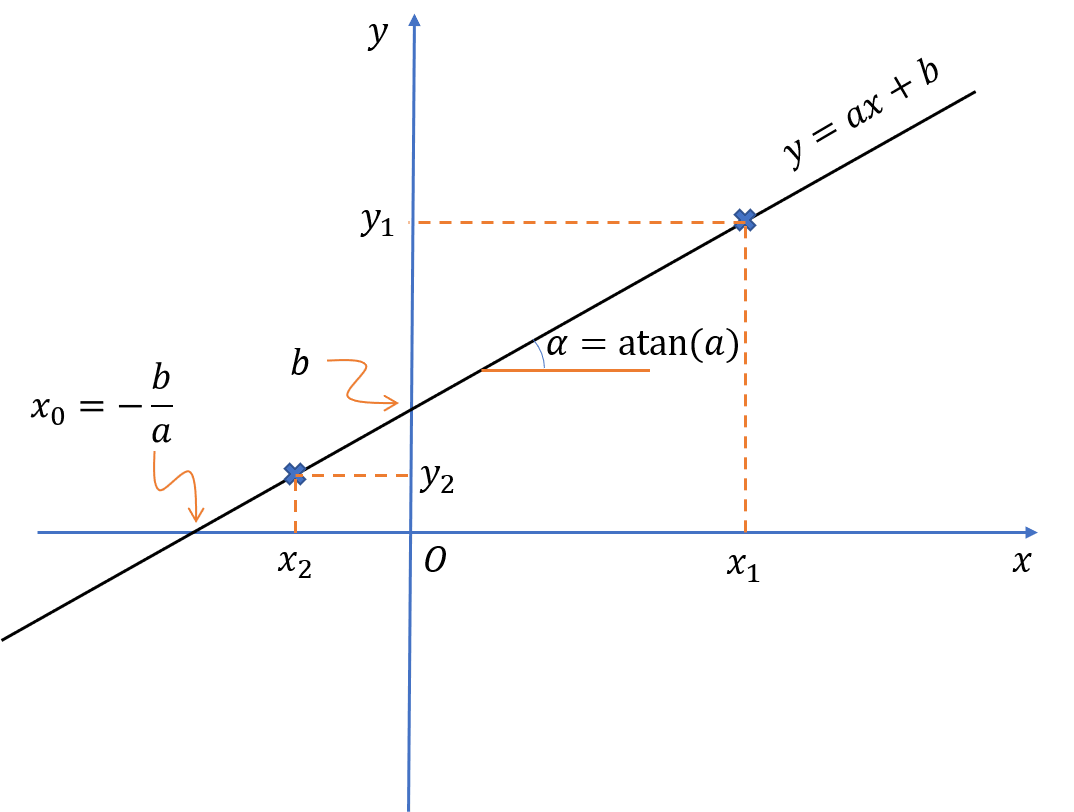
Xét một đường thẳng trong hệ trục tọa độ Oxy như hình vẽ trên.

Phương trình dạng chuẩn hóa của đường thẳng này là:

\(y=ax+b\)

Dạng tổng quát của phương trình này có dạng:

\(Ax + By + C = 0\)

Nếu \(x=0\) thì \(y = b\). Nói cách khác, đường thẳng này cắt trục tung tại điểm có tung độ bằng \(b\). Vì vậy \(b\) được gọi là tung độ gốc của đường thẳng.

Nếu \(y=0\) thì \(x = -b/a\). Nghĩa là đường thẳng cắt trục hoành tại điểm có hoành độ bằng \(-b/a\). Đây cũng chính là nghiệm của phương trình:

\(ax+b=0\)

Góc nghiêng \(\alpha\) của đường thẳng so với đường nằm ngang có độ dốc là:

\(tan(\alpha) = a\)

vì vậy \(a\) còn được gọi là hệ số góc của đường thẳng. Ngoài ra, \(a\) cũng là đạo hàm của phương trình đường thẳng \(y=ax+b\).

Giả sử hai điểm có tọa độ là \((x_1, y_1)\) và \((x_2, y_2)\) đều nằm trên đường thẳng thì độ dốc của đường thẳng có thể được xác định bằng:

\(a = (y_2 – y_1)/(x_2 – x_1)\)

Nó chính bằng độ chênh cao (tức là \(y_2 – y_1)\) chia cho khoảng cách theo phương ngang (bằng với \(x_2 – x_1)\).

Phương trình đường thẳng đi qua điểm \((x_1, y_1)\) và có hệ số góc (độ dốc) là \(a\) có thể được viết là:

\(y-y_1 = a(x-x_1)\)

Khoảng cách giữa hai điểm có tọa độ \((x_1, y_1)\) và \((x_2, y_2)\) là:

\(d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)

Thực ra đây là kết quả của việc áp dụng định lý Pythagoras vào tam giác vuông thôi. Tự suy nghĩ thử nhé.

Leave a Reply Cancel reply

You must be logged in to post a comment.

error: Content is protected !!
  • Have an account? Log In
Login Name: Password: Remember Me

Từ khóa » Cách Vẽ Pt đường Thẳng