Hàm đệ Quy Trong C

1.Hàm đệ quy là gì?

Đệ quy là quá trình lặp lại các mục theo cách tương tự. Trong ngôn ngữ lập trình, một hàm được coi là hàm đệ quy nếu như có sự gọi lại của chính hàm đó ngay bên trong chính nó.

Khi sử dụng hàm đệ quy ta cần quan tâm đến việc điều kiện thoát khỏi hàm, nếu không có điều kiện này hàm này sẽ thực hiện vô hạn và giống như vòng lặp vô hạn chương trình này sẽ gây ra hiện tượng giật, lag, tràn bộ nhớ khi được thực thi.

Các hàm đệ quy rất hữu ích để giải quyết nhiều vấn đề toán học, chẳng hạn như tính giai thừa của một số, tạo chuỗi Fibonacci, v.v.

Cấu trúc của hàm đệ quy như sau:

void recursion() {     //goi lai chinh ban than recursion();  }

Trong đó:

• Void là kiểu trả về của hàm (tùy vào bài toán mà sẽ có kiểu trả về khác nhau)
• Recursion là tên hàm đệ quy (tên hàm có thể đặt bất kỳ theo ý muốn)

Một cách nhìn trực quan nhất về hàm đệ quy trong lập trình:

2.Tính giai thừa của một số sử dụng đệ quy

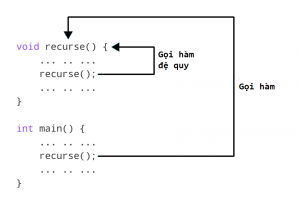
Chương trình dưới đây thực hiện việc tính giai thừa của một số thông qua sử dụng hàm đệ quy.

#include <stdio.h> int giaithua(int n) { //neu n bang 0 hoac n bang 1 thi n! = 1 if(n == 0 || n == 1) { return 1; } //goi lai ham tinh gia thua theo cong thuc n! = n * (n-1)! return n * giaithua(n - 1); } int main() { //khai bao n int n; printf("Nhap N: "); scanf("%d", &n); printf("%d giai thua la: %d\n", n, giaithua(n)); }

Nhap N: 5 5 giai thua la: 120

Hình dưới đây minh họa việc sử dụng đệ quy cho việc tính n! (ở đây n = 5)

Giải thích:

Vì kết quả của phép tính giai thừa sẽ là một số nguyên nên hàm có kiểu trả về là int.

Như ta đa biết, n! (n giai thừa) được tính theo công thức n! = n * (n-1)! và khi tính giai thừa người ta quy ước 0! = 1 và 1! = 1 quy ước này chính là điều kiện dừng của hàm đệ quy tính n giai thừa ở chương trình trên!

Điều kiện return 1; ở trên là hết sức cần thiết, nó phải được đặt ở đầu hàm để thực hiện kiểm tra trước khi hàm đệ quy có sự gọi lại chính nó.

3.Tính chuỗi số Fibonacci sử dụng đệ quy

Chuỗi số Fibonacci được tính theo công thức: f(n) = f(n-1) + f(n-2) (công thức này đúng khi n > 2). Trong dãy Fibonacci người ta cũng quy ước rằng f(1) = 1 và f(2) = 1

Chương trình sử dụng đệ quy để tính dãy Fibonacci trong khoảng từ 1 đến n (ở đây n do người dùng nhập vào):

#include <stdio.h> int fibonacci(int n) { //dieu kien dung cua fibonacci if(n == 0) { return 0; } if(n == 1) { return 1; } //tinh ket qua chuoi fibonacci theo f(n) = f(n-1) + f(n-2) return fibonacci(n-1) + fibonacci(n-2); } int main() { int n; printf("Nhap N: "); scanf("%d", &n); printf("Ket qua chuoi FIBONACCI tu 0 den %d la: \n", n); //duyet cac so tu 0 den n va dua vao ham fibonacci de nhan ket qua for (int i = 0; i < n; i++) { printf("%d \n", fibonacci(i)); } }

Nhap N: 5 Ket qua chuoi FIBONACCI tu 0 den 5 la: 0 1 1 2 3

Minh họa chương trình trên với dạng cây:

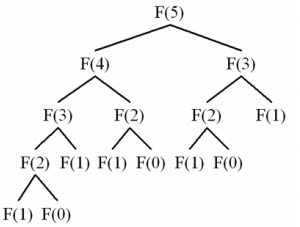
Giải thích:

Hàm Fibonacci cũng trả về một kết quả là số nguyên nên ta cũng có kiểu tra về là int.

Trong hàm ta có điều kiện dừng khi n = 0 thì sẽ return 0 hoặc khi n = 1 thì sẽ return 1. Đây chính là điều kiện kết thúc hàm đệ quy trong bài toán này!

Câu lệnh return fibonacci(n-1) + fibonacci(n-2); chính là việc thực hiện phép tính f(n) = f(n-1) + f(n-2)

Chú ý: Số lượng tính toán sẽ tăng gấp đôi trên mỗi lần gọi đệ quy, vì vậy khi nhập N quá lớn chương trình sẽ cần phải tốn một lượng thời gian để tính toán đưa ra kết quả!