Hàm Mũ – Wikipedia Tiếng Việt

Trang chủ » Hàm Số Mũ Và Logarit Là Gì » Hàm Mũ – Wikipedia Tiếng Việt

Có thể bạn quan tâm

Một phần của loạt bài về
hằng số toán học e
Tính chất
  • Logarit tự nhiên
  • Hàm mũ
Ứng dụng
  • Lãi kép
  • Đồng nhất thức Euler
  • Công thức Euler
  • Chu kỳ bán rã
Định nghĩa e
  • Vô tỉ
  • Biểu diễn của e
  • Định lý Lindemann–Weierstrass
Con người
  • John Napier
  • Leonhard Euler
Chủ đề liên quan
  • Giả thuyết Schanuel
  • x
  • t
  • s

Trong toán học, hàm mũ là hàm số có dạng y = ax, với cơ số a là số dương khác 1.

Tính chất

[sửa | sửa mã nguồn]
Đồ thị của các hàm số: y = 10x, y = ex, y = 2x, y = (1/2)x (cơ số ghi ngay trên đồ thị tương ứng).
  • Hàm số luôn dương với mọi giá trị của x.
  • Nếu a > 1 hàm đồng biến, 0 < a < 1 hàm nghịch biến.
  • Đồ thị nhận trục hoành làm đường tiệm cận và luôn cắt trục tung tại điểm có tung độ bằng 1.
  • Đạo hàm:
d d x e x = e x . {\displaystyle \,{d \over dx}e^{x}=e^{x}.} d d x e f ( x ) = f ′ ( x ) e f ( x ) . {\displaystyle {d \over dx}e^{f(x)}=f'(x)e^{f(x)}.} d d x a x = a x l n ( a ) . {\displaystyle \,{d \over dx}a^{x}=a^{x}ln(a).} d d x a f ( x ) = f ′ ( x ) a f ( x ) l n ( a ) . {\displaystyle \,{d \over dx}a^{f(x)}=f'(x)a^{f(x)}ln(a).}
  • Hàm mũ luôn có hàm ngược là hàm logarit.

Các công thức đặc biệt

[sửa | sửa mã nguồn]
Đồ thị hàm y = ex (màu xanh) và của chính hàm đó theo phép nội suy Taylor.
  • Từ phép nội suy Taylor người ta tìm được ước lượng như sau:
e x = ∑ n = 0 ∞ x n n ! = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + ⋯ . {\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots .}

Các công thức liên phân số của số Euler

[sửa | sửa mã nguồn]   e x = 1 + x 1 − x x + 2 − 2 x x + 3 − 3 x x + 4 − 4 x x + 5 − 5 x x + 6 − ⋱ {\displaystyle \,\ e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-{\cfrac {4x}{x+5-{\cfrac {5x}{x+6-\ddots }}}}}}}}}}}}} e 2 x / y = 1 + 2 x y − x + x 2 3 y + x 2 5 y + x 2 7 y + x 2 9 y + x 2 11 y + x 2 13 y + ⋱ {\displaystyle e^{2x/y}=1+{\cfrac {2x}{y-x+{\cfrac {x^{2}}{3y+{\cfrac {x^{2}}{5y+{\cfrac {x^{2}}{7y+{\cfrac {x^{2}}{9y+{\cfrac {x^{2}}{11y+{\cfrac {x^{2}}{13y+\ddots \,}}}}}}}}}}}}}}}

Trường hợp đặc biệt khi x = y = 1:

e 2 = 7 + 2 5 + 1 7 + 1 9 + 1 11 + 1 13 + ⋱ . {\displaystyle e^{2}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+{\cfrac {1}{13+\ddots .}}}}}}}}}}}

Mở rộng cho số mũ phức

[sửa | sửa mã nguồn]
Đồ thị dạng quang phổ của hàm z = ex + iy. Hướng từ tối đến sáng theo chiều tăng của trục thực cho thấy hàm số là đơn điệu tăng. Các vạch màu luân phiên tuần hoàn song song với trục thực cho thấy hàm là hàm tuần hoàn.

Người ta đã chứng minh được trong mặt phẳng phức thì công thức ước lượng trên vẫn đúng. Do vậy mọi tính chất của hàm mũ số mũ thực đều đúng trong số mũ phức.

Khi đó, biểu thị:

e x + i y = e x × e i y {\displaystyle e^{x+iy}=e^{x}\times e^{iy}}

Theo công thức Euler ta có: e i y = cos ⁡ y + i sin ⁡ y {\displaystyle e^{iy}=\cos y+i\sin y}

Như vậy: e x + i y = e x ( cos ⁡ y + i sin ⁡ y ) {\displaystyle e^{x+iy}=e^{x}(\cos y+i\sin y)} . Theo đó hàm tuần hoàn theo chu kỳ 2πi.

Tuy nhiên cần lưu ý, phép nâng lũy thừa trong hàm mũ phức không hề giống như mũ thực:

( e z ) w ≠   e ( z w ) {\displaystyle (e^{z})^{w}\not =\ e^{(zw)}}
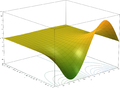  • Đồ thị hàm Z = Im(ex + iy). Đồ thị hàm Z = Im(ex + iy).
  • Đồ thị hàm Z=Module(ex + iy). Đồ thị hàm Z=Module(ex + iy).
  • Đồ thị hàm Z = Re(ex + iy). Đồ thị hàm Z = Re(ex + iy).

Nếu như cơ số cũng là số phức người ta tính như sau:

a b = ( r e θ i ) b = e b ( ln ⁡ r + θ i ) {\displaystyle a^{b}=\left(re^{{\theta }i}\right)^{b}=e^{b(\ln r+{\theta }i)}} .

Xem thêm

[sửa | sửa mã nguồn]
  • Lũy thừa
  • Logarit
  • Hàm mũ hai tầng

Tham khảo

[sửa | sửa mã nguồn]

Từ khóa » Hàm Số Mũ Và Logarit Là Gì