Lý Thuyết Hàm Số Mũ, Hàm Số Lôgarit - Môn Toán - Tìm đáp án, Giải Bài

1. Trang chủ
2. Lớp 12
3. Môn Toán
4. Toán học
5. PHẦN GIẢI TÍCH - TOÁN 12
6. Bài 4. Hàm số mũ, hàm số lôgarit

Lý thuyết hàm số mũ, hàm số lôgarit

1. Định nghĩa

1. Định nghĩa

Hàm số mũ là hàm số có dạng y= ax, hàm số lôgarit là hàm số có dạng  y = logax ( với cơ số a dương khác 1).

2. Tính chất của hàm số mũ y= ax ( a > 0, a# 1).

- Tập xác định: \(\mathbb{R}\).

- Đạo hàm: \(∀x ∈\mathbb{R},y'= a^x \ln a\).

- Chiều biến thiên          

    +) Nếu a> 1 thì hàm số luôn đồng biến

    +) Nếu 0< a < 1 thì hàm số luôn nghịch biến

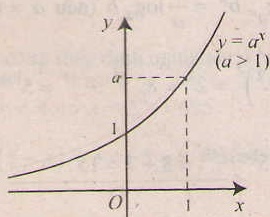
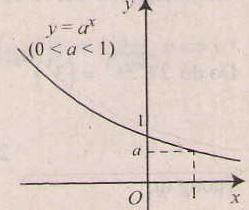
- Tiệm cận: trục Ox là tiệm cận ngang.

- Đồ thị nằm hoàn toàn về phía trên trục hoành (  y= ax  > 0, ∀x), và luôn cắt trục tung tại điểm ( 0;1) và đi qua điểm (1;a).

3. Tính chất của hàm số lôgarit y = logax (a> 0, a# 1).

- Tập xác định: \((0; +∞)\).

- Đạo hàm \(∀x ∈ (0; +∞),y'= \dfrac{1}{x\ln a}\).

- Chiều biến thiên:  

    +) Nếu a> 1 thì hàm số luôn đồng biến

     +) Nếu 0< a < 1 thì hàm số luôn nghịch biến

- Tiệm cận: Trục Oy là tiệm cận đứng.

- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).

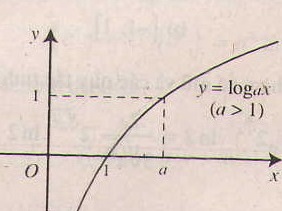
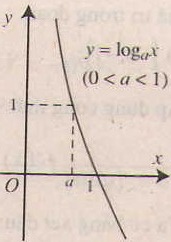
4. Chú ý 

- Nếu \(a > 1\) thì \(\ln a > 0\), suy ra (ax)’ > 0,∀x và (logax)’ > 0, ∀x > 0; 

do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.

Tương tự, nếu \(0 < a< 1\) thì \(\ln a < 0\), (ax)’ < 0 và (logax)’ < 0, ∀x > 0; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.

- Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành

\( (\ln  |x|)'= \dfrac{1}{x}, ∀x \ne 0\) và (loga|x|)’ = \(\dfrac{1}{x \ln a}\), ∀x\(\ne\) 0.

Mẹo Tìm đáp án nhanh nhất Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết hàm số mũ, hàm số lôgarit timdapan.com"

Bài giải tiếp theo

Bài 1 trang 77 SGK Giải tích 12 Bài 2 trang 77 SGK Giải tích 12 Bài 3 trang 77 SGK Giải tích 12 Bài 4 trang 78 SGK Giải tích 12 Bài 5 trang 78 SGK Giải tích 12 Câu hỏi 1 trang 71 SGK Giải tích 12 Câu hỏi 2 trang 71 SGK Giải tích 12 Câu hỏi 3 trang 75 SGK Giải tích 12 Câu hỏi 4 trang 77 SGK Giải tích 12 Các dạng toán về hàm số mũ, hàm số logarit

Bài học bổ sung

Lý thuyết hàm số lũy thừa Lý thuyết lôgarit

Tải sách tham khảo

Xem thêm

Đề khảo sát lần 2 Toán 12 năm 2019 - 2020 trường Bình Xuyên - Vĩnh Phúc

Tải về · 193

Đề thi học sinh giỏi môn Toán lớp 12 năm 2020 - 2021 cấp quốc gia - Đề 13

Tải về · 210

Chuyên đề góc và khoảng cách trong không gian - Nguyễn Nhanh Tiến

Tải về · 161

Đề kiểm tra và đáp án chương 1 môn toán lớp 12 trường THPT thiệu hóa

Tải về · 238

Chuyên đề khối đa diện - Trần Quốc Nghĩa

Tải về · 157

Tài liệu chuyên Toán THPT chuyên đề Hình học không gian

Tải về · 190

Các phương pháp tìm Nguyên hàm - Nguyễn Đình Sỹ

Tải về · 433

Đề kiểm tra hàm số và ứng dụng trường THPT chuyên Ngoại Ngữ - Hà Nội

Tải về · 243

Bài giải liên quan

Lý thuyết hàm số mũ, hàm số lôgarit Bài 1 trang 77 SGK Giải tích 12 Bài 2 trang 77 SGK Giải tích 12 Bài 3 trang 77 SGK Giải tích 12 Bài 4 trang 78 SGK Giải tích 12 Bài 5 trang 78 SGK Giải tích 12 Câu hỏi 1 trang 71 SGK Giải tích 12 Câu hỏi 2 trang 71 SGK Giải tích 12 Câu hỏi 3 trang 75 SGK Giải tích 12 Câu hỏi 4 trang 77 SGK Giải tích 12 Các dạng toán về hàm số mũ, hàm số logarit

Bài học liên quan

Bài 1. Sự đồng biến, nghịch biến của hàm số Bài 2. Cực trị của hàm số Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Bài 4. Đường tiệm cận Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số Bài 1. Lũy thừa Bài 2. Hàm số lũy thừa Bài 3. Lôgarit Bài 4. Hàm số mũ, hàm số lôgarit Bài 5. Phương trình mũ và phương trình lôgarit Bài 6. Bất phương trình mũ và bất phương trình lôgarit Bài 1. Nguyên hàm Bài 2. Tích phân Bài 3. Ứng dụng của tích phân trong hình học. Bài 1. Số phức Bài 2. Cộng, trừ và nhân số phức Bài 3. Phép chia số phức Bài 4. Phương trình bậc hai với hệ số thực Ôn tập Chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm sô Ôn tập Chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit Ôn tập Chương III - Nguyên hàm - Tích phân và ứng dụng Ôn tập Chương IV - Số phức ÔN TẬP CUỐI NĂM - GIẢI TÍCH 12 Đề kiểm tra 15 phút - Chương I - Giải Tích 12 Đề kiểm tra 15 phút - Chương II - Giải Tích 12 Đề kiểm tra 45 phút (1 tiết) - Chương I - Giải Tích 12 Đề kiểm tra 45 phút (1 tiết) - Chương II - Giải Tích 12 Đề kiểm tra 15 phút – Chương IV – Giải tích 12 Đề kiểm tra 45 phút (1 tiết) - Chương IV - Giải Tích 12 Đề kiểm tra 45 phút (1 tiết) - Chương III - Giải Tích 12 Đề kiểm tra 15 phút - Chương III - Giải Tích 12

Từ khóa phổ biến

điều kiện của hàm số mũ hàm số mũ đồ thị hàm logarit điều kiện hàm số mũ hàm số mũ và logarit hàm số logarit hàm mũ hàm logarit hàm số mũ và hàm số logarit hàm số mũ logarit đồ thị hàm số mũ đồ thị hàm số logarit điều kiện logarit điều kiện của logarit hàm số mũ hàm số lôgarit đồ thị hàm mũ đồ thị hàm log ham so mu hàm log so mu đồ thị logarit ham so logarit do thi ham so mu ham mu đồ thị hàm số mũ và logarit ham logarit tính chất của log tính chất logarit mu ln tập xác định của ln toán logarit tính chất của logarit đạo hàm logarit ln là gì og Hỏi bài