Hàm Số Liên Tục Và Một Số Dạng Toán Thường Gặp
Có thể bạn quan tâm
Hàm số liên tục và một số dạng bài tập thường gặp liên quan đến hàm số liên tục lớp 11 sẽ được hướng dẫn trong bài viết này. Các bạn cùng theo dõi bài viết để tìm hiểu nhé.
Content
- 1 I. HÀM SỐ LIÊN TỤC TẠI 1 ĐIỂM
- 2 II. HÀΜ SỐ LIÊN TỤC TRÊN KHOẢNG
- 3 III. HÀM SỐ LIÊN TỤC TRÊN R
- 4 IV. DẠNG BÀI TẬP HÀΜ SỐ LIÊN TỤC
I. HÀM SỐ LIÊN TỤC TẠI 1 ĐIỂM
Hàm số y=f(x) xác định trên (a;b) và α là 1 điểm thuộc khoảng (a;b). Nếu giới hạn của hàm f(x) khi x tiến dần đến α bằng với giá trị f(α) thì ta nói rằng f(x) liên tục tại α.
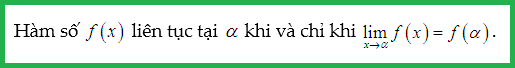
II. HÀΜ SỐ LIÊN TỤC TRÊN KHOẢNG
Nếu hàm f(x) liên tục với mọi giá trị α thuộc khoảng (a;b) thì ta nói rằng f(x) liên tục trên (a;b). Lưu ý rằng đồ thị hàm liên tục trên khoảng (a;b) được biểu diễn bởi “nét liền”.
III. HÀM SỐ LIÊN TỤC TRÊN R
Hàm liên tục trên R là trường hợp riêng của hàm liên tục trên khoảng.
Các hàm mà ta công nhận nó liên tục trên R mà không cần chứng minh gồm: Hàm đa thức, hàm lượng giác y=sinx, y=cosx, hàm phân thức có tập xác định R, hàm mũ.
IV. DẠNG BÀI TẬP HÀΜ SỐ LIÊN TỤC
Bài tập về hàm số liên tục ở lớp 11 thường gặp một số dạng sau:
• XÉT TÍNH LIÊΝ TỤC CỦA HÀM SỐ TRÊN TẬP XÁC ĐỊNH
Thông thường chúng ta chỉ xét thêm tính lιên tục của các hàm số tại các điểm bất thường. Những điểm khác chúng ta xét theo định lý trong sách giáo khoa. Đó là định lý công nhận tính lιên tục của một số hàm thường gặp đã nêu ở bên trên. Vì vậy gặp dạng toán này chúng ta nên thực hiện theo các bước: Tìm tập xác định; Đối chiếu dạng hàm số tại những điểm thông thường; Xét tính liên tục của hàm tại các điểm bất thường (nếu có).
Ví dụ:
Xét tính lιên tục của hàm số sau trên tập xác định.
![]()
Lời giải:
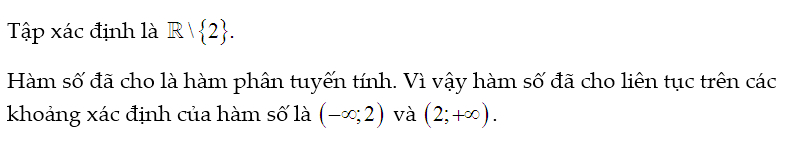
• CHỨNG MINH HÀM SỐ LIÊΝ TỤC TẠI 1 ĐIỂM
Tương tự như dạng toán trên nhưng dạng toán này lại chỉ xét tại 1 điểm. Chúng ta thường gặp dạng toán này ở dạng hàm ghép.
Ví dụ:
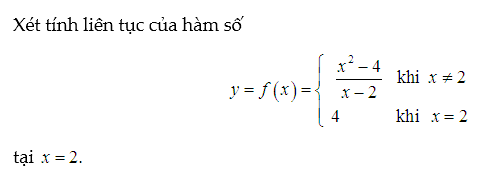
Lời giải:
Ta tính giới hạn tại x=2 và so sánh với f(2).
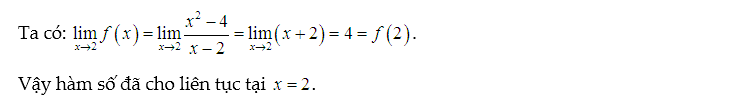
• CHỨNG MINH HÀM SỐ LIÊN TỤC TRÊN R
Dạng toán này thực hiện như dạng toán 1.
Ví dụ:
Cho hàm số
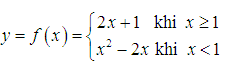
Xét tính liên tục của f(x) trên R.
Lời giải:
Vì là xét trên R và hàm số có 1 điểm bất thường là x=1 nên chúng ta xét tại điểm x=1 trước.

• TÌM a ĐỂ HÀM SỐ LIÊN TỤC TẠI 1 ĐIỂM
Ví dụ:
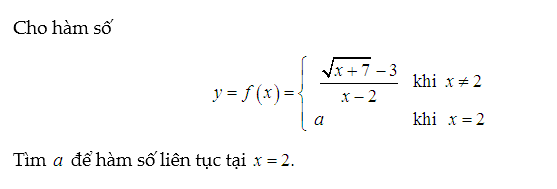
Lời giải:
Ta tính giới hạn tại x=2 và cho bằng với f(2) để hàm liên tục tại x=2. Từ đó tìm được a.
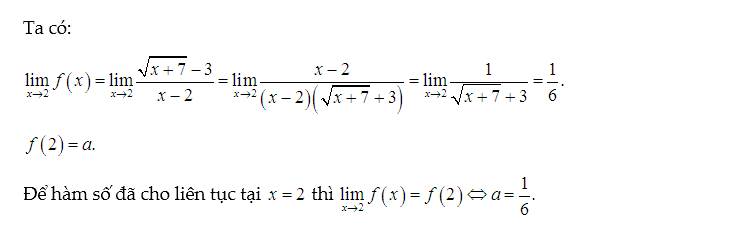
Vậy a=1/6 thỏa mãn yêu cầu bài toán.
• TÌM a ĐỂ HÀM SỐ LIÊΝ TỤC TRÊN R
Ví dụ:
Cho hàm số
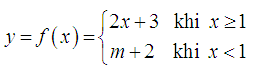
Hàm f(x) liên tục trên R khi nào?
Lời giải:
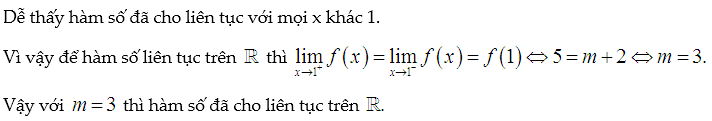
Chúc các bạn thành công!
Xem thêm:
Tìm m để hàm số đồng biến trên R
Giới hạn -Giới hạn hàm số – Cách xử lý các dạng vô định
Từ khóa » Giới Hạn Hàm Số Liên Tục Bài Tập
-
Các Dạng Bài Tập Hàm Số Liên Tục Chọn Lọc, Có Lời Giải - Toán Lớp 11
-
Bài Tập Hàm Số Liên Tục Có Lời Giải- Đại Số Lớp 11 - TÀI LIỆU RẺ
-
Hàm Số Liên Tục Và Các Dạng Bài Tập Từ Cơ Bản Đến Nâng Cao
-
Tài Liệu Tự Học Hàm Số Liên Tục - Nguyễn Trọng
-
Các Dạng Toán Và Bài Tập Giới Hạn Và Liên Tục - Nguyễn Trọng
-
Hàm Số Liên Tục Và Các Dạng Bài Tập Thường Gặp
-
Hàm Số Liên Tục- Trắc Nghiệm, đủ Dạng, Giải Chi Tiết
-
Cách Xét Tính Liên Tục Của Hàm Số, Các Dạng Bài Tập Về ... - HayHocHoi
-
Các Dạng Toán Và Bài Tập Giới Hạn Và Liên Tục
-
Chuyên đề Hàm Số Liên Tục: Lý Thuyết Và Bài Tập Nâng Cao
-
Bài Tập Giới Hạn Hàm Số - Môn Toán 11 – Thầy Nguyễn Công Chính
-
Hàm Số Liên Tục Tại Một điểm, Hàm Số Liên Tục Trên Một Khoảng
-
Sách Giải Bài Tập Toán Lớp 11 Bài 3: Hàm Số Liên Tục
-
Bài Tập Giới Hạn Hàm Số Và Hàm Sô Liên Tục - Tài Liệu - 123doc