Hàm Số Mũ Và Hàm Số Logarit: Định Nghĩa, đạo Hàm, Khảo Sát Hàm ...
Có thể bạn quan tâm
Cùng KhoiA.Vn tìm hiểu hàm số mũ có tập xác định là gì? hàm số mũ có tiệm cận không? Đạo hàm của hàm số mũ tính như thế nào? khảo sát hàm số mũ ra sao? Hàm số logarit có tập xác định là gì? hàm số logarit đồng biến khi nào? có tiệm cận đứng không?...
I. Hàm số mũ
1. Định nghĩa hàm số mũ
- Cho số thực dương α khác 1. Hàm số y = ax được gọi là hàm số mũ cơ số a.
* Ví dụ: Các hàm số mũ là:
y = (√3)x với cơ số là √3;
y = 5x/3 với số mũ là 51/3;
y = 4-x với cơ số là 4-1.
2. Tính chất của hàm số mũ y = ax (0<a≠1)
Tập xác định, Đạo hàm, khoảng đồng biến, nghịch biến và tiệm cận của hàm số mũ.
- Tập xác định: R
- Tập giá trị: (0;+∞)
- Đạo hàm y' = axlna
- Với a>1 hàm số y = ax đồng biến trên R
- Với 0<a<1 hàm số y = ax nghịch biến trên R
- Tiệm cận: Đồ thị hàm số mũ nhận trục hoành Ox làm tiện cận ngang.
- Đồ thị hàm số mũ: Đồ thị nằm hoàn toàn về phía trên trục hoành (y= ax > 0, ∀x), và luôn cắt trục tung tại điểm (o;1) và đi qua điểm (1;a).
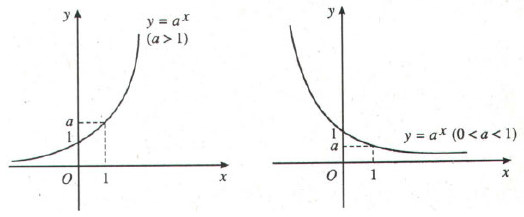 Đồ thị hàm số mũ y = ax
Đồ thị hàm số mũ y = ax
II. Hàm số logarit
1. Định nghĩa hàm số logarit
- Cho số thực dương α khác 1. Hàm số y = logax được gọi là hàm số logarit cơ số a.
* Ví dụ: Các hàm số logarit:
y = log3x với cơ số là 3;
y = log1/4x với cơ số là 1/4;
y = log√5x với cơ số là √5;
y = lnx với cơ số là e;
y = logx với cơ số là 10.
2. Tính chất của hàm số logarit
Tập xác định, Đạo hàm, khoảng đồng biến, nghịch biến và tiệm cận của hàm số logarit.
- Tập xác định: (0;+∞)
- Tập giá trị: R
- Đạo hàm: ∀x ∈ (0;+∞),
- Nếu a>1: y = logax là hàm số đồng biến trên (0;+∞)
- Nếu 0<a<1: y = logax là hàm số đồng biến trên (0;+∞)
- Tiệm cận: Đồ thị hàm số logarit nhận trục tung Oy làm tiện cận đứng.
- Đồ thị hàm số logarit: Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
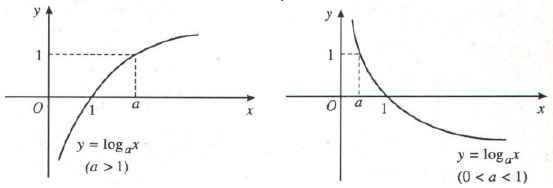 Đồ thị hàm số y = logax
Đồ thị hàm số y = logax
> Chú ý:
Nếu a>1 thì lna>0, suy ra (ax)'>0 và (logax)'>0, ∀x>0;
Do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu 0<a<1 thì lna<0, (ax)'<0 và (logax)'<0, ∀x>0; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.
Từ khóa » Khảo Sát Hàm Số Mũ
-
Bài 4. Hàm Số Mũ, Hàm Số Lôgarit - Củng Cố Kiến Thức
-
Hàm Số Logarit, Hàm Số Mũ: Lý Thuyết & Bài Tập (Kèm Tài Liệu)
-
Hàm Số Mũ Và Hàm Số Lôgarit, Trắc Nghiệm Toán Học Lớp 12
-
Đồ Thị Hàm Số Mũ Và Logarit - đầy đủ Lý Thuyết Và Bài Tập Siêu Chi Tiết
-
Đồ Thị Của Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Logarit
-
Lý Thuyết Và Đồ Thị Của Hàm Số Mũ, Hàm Số Lôgarit - Marathon
-
Lý Thuyết Hàm Số Mũ, Hàm Số Lôgarit | SGK Toán Lớp 12
-
Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Lôgarit - Nguyễn Tài Chung
-
Phân Loại Câu Hỏi Chuyên đề Khảo Sát Hàm Số Và Mũ - Lê Minh Cường
-
Bài Tập Nâng Cao Khảo Sát Hàm Số, Phương Trình Mũ & Logarit
-
Hàm Số Mũ - Tỷ Mỷ Làm Toán. Độc Lập Suy Nghĩ.
-
Đồ Thị Hàm Số Mũ Và Logarit - Toán Lớp 12 - Thầy Nguyễn Quốc Chí
-
Giải Toán 12: Bài 4. Hàm Số Mũ Và Hàm Số Lôgarit - Giải Bài Tập
-
Hàm Số Mũ Và Logarit