Hãy Chứng Minh định Lí Pom-piu : Ở Miền Trong 1 Tam Giác đều, Cứ ...

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng

• Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn

Đóng Đăng nhập Đăng ký

Lớp học

• Lớp 12
• Lớp 11
• Lớp 10
• Lớp 9
• Lớp 8
• Lớp 7
• Lớp 6
• Lớp 5
• Lớp 4
• Lớp 3
• Lớp 2
• Lớp 1

Môn học

• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Đạo đức
• Tự nhiên và xã hội
• Khoa học
• Lịch sử và Địa lý
• Tiếng việt
• Khoa học tự nhiên
• Hoạt động trải nghiệm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng

• Tất cả
• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Hãy tham gia nhóm Học sinh Hoc24OLM Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Câu hỏi

Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay Nguyễn Tất Đạt 22 tháng 7 2018 lúc 21:23

Hãy chứng minh định lí Pom-piu : Ở miền trong 1 tam giác đều, cứ lấy 1 điểm bất kì thì khoảng cách từ điểm đó đến 3 đỉnh của tam giác thỏa mãn độ dài 3 cạnh của 1 tam giác ?

Lớp 7 Toán Những câu hỏi liên quan

• Lê Song Phương
• 

27 tháng 12 2021 lúc 17:22

Hãy chứng minh rằng: Với một tam giác đều cố định và một điểm bất kì nằm trong tam giác đều đó thì tổng các khoảng cách từ điểm đó đến 3 cạnh của tam giác đều là không đổi.

Xem chi tiết Lớp 9 Toán Câu hỏi của OLM 1 0 Gửi Hủy Nguyễn Nam Dương 27 tháng 12 2021 lúc 17:20

Xét tam giác ABC, M là điểm trong tam giác, MD,ME,MF lần lượt là hình chiếu của M lên AB,AC,BC

Kẻ đường cao AH const

Đặt \(AB=AC=BC=a\)

\(S_{ABC}=S_{AMB}+S_{AMC}+S_{BMC}\)

\(=\frac{1}{2}\left(DM.AB+ME.AC+MF.BC\right)\)

\(=\frac{1}{2}a\left(DM+ME+MF\right)\)

\(=\frac{1}{2}a.AH\)

\(=DM+ME+MF=AH\left(đpcm\right)\)

Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy

• Rhider
• 

27 tháng 12 2021 lúc 17:10

Cop mạng cũng đc 

tick hết

Hãy chứng minh rằng: Với một tam giác đều cố định và một điểm bất kì nằm trong tam giác đều đó thì tổng các khoảng cách từ điểm đó đến 3 cạnh của tam giác đều là không đổi.

Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Nguyễn Hoàng Minh 27 tháng 12 2021 lúc 17:14

Xét tam giác ABC, M là điểm trong tam giác, MD,ME,MF lần lượt là hình chiếu của M lên AB,AC,BC

Kẻ đường cao \(AH\) const

Đặt \(AB=AC=BC=a\)

\(S_{ABC}=S_{AMB}+S_{AMC}+S_{BMC}\\ =\dfrac{1}{2}\left(DM.AB+ME.AC+MF.BC\right)\\ =\dfrac{1}{2}a\left(DM+ME+MF\right)\\ =\dfrac{1}{2}a.AH\\ \Rightarrow DM+ME+MF=AH\\ \RightarrowĐpcm\)

Đúng 1 Bình luận (0) Gửi Hủy

• Đốc Trần Khánh Uyến 66

25 tháng 11 2018 lúc 19:44

Chứng minh rằng: Tổng khoảng cách từ một điểm bất kì trong tam giác đều đến 3 cạnh của một tam giác không phụ thuộc vào vị trí điểm đó trong tam giác

Xem chi tiết Lớp 8 Toán Câu hỏi của OLM 0 0 Gửi Hủy

• Phạm Bá Gia Nhất

12 tháng 2 2019 lúc 19:52

chứng minh rằng tổng các khoảng cách từ 1 điểm bất kì trog tam giác đều đến 3 cạnh của tam giác k phụ thuộc vào vị trí của điểm đó

 

Xem chi tiết Lớp 8 Toán Câu hỏi của OLM 0 0 Gửi Hủy

• Minh Hiền
• 

16 tháng 8 2015 lúc 16:16

Cho tam giác đều ABC và 1 điểm M bất kì. CMR: trong 3 đoạn thẳng MA, MB, MC, mỗi đoạn thẳng không lớn hơn tổng của 2 đoạn thẳng kia ( định lí Pom-piu)

Xem chi tiết Lớp 7 Toán Câu hỏi của OLM 2 0 Gửi Hủy A Toi Mua 16 tháng 8 2015 lúc 16:16

M∈ nửa mặt phẳng bờ AC không chứa B.-Kẻ tia Cx sao cho tia Cx tạo với đoạn BC một góc bằng góc ACMˆ.-Trên Cx lấy E sao cho CE=CM(1), ta được hình trênDễ dàng CM: BM+MC>MA, BM+MA>MC (Bạn nào muốn CM thì áp dụng tính chất cạnh và góc trong một tam giác)Bây giờ ta sẽ chứng minh MA+MC≥MBCM:ΔBEC=ΔAMC(c.g.c)⇒BE=AM(2)Ta có:BCEˆ=MCAˆ(ΔBEC=ΔAMC)(3)Mà: BCEˆ+ACEˆ=60o(4)Từ (1), (3), (4):⇒ΔECM đều⇔MC=ME(5)Theo bất đẳng thức trong một tam giác, ta có:BE+ME>BM(6)Từ (2), (5), (6):⇒MA+MC≥MBDấu '=' xảy ra khi;MA=MC

Đúng 0 Bình luận (0) Gửi Hủy Lê Phương Anh 14 tháng 7 2018 lúc 14:27

Cho M nằm trong tam giác đều ABC chứng minh 1 trong 3 đoạn thẳng MA ,MB ,MC nhỏ hơn tổng 2 đoạn thẳng còn lại

Đúng 0 Bình luận (0) Gửi Hủy

• Vương Tuấn Khải

9 tháng 4 2015 lúc 20:13

chứng minh: Điểm cách đều 3 đỉnh của một tam giac vuông là trung điểm của cạnh huyền của tam giác đó.

Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.

Xem chi tiết Lớp 7 Toán Câu hỏi của OLM 0 0 Gửi Hủy

• linh ngoc

2 tháng 8 2018 lúc 21:22

Cho tam giác đều ABC cạnh là a và M là một điểm bất kì nằm trong tam giác ABC. Chứng minh rằng tổng khoảng cách từ M đến 3 cạnh của tam giác ABC không phụ thuộc vào vị trí của M.

Xem chi tiết Lớp 7 Toán Câu hỏi của OLM 0 0 Gửi Hủy

• Nguyễn Thị Thanh Thảo
• 

1 tháng 4 2015 lúc 17:29

Chứng minh  rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.

Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.

Xem chi tiết Lớp 7 Toán Câu hỏi của OLM 1 0 Gửi Hủy Lê Qúy Dương 29 tháng 3 2016 lúc 19:31

bài 66 trang 49 sách bài tập toán lớp 7

Đúng 0 Bình luận (0) Gửi Hủy

• Pham Trong Bach

24 tháng 5 2017 lúc 12:30

Sử dụng bài 55 để chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.

Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.

Xem chi tiết Lớp 7 Toán 1 0 Gửi Hủy Cao Minh Tâm 24 tháng 5 2017 lúc 12:30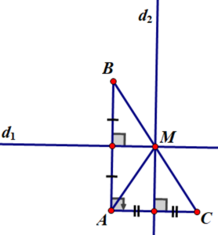

+ Giả sử ∆ABC vuông tại A.

d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.

d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.

+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.

QUẢNG CÁO

+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)

+ M là trung điểm của cạnh BC (đpcm)

*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC

⇒ MB = MC = BC/2

Mà MA = MB = MC (cmt)

⇒ MA = BC/2

Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.

Đúng 0 Bình luận (0) Gửi Hủy

Khoá học trên OLM (olm.vn)

• Toán lớp 7 (Kết nối tri thức với cuộc sống)
• Toán lớp 7 (Cánh Diều)
• Toán lớp 7 (Chân trời sáng tạo)
• Ngữ văn lớp 7 (Kết nối tri thức với cuộc sống)
• Ngữ văn lớp 7 (Cánh Diều)
• Ngữ văn lớp 7 (Chân trời sáng tạo)
• Tiếng Anh lớp 7 (i-Learn Smart World)
• Tiếng Anh lớp 7 (Global Success)
• Khoa học tự nhiên lớp 7 (Kết nối tri thức với cuộc sống)
• Khoa học tự nhiên lớp 7 (Cánh diều)
• Khoa học tự nhiên lớp 7 (Chân trời sáng tạo)
• Lịch sử và địa lý lớp 7 (Kết nối tri thức với cuộc sống)
• Lịch sử và địa lý lớp 7 (Cánh diều)
• Lịch sử và địa lý lớp 7 (Chân trời sáng tạo)
• Giáo dục công dân lớp 7 (Kết nối tri thức với cuộc sống)
• Giáo dục công dân lớp 7 (Cánh diều)
• Giáo dục công dân lớp 7 (Chân trời sáng tạo)