Hệ Phương Trình đối Xứng Loại 1
Có thể bạn quan tâm
Bài viết hướng dẫn nhận dạng và cách giải hệ phương trình đối xứng loại 1 cùng các bài toán có liên quan đến hệ phương trình đối xứng loại 1.
I. LÝ THUYẾT CẦN NẮM 1. Định nghĩa: Hệ phương trình đối xứng loại 1 là hệ phương trình có dạng $\left\{ \begin{array}{l} f\left( {x;y} \right) = a\\ g\left( {x;y} \right) = b \end{array} \right.$ $\left( I \right)$ trong đó $f\left( {x;y} \right)$, $g\left( {x;y} \right)$ là các biểu thức đối xứng, tức là $f\left( {x;y} \right) = f\left( {y;x} \right)$, $g\left( {x;y} \right) = g\left( {y;x} \right).$ 2. Cách giải hệ phương trình đối xứng loại 1: + Đặt $S=x+y$, $P=xy.$ + Biểu diễn $f(x;y)$, $g(x;y)$ qua $S$ và $P$, ta có hệ phương trình: $\left\{ \begin{array}{l} F\left( {S;P} \right) = 0\\ G\left( {S;P} \right) = 0 \end{array} \right.$, giải hệ phương trình này ta tìm được $S$, $P.$ + Khi đó $x$, $y$ là nghiệm của phương trình ${X^2} – SX + P = 0$ $(1).$ 3. Một số biểu diễn biểu thức đối xứng qua $S$ và $P$: ${x^2} + {y^2}$ $ = {\left( {x + y} \right)^2} – 2xy$ $ = {S^2} – 2P.$ ${x^3} + {y^3}$ $ = \left( {x + y} \right)\left( {{x^2} + {y^2} – xy} \right)$ $ = {S^3} – 3SP.$ ${x^2}y + {y^2}x$ $ = xy\left( {x + y} \right) = SP.$ ${x^4} + {y^4}$ $ = {\left( {{x^2} + {y^2}} \right)^2} – 2{x^2}{y^2}$ $ = {\left( {{S^2} – 2P} \right)^2} – 2{P^2}.$ 4. Chú ý: + Nếu $(x;y)$ là nghiệm của hệ $(I)$ thì $(y;x)$ cũng là nghiệm của hệ $(I).$ + Hệ $(I)$ có nghiệm khi $(1)$ có nghiệm hay ${S^2} – 4P \ge 0.$
II. VÍ DỤ MINH HỌA Ví dụ 1. Giải các hệ phương trình sau: 1. $\left\{ \begin{array}{l} x + y + 2xy = 2\\ {x^3} + {y^3} = 8 \end{array} \right.$ 2. $\left\{ \begin{array}{l} {x^3} + {y^3} = 19\\ \left( {x + y} \right)\left( {8 + xy} \right) = 2 \end{array} \right.$
1. Đặt $S = x + y$, $P = xy$. Khi đó hệ phương trình đã cho trở thành: $\left\{ \begin{array}{l} S + 2P = 2\\ S\left( {{S^2} – 3P} \right) = 8 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} P = \frac{{2 – S}}{2}\\ S\left( {{S^2} – \frac{{6 – 3S}}{2}} \right) = 8 \end{array} \right.$ $ \Rightarrow 2{S^3} + 3{S^2} – 6S – 16 = 0$ $ \Leftrightarrow \left( {S – 2} \right)\left( {2{S^2} + 7S + 8} \right) = 0$ $ \Leftrightarrow S = 2 \Rightarrow P = 0.$ Suy ra $x$, $y$ là nghiệm của phương trình: ${X^2} – 2X = 0$ $ \Leftrightarrow \left[ \begin{array}{l} X = 0\\ X = 2 \end{array} \right.$ Vậy nghiệm của hệ phương trình đã cho là: $\left\{ \begin{array}{l} x = 0\\ y = 2 \end{array} \right.$ hoặc $\left\{ \begin{array}{l} x = 2\\ y = 0 \end{array} \right.$ 2. Đặt $S=x+y$, $P=xy$. Khi đó hệ phương trình đã cho trở thành: $\left\{ \begin{array}{l} S\left( {{S^2} – 3P} \right) = 19\\ S\left( {8 + P} \right) = 2 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} SP = – 8S\\ {S^3} – 3\left( {2 – 8S} \right) = 19 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} SP = 2 – 8S\\ {S^3} + 24S – 25 = 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} S = 1\\ P = – 6 \end{array} \right.$ Suy ra $x$, $y$ là nghiệm của phương trình ${X^2} – X – 6 = 0$ $ \Leftrightarrow \left[ \begin{array}{l} X = 3\\ X = – 2 \end{array} \right.$ Vậy hệ phương trình đã cho có cặp nghiệm: $(x;y)=(-2;3),(3;-2).$
Ví dụ 2. Giải các hệ phương trình sau: 1. $\left\{ \begin{array}{l} 2\left( {x + y} \right) = 3\left( {\sqrt[3]{{{x^2}y}} + \sqrt[3]{{x{y^2}}}} \right)\\ \sqrt[3]{x} + \sqrt[3]{y} = 6 \end{array} \right.$ 2. $\left\{ \begin{array}{l} x + y + \frac{1}{x} + \frac{1}{y} = 4\\ {x^2} + {y^2} + \frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} = 4 \end{array} \right.$
1. Đặt $a = \sqrt[3]{x}$, $b = \sqrt[3]{y}$. Khi đó hệ phương trình đã cho trở thành: $\left\{ \begin{array}{l} 2\left( {{a^3} + {b^3}} \right) = 3\left( {{a^2}b + {b^2}a} \right)\\ a + b = 6 \end{array} \right.$ Đặt $S=a+b$, $P=ab$, ta được: $\left\{ \begin{array}{l} 2\left( {{S^3} – 3SP} \right) = 3SP\\ S = 6 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} 2\left( {36 – 3P} \right) = 3P\\ S = 6 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} S = 6\\ P = 8 \end{array} \right.$ Suy ra $a$, $b$ là nghiệm của phương trình: ${X^2} – 6X + 8 = 0$ $ \Leftrightarrow \left[ \begin{array}{l} X = 2\\ X = 4 \end{array} \right.$ Suy ra: $\left\{ \begin{array}{l} a = 2 \Rightarrow x = 8\\ b = 4 \Rightarrow y = 64 \end{array} \right.$ hoặc $\left\{ \begin{array}{l} a = 4 \Rightarrow x = 64\\ b = 2 \Rightarrow y = 8 \end{array} \right.$ Vậy nghiệm của hệ phương trình đã cho là: $\left( {x;y} \right) = \left( {8;64} \right),\left( {64;8} \right).$ 2. Đặt $a = x + \frac{1}{x}$ $b = y + \frac{1}{y}$, ta có hệ phương trình: $\left\{ \begin{array}{l} a + b = 4\\ {a^2} + {b^2} – 4 = 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a + b = 4\\ {\left( {a + b} \right)^2} – 2ab = 8 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a + b = 4\\ ab = 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = 2\\ b = 2 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x + \frac{1}{x} = 2\\ y + \frac{1}{y} = 2 \end{array} \right.$ $ \Leftrightarrow x = y = 1.$ Vậy hệ phương trình đã cho có nghiệm $x=y=1.$
Ví dụ 3. Giải các hệ phương trình sau: 1. $\left\{ \begin{array}{l} \sqrt {{x^2} + {y^2}} + \sqrt {2xy} = 8\sqrt 2 \\ \sqrt x + \sqrt y = 4 \end{array} \right.$ 2. $\left\{ \begin{array}{l} x + y – \sqrt {xy} = 3\\ \sqrt {x + 1} + \sqrt {y + 1} = 4 \end{array} \right.$
1. Điều kiện: $x,y \ge 0.$ Đặt $t = \sqrt {xy} \ge 0$, ta có: $xy = {t^2}$ và từ $\sqrt x + \sqrt y = 4$ $ \Rightarrow x + y = 16 – 2t.$ Thế vào phương trình thứ nhất của hệ phương trình, ta được: $\sqrt {{t^2} – 32t + 128} = 8 – t$ $ \Leftrightarrow \left\{ \begin{array}{l} t \le 8\\ {t^2} – 32t + 128 = {\left( {t – 8} \right)^2} \end{array} \right.$ $ \Leftrightarrow t = 4.$ Suy ra: $\left\{ \begin{array}{l} xy = 16\\ x + y = 8 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = 4\\ y = 4 \end{array} \right.$ Vậy hệ phương trình đã cho có nghiệm: $x=y=4.$ 2. Điều kiện: $\left\{ \begin{array}{l} xy \ge 0\\ x,y \ge – 1 \end{array} \right.$ Đặt $S=x+y$, $P=xy$ ta có: $\left\{ \begin{array}{l} S – \sqrt P = 3\\ S + 2 + 2\sqrt {S + P + 1} = 16 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} S \ge 3;P = {\left( {S – 3} \right)^2}\\ 2\sqrt {S + {{\left( {S – 3} \right)}^2} + 1} = 14 – S \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} 3 \le S \le 14;P = {\left( {S – 3} \right)^2}\\ 4\left( {{S^2} + 8S + 10} \right) = 196 – 28S + {S^2} \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} 3 \le S \le 14;P = {\left( {S – 3} \right)^2}\\ {S^2} + 30S – 52 = 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} S = 6\\ P = 9 \end{array} \right.$ $ \Rightarrow x = y = 3.$ Vậy hệ phương trình đã cho có nghiệm: $(x;y)=(3;3).$
Ví dụ 4. Giải các hệ phương trình sau: 1. $\left\{ \begin{array}{l} \sqrt[4]{{{y^3} – 1}} + \sqrt x = 3\\ {x^2} + {y^3} = 82 \end{array} \right.$ 2. $\left\{ \begin{array}{l} \sqrt {\frac{x}{y}} + \sqrt {\frac{y}{x}} = \frac{7}{{\sqrt {xy} }} + 1\\ \sqrt {{x^3}y} + \sqrt {{y^3}x} = 78 \end{array} \right.$
1. Đặt $u = \sqrt x $ và $v = \sqrt[4]{{{y^3} – 1}}$. Khi đó, hệ phương trình đã cho trở thành: $\left\{ \begin{array}{l} u + v = 3\\ {u^4} + \left( {{v^4} + 1} \right) = 82 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} u + v = 3\\ {u^4} + {v^4} = 81 \end{array} \right.$ $\left( * \right)$ Đặt $S=u+v$, $P=uv$. Với điều kiện ${S^2} – 4P \ge 0$ thì hệ $(*)$ được viết lại: $\left\{ \begin{array}{l} S = 3\\ {S^4} – 4{S^2}P + 2{S^2} = 81 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} S = 3\\ {P^2} – 18P = 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} P = 0\\ S = 3 \end{array} \right.$ hoặc $\left\{ \begin{array}{l} P = 18\\ S = 3 \end{array} \right.$ + Trường hợp 1: Với $S=3$, $P=0$, suy ra $u$, $v$ là nghiệm của phương trình: ${X^2} – 3X = 0$ $ \Leftrightarrow \left[ \begin{array}{l} X = 0\\ X = 3 \end{array} \right.$ Khi đó: $\left\{ \begin{array}{l} u = 0\\ v = 3 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = 0\\ y = \sqrt[3]{{82}} \end{array} \right.$ hoặc $\left\{ \begin{array}{l} u = 3\\ v = 0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = 9\\ y = 1 \end{array} \right.$ + Trường hợp 2: $P=18$, $S=3$ không thỏa mãn điều kiện vì ${S^2} – 4P < 0.$ Vậy hệ phương trình đã cho có nghiệm: $\left( {x;y} \right) = \left( {0;\sqrt[3]{{82}}} \right)$, $\left( {9;1} \right).$ 2. Điều kiện: $xy>0.$ + Trường hợp 1: $x>0$, $y>0$, ta đặt: $u = \sqrt x ,v = \sqrt y .$ + Trường hợp 2: $x<0$, $y<0$, ta đặt: $u = \sqrt { – x} ,v = \sqrt { – y} .$ Cả 2 trường hợp đều đưa về hệ phương trình: $\left\{ \begin{array}{l} \frac{u}{v} + \frac{v}{u} = \frac{7}{{uv}} + 1\\ {u^3}v + {v^3}u = 78 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {u^2} + {v^2} = uv + 7\\ uv\left( {{u^2} + {v^2}} \right) = 78 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {S^2} – 3P = 7\\ P\left( {{S^2} – 2P} \right) = 78 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {S^2} = 3P + 7\\ P\left( {P + 7} \right) = 78 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {S^2} = 3P + 7\\ {P^2} + 7P – 78 = 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} P = 6\\ S = \pm 5 \end{array} \right.$ Từ đó ta tìm được nghiệm của hệ phương trình đã cho là: $(x;y)=(-9;-4),(-4;-9),(4;9)(9;4).$ [ads] Ví dụ 5. Tìm $m$ để các hệ phương trình sau đây có nghiệm: 1. $\left\{ \begin{array}{l} x + y = m\\ {x^2} + {y^2} = 2m + 1 \end{array} \right.$ 2. $\left\{ \begin{array}{l} x + \frac{1}{x} + y + \frac{1}{y} = 5\\ {x^3} + \frac{1}{{{x^3}}} + {y^3} + \frac{1}{{{y^3}}} = 15m – 10 \end{array} \right.$
1. Đặt $S=x+y$, $P=xy$, ta có: $\left\{ \begin{array}{l} S = m\\ {S^2} – 2P = 2m + 1 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} S = m\\ P = \frac{1}{2}\left( {{m^2} – 2m – 1} \right) \end{array} \right.$ Hệ phương trình có nghiệm khi và chỉ khi: ${S^2} – 4P \ge 0$ $ \Leftrightarrow {m^2} – 2\left( {{m^2} – 2m – 1} \right)$ $ = – {m^2} + 4m + 2 \ge 0$ $ \Leftrightarrow 2 – \sqrt 6 \le m \le 2 + \sqrt 6 .$ 2. Đặt $a = x + \frac{1}{x}$, $b = y + \frac{1}{y}$ $ \Rightarrow \left| a \right| \ge 2;\left| b \right| \ge 2.$ Hệ phương trình đã cho trở thành: $\left\{ \begin{array}{l} a + b = 5\\ {a^3} + {b^3} – 3\left( {a + b} \right) = 15m – 10 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a + b = 5\\ ab = 8 – m \end{array} \right.$ Suy ra $a$, $b$ là nghiệm của phương trình: ${X^2} – 5X + 8 – m = 0$ $ \Leftrightarrow {X^2} – 5X + 8 = m$ $(1).$ Hệ phương trình đã cho có nghiệm khi và chỉ khi $(1)$ có hai nghiệm phân biệt thỏa: $\left| X \right| \ge 2.$ Xét tam thức $f\left( X \right) = {X^2} – 5X + 8$ với $\left| X \right| \ge 2$, ta có bảng biến thiên sau:
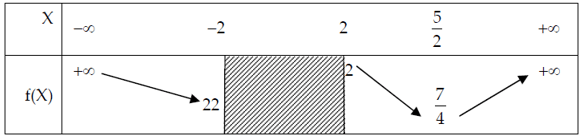
Dựa vào bảng biến thiên suy ra $(1)$ có hai nghiệm thỏa $\left| X \right| \ge 2$ khi và chỉ khi $\left[ \begin{array}{l} m \ge 22\\ \frac{7}{4} \le m \le 2 \end{array} \right.$
Ví dụ 6. Tìm $m$ để hệ phương trình $\left\{ \begin{array}{l} x + y + xy = m\\ {x^2} + {y^2} = m \end{array} \right.$ $(*)$ có nghiệm.
Ta có: $\left( * \right) \Leftrightarrow \left\{ \begin{array}{l} x + y + xy = m\\ {\left( {x + y} \right)^2} – 2xy = m \end{array} \right.$ Đặt $\left\{ \begin{array}{l} S = x + y\\ P = xy \end{array} \right.$, điều kiện ${S^2} \ge 4P$, ta có hệ phương trình: $\left\{ \begin{array}{l} S + P = m\\ {S^2} – 2P = m \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} S + P = m\\ {S^2} + 2S – 3m = 0 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} S = – 1 + \sqrt {1 + 3m} \\ P = m + 1 – \sqrt {1 + 3m} \end{array} \right.\\ \left\{ \begin{array}{l} S = – 1 – \sqrt {1 + 3m} \\ P = m + 1 + \sqrt {1 + 3m} \end{array} \right. \end{array} \right.$ Hệ phương trình đã cho có nghiệm khi và chỉ khi: ${S^2} \ge 4P.$ + Trường hợp 1. Với $\left\{ \begin{array}{l} S = – 1 + \sqrt {1 + 3m} \\ P = m + 1 – \sqrt {1 + 3m} \end{array} \right.$, ta có: ${\left( { – 1 + \sqrt {1 + 3m} } \right)^2}$ $ \ge 4\left( {m + 1 – \sqrt {1 + 3m} } \right)$ $ \Leftrightarrow 2\sqrt {1 + 3m} \ge m + 2$ $ \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} m + 2 \le 0\\ 1 + 3m \ge 0 \end{array} \right.\\ \left\{ \begin{array}{l} m + 2 \ge 0\\ 4\left( {1 + 3m} \right) \ge {\left( {m + 2} \right)^2} \end{array} \right. \end{array} \right.$ $ \Leftrightarrow 0 \le m \le 8.$ + Trường hợp 2. Với $\left\{ \begin{array}{l} S = – 1 – \sqrt {1 + 3m} \\ P = m + 1 + \sqrt {1 + 3m} \end{array} \right.$, ta có: ${\left( { – 1 – \sqrt {1 + 3m} } \right)^2}$ $ \ge 4\left( {m + 1 + \sqrt {1 + 3m} } \right)$ $ \Leftrightarrow 3\sqrt {1 + 3m} \le – m – 2$, dễ thấy bất phương trình này vô nghiệm vì $–m-2<0.$ Vậy hệ phương trình đã cho có nghiệm khi và chỉ khi $0 \le m \le 8.$
Ví dụ 7. Cho $x$, $y$, $z$ là nghiệm của hệ phương trình $\left\{ \begin{array}{l} {x^2} + {y^2} + {z^2} = 8\\ xy + yz + zx = 4 \end{array} \right.$. Chứng minh: $ – \frac{8}{3} \le x,y,z \le \frac{8}{3}.$
Ta có: $\left\{ \begin{array}{l} {x^2} + {y^2} + {z^2} = 8\\ xy + yz + zx = 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {x^2} + {y^2} = 8 – {z^2}\\ xy + z\left( {x + y} \right) = 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {\left( {x + y} \right)^2} – 2xy = 8 – {z^2}\\ xy + z\left( {x + y} \right) = 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {\left( {x + y} \right)^2} – 2\left[ {4 – z\left( {x + y} \right)} \right] = 8 – {z^2}\\ xy + z\left( {x + y} \right) = 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {\left( {x + y} \right)^2} + 2z\left( {x + y} \right) + \left( {{z^2} – 16} \right) = 0\\ xy + z\left( {x + y} \right) = 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x + y = 4 – z\\ xy = {\left( {z – 2} \right)^2} \end{array} \right.$ hoặc $\left\{ \begin{array}{l} x + y = – 4 – z\\ xy = {\left( {z + 2} \right)^2} \end{array} \right.$ Do $x$, $y$, $z$ là nghiệm của hệ phương trình $\left\{ \begin{array}{l} {x^2} + {y^2} + {z^2} = 8\\ xy + yz + zx = 4 \end{array} \right.$ nên: ${\left( {x + y} \right)^2} \ge 4xy$ $ \Leftrightarrow \left[ \begin{array}{l} {\left( {4 – z} \right)^2} \ge 4{\left( {z – 2} \right)^2}\\ {\left( { – 4 – z} \right)^2} \ge 4{\left( {z + 2} \right)^2} \end{array} \right.$ $ \Leftrightarrow – \frac{8}{3} \le z \le \frac{8}{3}.$ Đổi vai trò $x$, $y$, $z$ ta được: $ – \frac{8}{3} \le x,y,z \le \frac{8}{3}.$
Ví dụ 8. Cho hai số thực $x$, $y$ thỏa $x + y = 1$. Tìm giá trị nhỏ nhất của biểu thức: $A = {x^3} + {y^3}.$
Xét hệ phương trình: $\left\{ \begin{array}{l} x + y = 1\\ {x^3} + {y^3} = A \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} S = 1\\ S\left( {{S^2} – 3P} \right) = A \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} S = 1\\ P = \frac{{1 – A}}{3} \end{array} \right.$ Ta có: $x$, $y$ tồn tại $ \Leftrightarrow $ hệ có nghiệm $ \Leftrightarrow {S^2} – 4P \ge 0$ $ \Leftrightarrow 1 – 4\frac{{1 – A}}{3} \ge 0$ $ \Leftrightarrow A \ge \frac{1}{4}.$ Vậy giá trị nhỏ nhất của $A$ là $\min A = \frac{1}{4}$ $ \Leftrightarrow x = y = \frac{1}{2}.$
Ví dụ 9. Cho các số thực $x \ne 0,y \ne 0$ thỏa mãn: $\left( {x + y} \right)xy = {x^2} + {y^2} – xy.$ Tìm giá trị lớn nhất của biểu thức: $A = \frac{1}{{{x^3}}} + \frac{1}{{{y^3}}}.$
Xét hệ phương trình: $\left\{ \begin{array}{l} \left( {x + y} \right)xy = {x^2} + {y^2} – xy\\ \frac{1}{{{x^3}}} + \frac{1}{{{y^3}}} = A \end{array} \right.$ Đặt $a = \frac{1}{x}$, $b = \frac{1}{y}$ $\left( {a,b \ne 0} \right)$, hệ phương trình trên trở thành: $\left\{ \begin{array}{l} a + b = {a^2} + {b^2} – ab\\ {a^3} + {b^3} = A \end{array} \right.$ Đặt $S=a+b$, $P=ab$, ta có: $\left\{ \begin{array}{l} S = {S^2} – 3P\\ S\left( {{S^2} – 3P} \right) = A \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {S^2} = A\\ 3P = {S^2} – S \end{array} \right.$ Từ $a + b = {a^2} + {b^2} – ab > 0$, suy ra $S > 0.$ Hệ phương trình này có nghiệm $ \Leftrightarrow {S^2} \ge 4P$ $ \Leftrightarrow 3{S^2} \ge 4\left( {{S^2} – S} \right)$ $ \Leftrightarrow S \le 4$ $ \Leftrightarrow A = {S^2} \le 16.$ Đẳng thức xảy ra $ \Leftrightarrow \left\{ \begin{array}{l} S = 4\\ P = \frac{{{S^2} – S}}{3} = 4 \end{array} \right.$ $ \Leftrightarrow a = b = 2$ $ \Leftrightarrow x = y = \frac{1}{2}.$ Vậy giá trị lớn nhất của $A$ là $\max A = 16$ $ \Leftrightarrow x = y = \frac{1}{2}.$
Ví dụ 10. Cho $x$, $y$ thỏa mãn $x – 3\sqrt {y + 2} = 3\sqrt {x + 1} – y.$ Tìm giá trị lớn nhất và giá trị nhỏ nhất của $A=x+y.$
Xét hệ phương trình: $\left\{ \begin{array}{l} x – 3\sqrt {y + 2} = 3\sqrt {x + 1} – y\\ x + y = A \end{array} \right.$ Đặt $a = \sqrt {x + 1} $, $b = \sqrt {y + 2} $ $ \Rightarrow a,b \ge 0.$ Hệ phương trình trên trở thành: $\left\{ \begin{array}{l} {a^2} + {b^2} – 3\left( {a + b} \right) – 3 = 0\\ {a^2} + {b^2} = A + 3 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a + b = \frac{A}{3} = S\\ ab = \frac{{{A^2} – 9A – 27}}{{18}} = P \end{array} \right.$ Suy ra hệ phương trình đã cho có nghiệm $ \Leftrightarrow \left\{ \begin{array}{l} S \ge 0\\ P \ge 0\\ {S^2} \ge 4P \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} A \ge 0\\ {A^2} – 9A – 27 \ge 0\\ {A^2} – 18A – 54 \le 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} A \ge 0\\ A \le \frac{{9 – 3\sqrt {21} }}{2} \: hoặc \: A \ge \frac{{9 + 3\sqrt {21} }}{2}\\ 9 – 3\sqrt {15} \le A \le 9 + 3\sqrt {15} \end{array} \right.$ Vậy $\min A = \frac{{9 + 3\sqrt {21} }}{2}$ và $\max A = 9 + 3\sqrt {15} .$
Từ khóa » Bài Tập Hệ đối Xứng Loại 1 Có đáp án
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1 Cực Hay - Toán Lớp 9
-
Bài Tập Hệ đối Xứng Loại 1 Có đáp án | Dương Lê
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1
-
Hệ Phương Trình đối Xứng Loại 1 - Mẹo Giải Nhanh Và Bài Tập Vận Dụng
-
Chuyên đề: Hệ Phương Trình đối Xứng Loại 1
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1 Cực Hay | Toán Lớp 9
-
Bài Tập Về Hệ Phương Trình đối Xứng Loại 1 - 123doc
-
Hệ Phương Trình đối Xứng Loại 1 Và Bài Tập ứng Dụng - TÀI LIỆU RẺ
-
Hệ Phương Trình đối Xứng Loại 1, Cách Giải Và Bài Tập Vận Dụng
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1 Cực Hay
-
Phương Pháp Giải Hệ Đối Xứng Loại 1 - Học Thêm Toán
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1 - Trần Gia Hưng
-
Chuyên đề: Hệ Phương Trình đối Xứng - Toán Cấp 2
-
Hệ Phương Trình đối Xứng Loại 1 – Mẹo Giải Nhanh Và Bài Tập Vận Dụng