Hình Học 7 Bài 1: Hai Góc đối đỉnh - Hoc247

YOMEDIA NONE Trang chủ Toán 7 Chương 1: Đường Thẳng Vuông Góc. Đường Thẳng Song Song Hình học 7 Bài 1: Hai góc đối đỉnh ADMICRO Lý thuyết10 Trắc nghiệm21 BT SGK 214 FAQ

Nội dung bài học sẽ giới thiệu đến các em khái niệm và tính chất của Hai góc đối đỉnh cùng với những dạng bài tập liên quan. Bên cạnh đó là những bài tập có hướng dẫn giải chi tiết sẽ giúp các em nắm được phương pháp giải các bài toán liên quan đề hai góc đối đỉnh.

ATNETWORK

1. Tóm tắt lý thuyết

1.1. Định nghĩa

1.2. Tính chất

2. Bài tập minh hoạ

3. Luyện tập Bài 1 Chương 1 Hình học 7

3.1. Trắc nghiệm về Hai góc đối đỉnh

3.2. Bài tập SGK về Hai góc đối đỉnh

4. Hỏi đáp Bài 1 Chương 1 Hình học 7

Tóm tắt lý thuyết

1.1. Định nghĩa

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của mỗi cạnh góc kia.

1.2. Tính chất

Hai góc đối đỉnh thì bằng nhau \(\widehat {xOy}\) đối đỉnh \(\widehat {x'Oy'} \Rightarrow \widehat {xOy} = \widehat {x'Oy'}\).

Ví dụ 1:

Cho hai đường thẳng xy và zt cắt nhau tại O. Biết góc \(\widehat {xOt}\) lớn gấp 4 lần góc \(\widehat {xOz}\). Tính các góc \(\widehat {xOt},\widehat {tOy},\widehat {xOz}\) và \(\widehat {xOz}.\)

Hướng dẫn giải:

Ta có góc \(\widehat {xOt}\) và \(\widehat {xOz}\) là hai góc kề bù nên \(\widehat {xOt} + \widehat {xOz} = {180^0}\) mà \(\widehat {xOt} = 4\widehat {xOz}\)

Do đó \(4\widehat {xOt} + \widehat {xOz} = {180^0}\,\,\,\,hay\,\,\,\,5\,\,\widehat {xOz}\, = {180^0}\)

Vậy \(\widehat {xOz} = {180^0}:5 = {36^0}\)

Suy ra \(\widehat {xOt} = {4.36^0} = {144^0}\)

Các cặp góc \(\widehat {yOz}\) và \(\widehat {xOt},\,\,\widehat {tOy}\) và \(\widehat {xOz}\) là các cặp góc đổi đỉnh do đó:

\(\begin{array}{l}\widehat {yOz} = \widehat {xOt} = {144^0}\\\widehat {tOy} = \widehat {xOz} = {36^0}\end{array}\)

Ví dụ 2:

Xem các hình a, b, c, d:

Hỏi cặp góc nào đối đỉnh, cặp góc nào không đối đỉnh? Vì sao?

Hướng dẫn giải:

a. Hai góc này không đối đỉnh vì chúng không có đỉnh chung.

b. Hai góc này không đối đỉnh vì mỗi cạnh của góc này không là tia đối của một cạnh của góc kia.

c. Hai góc đối đỉnh vì mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

d. Hai góc này không đối đỉnh vì một cạnh của góc này không là tia đối của cạnh góc kia.

Ví dụ 3:

Ta có: Hai góc không có điểm trong chung là hai góc mà mỗi cạnh góc này không nằm giữa hai cạnh góc kia.

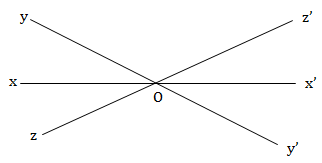
Cho ba đường thẳng phân biệt x’x, y’y, z’z cắt nhau ở điểm O.

a. Hãy tìm 6 cặp góc đối đỉnh.

b. Có bao nhiêu cặp góc đối đỉnh không có điểm trong chung?

Hướng dẫn giải:

a. Có 6 cặp góc đối đỉnh là: \(\widehat {x'Oy'}\) và \(\widehat {xOy\,},\,\widehat {y'Oz'}\) và \(\widehat {yOz},\,\widehat {x'Oz'}\) và \(\widehat {zOx\,},\,\widehat {xOy}\) và \(\widehat {xOy'},\widehat {y'Oz}\) và \(\widehat {yOz'},\widehat {z'Ox}\) và \(\widehat {zOx'}.\)

b. Có ba cặp góc đối đỉnh không có điểm chung trong là: \(\widehat {x'Oy'}\) và \(\widehat {xOy},\widehat {y'Oz}\) và \(\widehat {yOz'},\widehat {z'Ox'}\) và \(\widehat {zOx}.\)

Bài tập minh họa

Bài 1:

Cho \(\widehat {xOy} = {100^0}\) và hai góc \(\widehat {yOz}\) và \(\widehat {xOt}\) cùng kề bù với nó. Hãy xác định hai cặp đối đỉnh và tính số đo của các góc \(\widehat {zOt}\), \(\widehat {xOt}\), \(\widehat {yOz}\).

Hướng dẫn giải:

• Ta có \(\widehat {xOt}\) kề bù với \(\widehat {xOy}\) nên 2 tia Oy, Ot đối nhau.

\(\widehat {yOz}\) kề bù với \(\widehat {xOy}\) nên 2 tia Ox, Oz đối nhau.

Vậy ta được hai cặp góc đối đỉnh là \(\widehat {xOy}\) và \(\widehat {zOt}\); \(\widehat {xOt}\) và \(\widehat {zOy}\).

• Ta có \(\widehat {xOy} = \widehat {zOt} = {100^0}\) (đối đỉnh) và \(\widehat {xOy} + \widehat {yOz} = {180^0}\) (kề bù)

Hay \({100^0} + \widehat {yOz} = {180^0}\)

Suy ra \(\widehat {yOz} = {180^0} - {100^0} = {80^0}\)

Nên \(\widehat {yOz} = \widehat {tOx} = {80^0}\) đối đỉnh

Bài 2:

Cho hai đường thẳng x’x và y’y cắt nhau tại O.

a. Hỏi hai đường thẳng cắt nhau đó tạo thành mấy góc (khác góc bẹt)

b. Tính số đo mỗi góc tạo thành. Nếu biết hiệu số đo của hai góc kề bù là \({30^0}.\)

Hướng dẫn giải:

a. Hai đường thẳng cắt nhau tạo thành 4 góc bẹt: \(xOy,\,\,yOx',\,\,x'Oy'\) và \(y'Ox.\)

b.

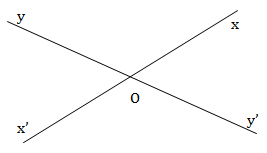
Gọi \(\widehat {xOy}\) và \(\widehat {yOx'}\) là hai góc kề bù.

Giả sử \(\widehat {xOy} - \widehat {yOx'} = {30^0}\)

Lại có \(\widehat {xOy} + \widehat {yOx'} = {180^0}\) (do hai góc kề bù)

\(\begin{array}{l} \Rightarrow 2x\widehat {Oy} = {210^0} \Rightarrow \widehat {xOy} = {150^0}\\ \Rightarrow \widehat {yOx'} = {180^0} - {150^0} = {75^0}\\ \Rightarrow \widehat {xOy'} = \widehat {yOx'} = {75^0}\end{array}\)

Và \(\widehat {x'Oy'} = \widehat {xOy} = {105^0}\) (hai góc đối đỉnh).

Bài 3:

Cho góc bẹt \(\widehat {AOB}\). Trên cùng một nửa mặt phẳng bờ AB, ta vẽ hai tia OC và OD sao cho \(\widehat {AOC} = \widehat {BOD} = {30^0}\)

a. Hai góc \(\widehat {AOC}\) và \(\widehat {BOD}\) có phải là hai góc đối đỉnh không?

b. Vẽ tia OE sao cho tia OB là tia phân giác của góc \(\widehat {DOE}\). Hai góc \(\widehat {AOC}\) và \(\widehat {BOE}\) có phải là hai góc đối đỉnh không?

Hướng dẫn giải:

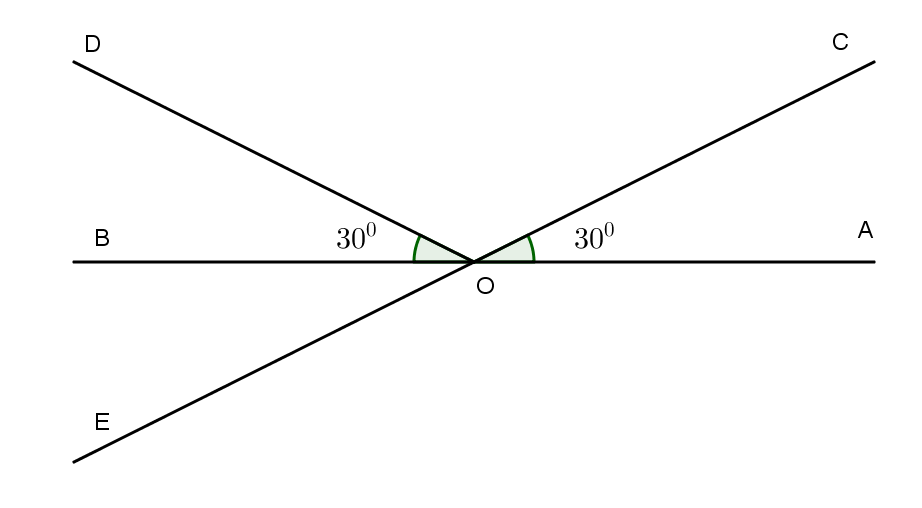
a. Hai góc \(\widehat {AOC}\) và \(\widehat {BOD}\) có một cặp cạnh là hai tia đối nhau, cặp cạnh còn lại không đối nhau nên góc đó không phải là hai góc đối đỉnh.

b. Ta có \(\widehat {AOC} = {30^0}\) nên \(\widehat {BOC} = {150^0}\) (tính chất hai góc kề bù).

Tia OB là tia phân giác của góc \(\widehat {DOE}\) nên \(\widehat {BOD} = \widehat {BOE} = {30^0}\) và tia OD, OE thuộc hai nửa mặt phẳng đối nhau bờ AB.

Suy ra hai tia OC và OE thuộc hai nửa mặt phẳng đối nhau bờ chứa tia OB.

Ta có \(\widehat {BOC} + \widehat {BOE} = {150^0} + {30^0} = {180^0}\)

Suy ra hai tia OC, OE đối nhau.

Hai góc \(\widehat {AOC}\) và \(\widehat {BOE}\) có hai cặp cạnh là hai tia đối nhau nên chúng là hai góc đối đỉnh.

QUẢNG CÁO

3. Luyện tập Bài 1 Chương 1 Hình học 7

Qua bài giảng Hai góc đối đỉnhnày, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :

• Định nghĩa và tính chất hai góc đối đỉnh

3.1. Trắc nghiệm về Hai góc đối đỉnh

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Hình học 7 Bài 1 cực hay có đáp án và lời giải chi tiết.

• Câu 1:

  Hai góc đối đỉnh là hai góc có:

  • A. 1 cạnh của góc này là tia đối của 1 cạnh của góc
  • B. mỗi cạnh của góc này là tia đối của 1 cạnh của góc kia
  • C. tổng của hai góc bằng 1800
  • D. Số đo của chúng bằng nhau

• Câu 2:

  Hai góc đối đỉnh thì:

  • A. bằng nhau
  • B. bù nhau
  • C. kề, bù nhau
  • D. cả 3 câu trên đều sai

• Câu 3:

  Cho đường thẳng c cắt hai đường thẳng a, b thì:

  • A. hai góc đồng vị bằng nhau
  • B. hai góc trong cùng phía bù nhau
  • C. hai góc so le trong bằng nhau
  • D. cả 3 câu trên đêu sai

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

3.2. Bài tập SGK về Hai góc đối đỉnh

Các em có thể xem thêm phần hướng dẫn Giải bài tập Hình học 7 Bài 1 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Bài tập 1 trang 82 SGK Toán 7 Tập 1

Bài tập 2 trang 82 SGK Toán 7 Tập 1

Bài tập 3 trang 82 SGK Toán 7 Tập 1

Bài tập 4 trang 82 SGK Toán 7 Tập 1

Bài tập 5 trang 82 SGK Toán 7 Tập 1

Bài tập 6 trang 83 SGK Toán 7 Tập 1

Bài tập 7 trang 83 SGK Toán 7 Tập 1

Bài tập 8 trang 83 SGK Toán 7 Tập 1

Bài tập 9 trang 83 SGK Toán 7 Tập 1

Bài tập 10 trang 83 SGK Toán 7 Tập 1

Bài tập 1 trang 99 SBT Toán 7 Tập 1

Bài tập 2 trang 99 SBT Toán 7 Tập 1

Bài tập 3 trang 100 SBT Toán 7 Tập 1

Bài tập 4 trang 100 SBT Toán 7 Tập 1

Bài tập 5 trang 100 SBT Toán 7 Tập 1

Bài tập 6 trang 100 SBT Toán 7 Tập 1

Bài tập 7 trang 100 SBT Toán 7 Tập 1

Bài tập 1.1 trang 100 SBT Toán 7 Tập 1

Bài tập 1.2 trang 101 SBT Toán 7 Tập 1

Bài tập 1.3 trang 101 SBT Toán 7 Tập 1

Bài tập 1.4 trang 101 SBT Toán 7 Tập 1

4. Hỏi đáp Bài 1 Chương 1 Hình học 7

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!

-- Mod Toán Học 7 HỌC247

NONE

Bài học cùng chương

Hình học 7 Bài 2: Hai đường thẳng vuông góc Hình học 7 Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng Hình học 7 Bài 4: Hai đường thẳng song song Hình học 7 Bài 5: Tiên đề Ơ-clit về đường thẳng song song Hình học 7 Bài 6: Từ vuông góc đến song song Hình học 7 Bài 7: Định lí ADSENSE ADMICRO Bộ đề thi nổi bật UREKA AANETWORK

XEM NHANH CHƯƠNG TRÌNH LỚP 7

Toán 7

Toán 7 Kết Nối Tri Thức

Toán 7 Chân Trời Sáng Tạo

Toán 7 Cánh Diều

Giải bài tập Toán 7 KNTT

Giải bài tập Toán 7 CTST

Giải bài tập Toán 7 Cánh Diều

Trắc nghiệm Toán 7

Ngữ văn 7

Ngữ Văn 7 Kết Nối Tri Thức

Ngữ Văn 7 Chân Trời Sáng Tạo

Ngữ Văn 7 Cánh Diều

Soạn Văn 7 Kết Nối Tri Thức

Soạn Văn 7 Chân Trời Sáng Tạo

Soạn Văn 7 Cánh Diều

Văn mẫu 7

Tiếng Anh 7

Tiếng Anh 7 Kết Nối Tri Thức

Tiếng Anh 7 Chân Trời Sáng Tạo

Tiếng Anh 7 Cánh Diều

Trắc nghiệm Tiếng Anh 7 KNTT

Trắc nghiệm Tiếng Anh 7 CTST

Trắc nghiệm Tiếng Anh 7 Cánh Diều

Giải Sách bài tập Tiếng Anh 7

Khoa học tự nhiên 7

Khoa học tự nhiên 7 KNTT

Khoa học tự nhiên 7 CTST

Khoa học tự nhiên 7 Cánh Diều

Giải bài tập KHTN 7 KNTT

Giải bài tập KHTN 7 CTST

Giải bài tập KHTN 7 Cánh Diều

Trắc nghiệm Khoa học tự nhiên 7

Lịch sử và Địa lý 7

Lịch sử & Địa lí 7 KNTT

Lịch sử & Địa lí 7 CTST

Lịch sử & Địa lí 7 Cánh Diều

Giải bài tập LS và ĐL 7 KNTT

Giải bài tập LS và ĐL 7 CTST

Giải bài tập LS và ĐL 7 Cánh Diều

Trắc nghiệm Lịch sử và Địa lí 7

GDCD 7

GDCD 7 Kết Nối Tri Thức

GDCD 7 Chân Trời Sáng Tạo

GDCD 7 Cánh Diều

Giải bài tập GDCD 7 KNTT

Giải bài tập GDCD 7 CTST

Giải bài tập GDCD 7 Cánh Diều

Trắc nghiệm GDCD 7

Công nghệ 7

Công nghệ 7 Kết Nối Tri Thức

Công nghệ 7 Chân Trời Sáng Tạo

Công nghệ 7 Cánh Diều

Giải bài tập Công nghệ 7 KNTT

Giải bài tập Công nghệ 7 CTST

Giải bài tập Công nghệ 7 Cánh Diều

Trắc nghiệm Công nghệ 7

Tin học 7

Tin học 7 Kết Nối Tri Thức

Tin học 7 Chân Trời Sáng Tạo

Tin học 7 Cánh Diều

Giải bài tập Tin học 7 KNTT

Giải bài tập Tin học 7 CTST

Giải bài tập Tin học 7 Cánh Diều

Trắc nghiệm Tin học 7

Cộng đồng

Hỏi đáp lớp 7

Tư liệu lớp 7

Xem nhiều nhất tuần

Video Toán nâng cao lớp 7

Đề cương HK1 lớp 7

Con chim chiền chiện - Huy Cận - Ngữ văn 7 Chân Trời Sáng Tạo

Tiếng gà trưa - Xuân Quỳnh - Ngữ văn 7 Cánh Diều

Quê hương - Tế Hanh - Ngữ văn 7 Kết Nối Tri Thức

Toán 7 KNTT Bài 1: Tập hợp các số hữu tỉ

Toán 7 CTST Bài 2: Các phép tính với số hữu tỉ

Toán 7 Cánh diều Bài tập cuối chương 1

YOMEDIA YOMEDIA ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Bỏ qua Đăng nhập ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Đồng ý ATNETWORK ON QC Bỏ qua >>