Hỗn Số Là Gì? Cách Cộng Trừ Hỗn Số? Cách Tính Nhanh Hỗn Số?

Hỗn số là gì? Cách cộng trừ hỗn số? Cách tính nhanh hỗn số?Hỗn số lớp 5, 6 Tải về Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi. Mua ngay Từ 79.000đ Tìm hiểu thêm

Định nghĩa hỗn số là gì? Cấu tạo của hỗn số là gì? Cách cộng hỗn số như nào? Cách tính nhanh hỗn số? Mối liên hệ giữa phân số và hỗn số ra sao?… VnDoc.com tổng hợp cho tiết cho các em học sinh tham khảo.

Cách cộng trừ hỗn số? Cách tính nhanh hỗn số?

• 1. Định nghĩa hỗn số là gì?
• 2. Cách đổi hỗn số thành phân số
• 3. Các dạng toán về hỗn số
  • 3.1 Cách cộng hỗn số
  • 3.2 Cách trừ hỗn số
  • 3.3 Cách nhân chia hỗn số
  • 3.4 Tính giá trị của biểu thức
  • 3.5 Viết phân số dưới dạng hỗn số
  • 3.6. So sánh hỗn số
• 4. Cách tính nhanh hỗn số
• 5. Bài tập về Hỗn số

1. Định nghĩa hỗn số là gì?

• Hỗn số là kết quả của việc viết gọn tổng của một số tự nhiên nguyên dương với một phân số dương bằng cách bỏ dấu cộng xen giữa chúng. Như vậy, một hỗn số gồm hai phần: phần nguyên và phần phân số.
• Số đối của hỗn số này cũng được gọi là một hỗn số.
• Hỗn số được viết dưới dạng \(a\frac{b}{c}\). Phần phân số của hỗn số luôn luôn nhỏ hơn 1.

\(a+\frac{b}{c}=a\frac{b}{c}\)

Ví dụ:

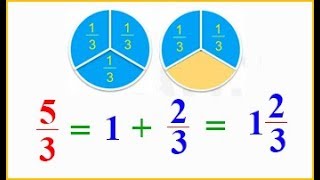
+ Cách đọc, viết hỗn số: Để đọc (hoặc viết) hỗn số, ta đọc (hoặc viết) phần nguyên trước rồi đọc (hoặc viết) phần phân số sau.

Ví dụ: Hỗn số \(5\frac{7}{{10}}\) có:

• Phần nguyên của hỗn số là 5 và phần phân số là \(\frac{7}{{10}}\).
• Hỗn số được đọc là “năm và bảy phần mười”

2. Cách đổi hỗn số thành phân số

\(a\frac{b}{c}=\frac{ac+b}{c}\)

Đổi phân số hoặc hỗn số dương

• Nếu phân số dương lớn hơn 1, ta có thể viết nó dưới dạng hỗn số bằng cách: chia tử cho mẫu. Thương tìm được là phần nguyên của hỗn số, phần phân số có tử là số dư là tử, còn mẫu vẫn là mẫu đã cho.
• Nếu muốn đổi một hỗn số dương dưới dạng một phân số, thực hiện nhân phần số nguyên với mẫu rồi cộng với tử, kết quả tìm được là tử của phân số, còn mẫu vẫn là mẫu đã cho.

Đổi phân số hoặc hỗn số âm

• Khi viết một phân số âm dưới dạng hỗn số, ta chỉ cần viết số đối của nó dưới dạng hỗn số rồi đặt dấu trước kết quả nhận được.
• Tương tự như vậy, khi viết một hỗn số âm dưới dạng phân số, chỉ cần viết số đối của nó dưới dạng phân số rồi đặt dấu “-“ trước kết quả.

3. Các dạng toán về hỗn số

3.1 Cách cộng hỗn số

Phương pháp giải:

Khi cộng hai hỗn số: có thể viết chúng dưới dạng phân số rồi thực hiện phép cộng phân số. Ta cũng có thể cộng phần nguyên với nhau, cộng phần phân số với nhau (khi hai hỗn số đều dương).

Ví dụ:

\(2\frac{1}{2}+3\frac{1}{4}=(2+3)+(\frac{1}{2}+\frac{1}{4})=5+\frac{3}{4}=5\frac{3}{4}\)

3.2 Cách trừ hỗn số

Phương pháp giải:

• Khi trừ hai hỗn số: có thể viết chúng dưới dạng phân số rồi thực hiện phép trừ phân số. Ta cũng có thể lấy phần nguyên của số bị trừ trừ phần nguyên của số trừ, phần phân số của số bị trừ trừ phần phân số của số trừ, rồi cộng hai kết quả với nhau (khi hai hỗn số đều dương, số bị trừ lớn hơn hoặc bằng số trừ).
• Khi hai hỗn số đều dương, số bị trừ lớn hơn hoặc bằng số trừ, nhưng phần phân số của số bị trừ nhỏ hơn phần phân số của số trừ, phải thực rút một đơn vị ở phần nguyên của số bị trừ để thêm vào phần phân số, sau đó tiếp tục trừ như trên.

3.3 Cách nhân chia hỗn số

Phương pháp giải:

• Khi nhân hoặc chia một hỗn số với một số nguyên, có thể viết hỗn số dưới dạng tổng của một số nguyên và một phân số.

3.4 Tính giá trị của biểu thức

Phương pháp giải:

Để có thể tính giá trị của các biểu thức số cần chú ý:

• Thứ tự thực hiện các phép tính.
• Căn cứ vào đặc điểm của các biểu thức ta có thể áp dụng tính chất các phép tính và quy tắc dấu ngoặc.

3.5 Viết phân số dưới dạng hỗn số

Phương pháp giải:

Áp dụng quy tắc viết phân số dưới dạng hỗn số và quy tắc viết hỗn số dưới dạng

phân số.

Ví dụ: Viết các phân số sau dưới dạng hỗn số :

\(\frac{7}{3};\frac{-15}{11}\)

Cách giải:

\(\frac{7}{3}=2\frac{1}{3}\)

\(\frac{-15}{11}=-1\frac{4}{11}\)

Ví dụ: Viết các hỗn số sau dưới dạng phân số :

\(3\frac{2}{8};-2\frac{5}{13}\)

Cách giải:

\(3\frac{2}{8}=\frac{26}{8}\)

\(-2\frac{5}{13}=-\frac{31}{13}\)

3.6. So sánh hỗn số

Để so sánh hai hỗn số, ta có hai cách sau:

Cách 1: Chuyển hỗn số về phân số

Muốn so sánh hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi so sánh hai phân số vừa chuyển đổi.

Cách 2: So sánh phần nguyên và phần phân số

+ Hỗn số nào có phần nguyên lớn hơn thì hỗn số đó lớn hơn và ngược lại hỗn số nào có phần nguyên nhỏ hơn thì hỗn số đó bé hơn.

+ Nếu hỗn số có hai phần nguyên bằng nhau thì ta so sánh phần phân số, hỗn số nào có phần phân số lớn hơn thì hỗn số đó lớn hơn và ngược lại hỗn số nào có phần phân số bé hơn thì hỗn số đó bé hơn.

4. Cách tính nhanh hỗn số

Khi thực hiện cộng hai hỗn số\(2\frac{2}{3}; 3\frac{1}{5}\), ta có thể tính nhanh hơn bằng cách cộng phần nguyên với phần nguyên, phần phân số với phần phân số rồi cộng hai kết quả lại với nhau.

\(2\frac{2}{3}+3\frac{1}{5}=(3+2)+(\frac{2}{3}+\frac{1}{5})=5+\frac{13}{15}=5\frac{13}{15}\)

Mối liên hệ giữa phân số và hỗn số

- Chuyển hỗn số thành phân số

• Phân số được chuyển từ hỗn số có:
• Mẫu số bằng với mẫu số của phân số.
• Tử số bằng với mẫu số nhân phần nguyên cộng Tử số của phần phân số.

- Chuyển phân số thành hỗn số

• Khi phân số lớn hơn 1 (tử số lớn hơn mẫu số).
• Có thể thực hiện chuyển phân số đó về dạng hỗn số.

5. Bài tập về Hỗn số

• Bài tập Toán lớp 5: Hỗn số
• Bài tập nâng cao Toán lớp 5: Hỗn số
• Toán nâng cao lớp 5: Dạng phân số, hỗn số

Tham khảo thêm

• Giải Toán lớp 6 trang 6 tập 2 Kết nối tri thức

• Toán lớp 6 bài 6 Phép chia hết hai số nguyên. Quan hệ chia hết trong tập hợp số nguyên

• Giải Toán lớp 6 trang 8 tập 2 Kết nối tri thức

• Giải Toán lớp 6 trang 9 tập 2 Kết nối tri thức

• Giải Toán lớp 6 trang 5 tập 2 Kết nối tri thức

• Toán lớp 6 bài 23: Mở rộng phân số. Phân số bằng nhau

• Toán lớp 6 trang 108, 109 Luyện tập chung Kết nối tri thức

• Giải Toán lớp 6 trang 7 tập 2 Kết nối tri thức

• Phương pháp xác định một số chia hết cho 7

• Toán lớp 6 trang 110 Bài tập cuối chương 5 Kết nối tri thức