Khái Niệm, Tính Chất Và Cách Chứng Minh Tứ Giác Là Hình Vuông
Có thể bạn quan tâm
Hình vuông là một hình khá quen thuộc trong đời sống hằng ngày, chúng ta đã bắt gặp các đồ vật hình vuông từ lúc còn bé. Hình vuông tuy không còn lạ lẫm với học sinh lớp 8 nhưng lại gây khá nhiều khó khăn cho các bạn bởi nhiều lý thuyết và bài tập rất phức tạp. Hôm nay, Gia Sư Việt sẽ giải quyết tất cả vướng mắc về Hình vuông qua bài viết: Khái niệm, tính chất và cách chứng minh Tứ giác là Hình vuông, các bạn cùng theo dõi dưới đây nhé.
Mục lục
- I. Khái niệm về Hình vuông
- II. Tính chất của Hình vuông
- III. Cách chứng minh Tứ giác là Hình vuông
- Cách 1: Hình chữ nhật có 2 cạnh kề bằng nhau
- Cách 2: Hình chữ nhật có đường chéo là phân giác
- Cách 3: Hình thoi có 1 góc vuông
I. Khái niệm về Hình vuông
Hình vuông là Tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
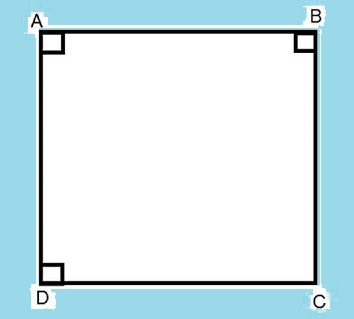
Từ khái niệm trên ta có:
Góc A = B = C = D = 90°
Cạnh AB = BC = CD = DA
II. Tính chất của Hình vuông
Hình vuông có tất cả các tính chất của Hình chữ nhật và Hình thoi.
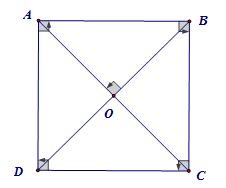
– Tính chất 1: Hình vuông có 2 cặp cạnh song song và bằng nhau
AB // và = CD
AD // và = BC
– Tính chất 2: Hai đường chéo bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.
Ví dụ: Hình vuông ABCD, AC cắt BD tại O, thì:
AC = BD
AC ⊥ BD
OA = OB = OC = OD
– Tính chất 3: Tâm của đường tròn nội tiếp và ngoại tiếp trùng nhau và là giao điểm của hai đường chéo của hình vuông.
Ví dụ: Hình vuông ABCD => O là tâm đường tròn nội tiếp và ngoại tiếp ABCD
III. Cách chứng minh Tứ giác là Hình vuông
Cách 1: Hình chữ nhật có 2 cạnh kề bằng nhau
Ví dụ: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC chúng cắt AB, AC theo thứ tự ở E và F. Tứ giác EFGH là hình gì? Vì sao?
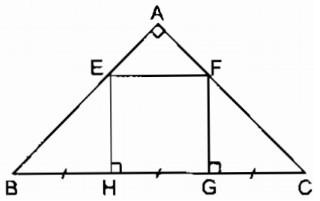
Theo bài ra, ta có:
ΔABC vuông cân tại A => Góc B = C = 45°
ΔBHE vuông tại H và có Góc B = 45° => ΔBHE vuông cân tại H => HB = HE
ΔCGF vuông tại G và có Góc C= 45° => ΔCGF vuông cân tại G => GC = GF
Mà BH = HG = GC (giả thiết) => HE = HG = GF
Lại có EH // GF (cùng vuông góc với BC) và EH = GF
=> Tứ giác HEFG là Hình bình hành ( Tứ giác có một cặp cạnh đối song song bằng nhau là Hình bình hành ).
Ngoài ra, Góc EHG = 90° nên HEFG là Hình chữ nhật, lại có EH = HG (chứng minh trên).
Vậy HEFG là Hình vuông ( Hình chữ nhật có 2 cạnh kề bằng nhau là Hình vuông ). ( đ.p.c.m)
Cách 2: Hình chữ nhật có đường chéo là phân giác
Ví dụ: Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N là chân đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông.
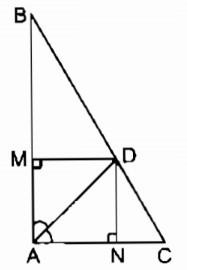
Xét tứ giác AMDN, ta có:
Góc MAN = 90° (giả thiết)
DM ⊥ AB (giả thiết) => Góc AMD = 90°
DN ⊥ AC (giả thiết) => Góc AND = 90°
Suy ra Tứ giác AMDN là Hình chữ nhật (tứ giác có ba góc vuông)
Lại có đường chéo AD là đường phân giác của A
Vậy Hình chữ nhật AMDN là Hình vuông
Cách 3: Hình thoi có 1 góc vuông
Ví dụ 1: Cho hình vuông ABCD. Trên AB, BC, CD, DA lấy theo thứ tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì? Vì sao?
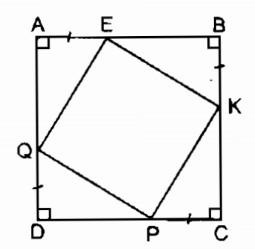
Ta có: AB = BC = CD = DA (gt)
AE = BK = CP = DQ (gt)
=> EB = KC = PD = QA
Xét ΔAEQ và ΔBKE, ta có:
AE = BK (gt)
A = B = 90°
QA = EB (chứng minh trên)
=> ΔAEQ = ΔBKE (c.g.c)
=> EQ = EK
Chứng minh tương tự, ta có: EK = KP, KP = PQ
Suy ra: EK = KP = PQ = EQ => Tứ giác EKPQ là Hình thoi. (1)
Mặt khác: ΔAEQ = ΔBKE
⇒ Góc AQE = BKE
Mà Góc AQE + AEQ = 90°
=> Góc BKE + AEQ = 90°
Lại có, Góc BKE + QEK + AEQ = 180°
Suy ra: Góc QEK = 180° – Góc BKE – Góc AEQ = 180° – 90° = 90° (2)
Từ (1) và (2) suy ra tứ giác EKPQ là Hình vuông ( Hình thoi có 1 góc vuông là Hình vuông. ( đ.p.c.m)
Ví dụ 2: Cho hình vuông DEBC. Trên cạnh DC lấy điểm A, trên tia đối của tia DC lấy điểm K, trên tia đối của tia ED lấy điểm M sao cho CA = DK = EM. Vẽ hình vuông DKIH (H thuộc cạnh DE). Chứng minh rằng ABMI là hình vuông.
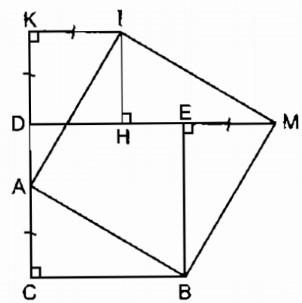
Xét ΔCAB và ΔEMB có:
CA = EM (gt) CB = EB Góc ACB = MEB = 90°
=> ΔCAB = ΔEMB (c.g.c)
=> AB = MB
Ta có: AK = DK+ DA
CD = CA + AD
Mà CA = DK nên AK = CD
Chứng minh tương tự, ta có: DE = HM, IM = MB
Suy ra: AM = BM = AI = IM
=> Tứ giác ABMI là Hình thoi.
Mặt khác, ta có ΔACB = ΔMEB (chứng minh trên)
=> Góc CBA = EBM
Mà Góc CBA + ABE = Góc CBE = 90°
Suy ra: Góc EBM + ABE = 90° hay Góc ABM = 90°
Vậy Tứ giác ABMI là Hình vuông ( Hình thoi có 1 góc vuông là hình vuông ) ( đ.p.c.m)
Lời kết: Qua bài viết này, Gia Sư Việt hi vọng giúp các bạn học sinh nắm chắc nhưng khái niệm, tính chất và cách chứng minh Tứ giác là Hình vuông. Chúng tôi tin rằng những bài tập phức tạp hay kì thi nâng cao cũng không thể làm khó các bạn nữa. Hãy luôn theo dõi nội dung cập nhật trên Website để tìm hiểu được nhiều bài học bổ ích nữa nhé, chúc các bạn học tập thật tốt và đạt kết quả cao.
Tham khảo thêm:
♦ Top 10 trung tâm cung cấp gia sư Toán giỏi nhất tại Hà Nội
♦ Tổng hợp kiến thức về các đường Đồng quy trong Tam giác
♦ Định nghĩa, tính chất & cách chứng minh các Tam giác đặc biệt
5 / 5 ( 2 bình chọn )Từ khóa » Cách Chứng Minh Hình Thoi Là Hình Vuông
-
Tính Chất, Dấu Hiệu Nhận Biết Và Cách Chứng Minh Hình Vuông Lớp 8
-
Hình Thoi Và Hình Vuông
-
HÌNH THOI – HÌNH VUÔNG - Học Để Thi
-
Dấu Hiệu Nhận Biết Hình Vuông - Giáo Viên Việt Nam
-
Dấu Hiệu Nhận Biết Hình Thoi, Hình Vuông, Hình Chữ Nhật, Hình Bình ...
-
Chứng Minh Hình Thoi Có Hai đường Chéo Bằng Nhau Là Hình Vuông?
-
Cách Chứng Minh Hình Thoi - Học Tốt
-
Cách Chứng Minh Tứ Giác Là Hình Vuông Hay, Chi Tiết - Toán Lớp 8
-
Chứng Minh Dấu Hiệu Nhận Biết Hình Vuông: Hình Chữ Nhật Có Hai ...
-
CHỨNG MINH CÁC DẤU HIỆU NHẬN BIẾT HÌNH VUÔNG
-
Chứng Minh Dấu Hiệu : Hình Thoi Có 1 Góc Vuông Là Hình Vuông - Olm
-
Chứng Minh Tứ Giác Là Hình Bình Hành, Hình Thoi, Hình Chữ Nhật, Hình ...
-
Cách Chứng Minh Hình Vuông - Xây Nhà