Lý Thuyết - Bài Tập Tam Giác đồng Dạng Lớp 8 Có Giải Chi Tiết - Icongchuc
Có thể bạn quan tâm
Bài tập tam giác đồng dạng lớp 8 có giải chi tiết.
Nội dung chính:
- Các trường hợp đồng dạng của tam giác thường
- Các trường hợp đồng dạng của tam giác vuông
- Tính chất tam giác đồng dạng là gì?
- Các phương pháp chứng minh hai tam giác đồng dạng toán lớp 8
- Trường hợp đồng dạng thứ nhất – Phiếu bài tập tam giác đồng dạng
- Trường hợp đồng dạng thứ hai
- Trường hợp đồng dạng thứ ba
- Trường hợp đồng dạng của tam giác vuông
- Bài tập tam giác đồng dạng tổng hợp
- Bài tập tam giác đồng dạng nâng cao
Các trường hợp đồng dạng của tam giác thường
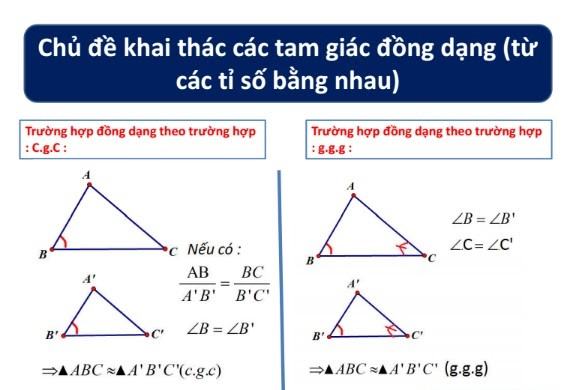
- Hai tam giác có ba cặp cạnh tương ứng tỷ lệ với nhau thì đồng dạng. (cạnh-cạnh-cạnh).
- Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng. (góc-góc).
- Hai tam giác có hai cặp cạnh tương ứng tỷ lệ với góc xen giữa hai cặp cạnh ấy bằng nhau thì đồng dạng. (cạnh-góc-cạnh).
Các trường hợp đồng dạng của tam giác vuông
Định lí 1 : Nếu cạnh huyền và cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng. Định lí 2 : Nếu hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng. (hai cạnh góc vuông) Định lí 3: Nếu góc nhọn của tam giác vuông này bằng góc nhọn của tam giác vuông kia thì hai tam giác đồng dạng. (góc)Tính chất tam giác đồng dạng là gì?
- Tỉ số hai đường phân giác, hai đường cao, hai đường trung tuyến, hai bán kính nội tiếp và ngoại tiếp, hai chu vi tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Tỉ số diện tích hai tam giác đồng dạng thì bằng bình phương tỉ số đồng dạng.
Các phương pháp chứng minh hai tam giác đồng dạng toán lớp 8
- Phương pháp 1: Hai tam giác được coi là đồng dạng nếu chúng có các cặp cạnh tương ứng tỉ lệ và các góc tương ứng tỉ lệ.
- Phương pháp 2: Định lý Talet: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó vạch ra trên cạnh đó những đoạn thẳng tương ứng tỷ lệ.
- Phương pháp 3: CM các điều kiện cần và đủ để hai tam giác đồng dạng: Hai tam giác có các cặp cạnh tương ứng tỷ lệ thì đồng dạng. Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng. Hai tam giác có hai cặp cạnh tương ứng tỷ lệ, hai góc xen giữa hai cặp cạnh ấy bằng nhau thì đồng dạng.
- Phương pháp 4: Chứng minh trường hợp 1 (cạnh-cạnh-cạnh): Nếu 3 cạnh của tam giác này tỷ lệ với 3 cạnh của tam giác kia thì 2 tam giác đó đồng dạng.
- Phương pháp 5: Chứng minh trường hợp 2 (cạnh-góc-cạnh): Nếu 2 cạnh của tam giác này tỷ lệ với 2 cạnh của tam giác kia và 2 góc tạo bởi tạo các cặp cạnh đó bằng nhau thì hai tam đó giác đồng dạng.
Trường hợp đồng dạng thứ nhất – Phiếu bài tập tam giác đồng dạng
Download [171.29 KB]
Trường hợp đồng dạng thứ hai
Download [232.79 KB]
Trường hợp đồng dạng thứ ba
Download [212.48 KB]
Trường hợp đồng dạng của tam giác vuông
Download [176.54 KB]
![]()
Bài tập tam giác đồng dạng tổng hợp
Download [26.24 KB]
Bài tập tam giác đồng dạng nâng cao
Download [22.89 KB]
Từ khóa » Bài Tập Tam Giác Vuông đồng Dạng
-
Chuyên đề Các Trường Hợp đồng Dạng Của Tam Giác Vuông
-
Bài Tập Các Trường Hợp đồng Dạng Của Tam Giác
-
Ba Dạng Bài Tập Các Trường Hợp đồng Dạng Của Tam Giác Vuông Có ...
-
Các Trường Hợp đồng Dạng Của Tam Giác Vuông
-
7.8. Các Trường Hợp đồng Dạng Của Tam Giác Vuông - Học Thật Tốt
-
Các Trường Hợp đồng Dạng Của Tam Giác Vuông – Toán Lớp 8
-
Các Trường Hợp đồng Dạng Của Tam Giác Vuông - Toán 8
-
Chứng Minh Hai Tam Giác Vuông đồng Dạng Hay, Chi Tiết - Toán Lớp 8
-
Giải Toán 8 Bài 8. Các Trường Hợp đồng Dạng Của Tam Giác Vuông
-
Bài Tập Các Trường Hợp đồng Dạng Của Tam Giác Vuông
-
[CHUẨN NHẤT] Các Trường Hợp đồng Dạng Của Tam Giác Vuông
-
Phiếu Bài Tập Tam Giác đồng Dạng Lớp 8 Có Giải Chi Tiết [word]
-
Các Trường Hợp đồng Dạng Của Tam Giác Vuông – Học Tốt Toán 8 - Itoan
-
Bài 8: Các Trường Hợp đồng Dạng Của Tam Giác Vuông – Luyện Tập ...